Effektivt designinsats, radera och medianfrågor på en uppsättning

Med tanke på en tom uppsättning initialt och ett antal frågor på den var och en av följande typer:
- Infoga 'X' görs med uppdatering (1 0 10^6 x 1). Observera att roten till trädet passeras startindex passeras som 0 och slutindex som 10^6 så att alla intervall som har x uppdateras.
- Radera 'X' görs med uppdatering (1 0 10^6 x -1). Observera att roten till trädet passeras startindex passeras som 0 och slutindex som 10^6 så att alla intervall som har x uppdateras.
Exempel:
Input : Insert 1 Insert 4 Insert 7 Median Output : The first three queries should insert 1 4 and 7 into an empty set. The fourth query should return 4 (median of 1 4 7).
För expository syfte antar vi följande men dessa antaganden är inte begränsningarna för metoden som diskuteras här:
1. När som helst är alla element distinkta som inte är någon av dem förekommer mer än en gång.
2. "Median" -frågan görs endast när det finns ett udda antal element i uppsättningen. (Vi kommer att behöva göra två frågor på vårt segmentträd i händelse av jämna nummer)
3. Elementen i uppsättningen sträcker sig från 1 till +10^6.
Metod 1 (naiv)
I naiv implementering kan vi göra de första två frågorna i O (1) men den sista frågan i O (max_elem) där max_elem är det maximala elementet i alla tider (inklusive borttagna element).
Låt oss anta en matris räkna[] (av storlek 10^6 + 1) För att upprätthålla räkningen för varje element i delmängden. Följande är enkla och självförklarande algoritmer för de 3 frågorna:
Infoga X -fråga:
count[x]++; if (x > max_elem) max_elem = x; n++;
Radera X -fråga:
if (count[x] > 0) count[x]--; n--;
Medianfråga:
sum = 0; i = 0; while( sum <= n / 2 ) { i++; sum += count[i]; } median = i; return median; Illustration av matrisräkning [] som representerar uppsättningen {1 4 7 8 9} Medianelementet är '7':

Den 'median' frågan avser att hitta (n + 1)/2: e '1' i matrisen i detta fall 3: e '1'; Nu gör vi samma sak med ett segmentträd.
Metod 2 (med hjälp av Segmentträd )
Vi gör en segmentträd För att lagra summan av intervaller där ett intervall [A B] representerar antalet element som finns i uppsättningen för närvarande i intervallet [A B]. Om vi till exempel överväger exemplet ovan (3 7) Returnerar 2 Query (4 4) returnerar 1 fråga (5 5) returnerar 0.
Infoga och radera frågor är enkla och båda kan implementeras med hjälp av funktionsuppdatering (int x int diff) (lägger till 'diff' vid index 'x')
Algoritm
// adds ‘diff’ at index ‘x’ update(node a b x diff) // If leaf node If a == b and a == x segmentTree[node] += diff // If non-leaf node and x lies in its range If x is in [a b] // Update children recursively update(2*node a (a + b)/2 x diff) update(2*node + 1 (a + b)/2 + 1 b x diff) // Update node segmentTree[node] = segmentTree[2 * node] + segmentTree[2 * node + 1]
Ovanstående rekursiv funktion körs i O (log (max_elem)) (I detta fall är max_elem 10^6) och används för både införande och borttagning med följande samtal:
Nu funktionen för att hitta indexet med kth '1' där 'k' i detta fall alltid kommer att vara (n + 1) / 2 detta kommer att fungera mycket som binär sökning Du kan tänka på det som en rekursiv binär sökfunktion på ett segmentträd.
Låt oss ta ett exempel för att förstå att vår uppsättning för närvarande har element {1 4 7 8 9} och representeras därför av följande segmentträd.
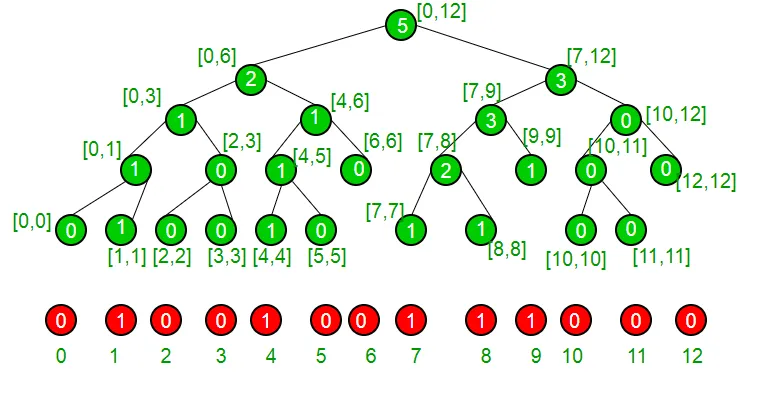
Om vi befinner oss på en icke-bladnod är vi säkra på att det har båda barnen vi ser om det vänstra barnet har mer eller lika antal av en som 'K' om ja, vi är säkra på att vårt index ligger i den vänstra undertråden annars om vänsterundertre har mindre antal 1 än k så är vi säkra på att vårt index ligger i höger undertree. Vi gör detta rekursivt för att nå vårt index och därifrån returnerar vi det.
Algoritm
1.findKth(node a b k) 2. If a != b 3. If segmentTree[ 2 * node ] >= k 4. return findKth(2*node a (a + b)/2 k) 5. else 6. return findKth(2*node + 1 (a + b)/2 + 1 b k - segmentTree[ 2 * node ]) 7. else 8. return a
Ovanstående rekursiv funktion körs i O (log (max_elem)) .
// A C++ program to implement insert delete and // median queries using segment tree #include #define maxn 3000005 #define max_elem 1000000 using namespace std ; // A global array to store segment tree. // Note: Since it is global all elements are 0. int segmentTree [ maxn ]; // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. void update ( int node int a int b int x int diff ) { // If current node is a leaf node if ( a == b && a == x ) { // add 'diff' and return segmentTree [ node ] += diff ; return ; } // If current node is non-leaf and 'x' is in its // range if ( x >= a && x <= b ) { // update both sub-trees left and right update ( node * 2 a ( a + b ) / 2 x diff ); update ( node * 2 + 1 ( a + b ) / 2 + 1 b x diff ); // Finally update current node segmentTree [ node ] = segmentTree [ node * 2 ] + segmentTree [ node * 2 + 1 ]; } } // Returns k'th node in segment tree int findKth ( int node int a int b int k ) { // non-leaf node will definitely have both // children; left and right if ( a != b ) { // If kth element lies in the left subtree if ( segmentTree [ node * 2 ] >= k ) return findKth ( node * 2 a ( a + b ) / 2 k ); // If kth one lies in the right subtree return findKth ( node * 2 + 1 ( a + b ) / 2 + 1 b k - segmentTree [ node * 2 ]); } // if at a leaf node return the index it stores // information about return ( segmentTree [ node ]) ? a : -1 ; } // insert x in the set void insert ( int x ) { update ( 1 0 max_elem x 1 ); } // delete x from the set void delete ( int x ) { update ( 1 0 max_elem x -1 ); } // returns median element of the set with odd // cardinality only int median () { int k = ( segmentTree [ 1 ] + 1 ) / 2 ; return findKth ( 1 0 max_elem k ); } // Driver code int main () { insert ( 1 ); insert ( 4 ); insert ( 7 ); cout < < 'Median for the set {147} = ' < < median () < < endl ; insert ( 8 ); insert ( 9 ); cout < < 'Median for the set {14789} = ' < < median () < < endl ; delete ( 1 ); delete ( 8 ); cout < < 'Median for the set {479} = ' < < median () < < endl ; return 0 ; }
Java // A Java program to implement insert delete and // median queries using segment tree import java.io.* ; class GFG { public static int maxn = 3000005 ; public static int max_elem = 1000000 ; // A global array to store segment tree. // Note: Since it is global all elements are 0. public static int [] segmentTree = new int [ maxn ] ; // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. public static void update ( int node int a int b int x int diff ) { // If current node is a leaf node if ( a == b && a == x ) { // Add 'diff' and return segmentTree [ node ] += diff ; return ; } // If current node is non-leaf and 'x' // is in its range if ( x >= a && x <= b ) { // Update both sub-trees left and right update ( node * 2 a ( a + b ) / 2 x diff ); update ( node * 2 + 1 ( a + b ) / 2 + 1 b x diff ); // Finally update current node segmentTree [ node ] = segmentTree [ node * 2 ] + segmentTree [ node * 2 + 1 ] ; } } // Returns k'th node in segment tree public static int findKth ( int node int a int b int k ) { // Non-leaf node will definitely have both // children; left and right if ( a != b ) { // If kth element lies in the left subtree if ( segmentTree [ node * 2 ] >= k ) { return findKth ( node * 2 a ( a + b ) / 2 k ); } // If kth one lies in the right subtree return findKth ( node * 2 + 1 ( a + b ) / 2 + 1 b k - segmentTree [ node * 2 ] ); } // If at a leaf node return the index it stores // information about return ( segmentTree [ node ] != 0 ) ? a : - 1 ; } // Insert x in the set public static void insert ( int x ) { update ( 1 0 max_elem x 1 ); } // Delete x from the set public static void delete ( int x ) { update ( 1 0 max_elem x - 1 ); } // Returns median element of the set // with odd cardinality only public static int median () { int k = ( segmentTree [ 1 ] + 1 ) / 2 ; return findKth ( 1 0 max_elem k ); } // Driver code public static void main ( String [] args ) { insert ( 1 ); insert ( 4 ); insert ( 7 ); System . out . println ( 'Median for the set {147} = ' + median ()); insert ( 8 ); insert ( 9 ); System . out . println ( 'Median for the set {14789} = ' + median ()); delete ( 1 ); delete ( 8 ); System . out . println ( 'Median for the set {479} = ' + median ()); } } // This code is contributed by avanitrachhadiya2155
Python3 # A Python3 program to implement insert delete and # median queries using segment tree maxn = 3000005 max_elem = 1000000 # A global array to store segment tree. # Note: Since it is global all elements are 0. segmentTree = [ 0 for i in range ( maxn )] # Update 'node' and its children in segment tree. # Here 'node' is index in segmentTree[] 'a' and # 'b' are starting and ending indexes of range stored # in current node. # 'diff' is the value to be added to value 'x'. def update ( node a b x diff ): global segmentTree # If current node is a leaf node if ( a == b and a == x ): # add 'diff' and return segmentTree [ node ] += diff return # If current node is non-leaf and 'x' is in its # range if ( x >= a and x <= b ): # update both sub-trees left and right update ( node * 2 a ( a + b ) // 2 x diff ) update ( node * 2 + 1 ( a + b ) // 2 + 1 b x diff ) # Finally update current node segmentTree [ node ] = segmentTree [ node * 2 ] + segmentTree [ node * 2 + 1 ] # Returns k'th node in segment tree def findKth ( node a b k ): global segmentTree # non-leaf node will definitely have both # children left and right if ( a != b ): # If kth element lies in the left subtree if ( segmentTree [ node * 2 ] >= k ): return findKth ( node * 2 a ( a + b ) // 2 k ) # If kth one lies in the right subtree return findKth ( node * 2 + 1 ( a + b ) // 2 + 1 b k - segmentTree [ node * 2 ]) # if at a leaf node return the index it stores # information about return a if ( segmentTree [ node ]) else - 1 # insert x in the set def insert ( x ): update ( 1 0 max_elem x 1 ) # delete x from the set def delete ( x ): update ( 1 0 max_elem x - 1 ) # returns median element of the set with odd # cardinality only def median (): k = ( segmentTree [ 1 ] + 1 ) // 2 return findKth ( 1 0 max_elem k ) # Driver code if __name__ == '__main__' : insert ( 1 ) insert ( 4 ) insert ( 7 ) print ( 'Median for the set {147} =' median ()) insert ( 8 ) insert ( 9 ) print ( 'Median for the set {14789} =' median ()) delete ( 1 ) delete ( 8 ) print ( 'Median for the set {479} =' median ()) # This code is contributed by mohit kumar 29
C# // A C# program to implement insert delete // and median queries using segment tree using System ; class GFG { public static int maxn = 3000005 ; public static int max_elem = 1000000 ; // A global array to store segment tree. // Note: Since it is global all elements are 0. public static int [] segmentTree = new int [ maxn ]; // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. public static void update ( int node int a int b int x int diff ) { // If current node is a leaf node if ( a == b && a == x ) { // Add 'diff' and return segmentTree [ node ] += diff ; return ; } // If current node is non-leaf and 'x' // is in its range if ( x >= a && x <= b ) { // Update both sub-trees left and right update ( node * 2 a ( a + b ) / 2 x diff ); update ( node * 2 + 1 ( a + b ) / 2 + 1 b x diff ); // Finally update current node segmentTree [ node ] = segmentTree [ node * 2 ] + segmentTree [ node * 2 + 1 ]; } } // Returns k'th node in segment tree public static int findKth ( int node int a int b int k ) { // Non-leaf node will definitely have both // children; left and right if ( a != b ) { // If kth element lies in the left subtree if ( segmentTree [ node * 2 ] >= k ) { return findKth ( node * 2 a ( a + b ) / 2 k ); } // If kth one lies in the right subtree return findKth ( node * 2 + 1 ( a + b ) / 2 + 1 b k - segmentTree [ node * 2 ]); } // If at a leaf node return the index it // stores information about if ( segmentTree [ node ] != 0 ) { return a ; } else { return - 1 ; } } // Insert x in the set public static void insert ( int x ) { update ( 1 0 max_elem x 1 ); } // Delete x from the set public static void delete ( int x ) { update ( 1 0 max_elem x - 1 ); } // Returns median element of the set // with odd cardinality only public static int median () { int k = ( segmentTree [ 1 ] + 1 ) / 2 ; return findKth ( 1 0 max_elem k ); } // Driver code static public void Main () { insert ( 1 ); insert ( 4 ); insert ( 7 ); Console . WriteLine ( 'Median for the set {147} = ' + median ()); insert ( 8 ); insert ( 9 ); Console . WriteLine ( 'Median for the set {14789} = ' + median ()); delete ( 1 ); delete ( 8 ); Console . WriteLine ( 'Median for the set {479} = ' + median ()); } } // This code is contributed by rag2127
JavaScript < script > // A Javascript program to implement insert delete and // median queries using segment tree let maxn = 3000005 ; let max_elem = 1000000 ; // A global array to store segment tree. // Note: Since it is global all elements are 0. let segmentTree = new Array ( maxn ); for ( let i = 0 ; i < maxn ; i ++ ) { segmentTree [ i ] = 0 ; } // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. function update ( node a b x diff ) { // If current node is a leaf node if ( a == b && a == x ) { // Add 'diff' and return segmentTree [ node ] += diff ; return ; } // If current node is non-leaf and 'x' // is in its range if ( x >= a && x <= b ) { // Update both sub-trees left and right update ( node * 2 a Math . floor (( a + b ) / 2 ) x diff ); update ( node * 2 + 1 Math . floor (( a + b ) / 2 ) + 1 b x diff ); // Finally update current node segmentTree [ node ] = segmentTree [ node * 2 ] + segmentTree [ node * 2 + 1 ]; } } // Returns k'th node in segment tree function findKth ( node a b k ) { // Non-leaf node will definitely have both // children; left and right if ( a != b ) { // If kth element lies in the left subtree if ( segmentTree [ node * 2 ] >= k ) { return findKth ( node * 2 a Math . floor (( a + b ) / 2 ) k ); } // If kth one lies in the right subtree return findKth ( node * 2 + 1 Math . floor (( a + b ) / 2 ) + 1 b k - segmentTree [ node * 2 ]); } // If at a leaf node return the index it stores // information about return ( segmentTree [ node ] != 0 ) ? a : - 1 ; } // Insert x in the set function insert ( x ) { update ( 1 0 max_elem x 1 ); } // Delete x from the set function delet ( x ) { update ( 1 0 max_elem x - 1 ); } // Returns median element of the set // with odd cardinality only function median () { let k = ( segmentTree [ 1 ] + 1 ) / 2 ; return findKth ( 1 0 max_elem k ); } // Driver code insert ( 1 ); insert ( 4 ); insert ( 7 ); document . write ( 'Median for the set {147} = ' + median () + '
' ); insert ( 8 ); insert ( 9 ); document . write ( 'Median for the set {14789} = ' + median () + '
' ); delet ( 1 ); delet ( 8 ); document . write ( 'Median for the set {479} = ' + median () + '
' ); // This code is contributed by unknown2108 < /script>
Produktion:
Median for the set {147} = 4 Median for the set {14789} = 7 Median for the set {479} = 7
Slutsats:
Alla tre frågor körs in O (log (max_elem)) I detta fall är max_elem = 10^6 så log (max_elem) ungefär lika med 20.
Segmentträdet använder O (max_elem) utrymme.
Om det inte fanns borttagningsfrågan kunde problemet också ha gjorts med en berömd algoritm här .