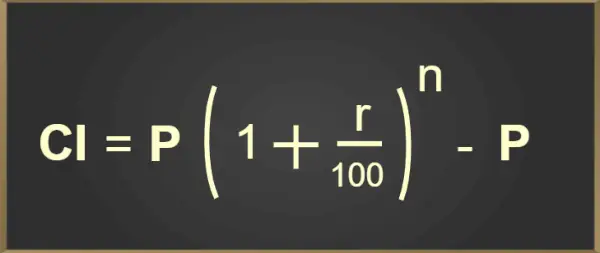
Sammansatt ränta är den ränta som beräknas mot ett låne- eller inlåningsbelopp där ränta beräknas på kapitalbeloppet samt den tidigare intjänade räntan.

Den gemensamma skillnaden mellan sammansatt och enkel ränta är att i ränta på ränta , beräknas ränta för kapitalbeloppet såväl som för den tidigare intjänade räntan medan enkel ränta endast beror på den investerade kapitalet.

Innehållsförteckning

• Vad är sammansatt ränta?
• Formel med sammansatt ränta
• Hur beräknar man ränta?
• Sammansatt ränta Formel – Derivation
• Halvårsformel med sammansatt ränta
• Kvartalsvis sammansatt ränta formel
• Formel för månatlig ränta
• Daglig sammansatt ränta formel
• Formel för periodisk sammansättningshastighet
• Regel av 72
• Sammansatt ränta för på varandra följande år
• Formel för kontinuerligt sammansatt intresse
• Några andra tillämpningar av sammansatt ränta
• Skillnaden mellan sammansatt ränta och enkel ränta
• Exempel på sammansatt ränta
• Sammansatt ränta – övningsfrågor

Vad är sammansatt ränta?

Sammansatt ränta är ränta på kapitalbeloppet såväl som den ränta som intjänats på kapitalbeloppet. Ordet sammansatt ränta är sammansatt av två ord Sammansättning som betyder sammansatt av två eller flera och Ränta betyder pengar som tjänats in på att låna ut beloppet. Därför är sammansatt ränta pengarna som tjänas på utlåning och den är sammansatt av två typer av räntor som är:

• Ränta på kapitalbelopp

• Ränta på ränta intjänad på kapitalbelopp under perioden

Sammansatt ränta Definition

Ränta på ränta är den ränta som beräknas på kapitalbeloppet och den ränta som intjänats tidigare. Det betecknas av C.I. Det är mycket användbart för investeringar och återbetalning av lån. Det är också känt som ränta på ränta.

Ränta på ränta är mycket användbar inom bank- och finanssektorerna och är också användbar inom andra sektorer. Några av dess användning är:

• Tillväxt av befolkningen i ett land
• Värdet av investeringen över en tidsperiod.
• För att hitta uppblåsta kostnader och det avskrivna värdet på en artikel.
• För att förutsäga tillväxten för alla institutioner eller länder.

Sammansatt ränta (C.I) = Belopp – Kapital

Formel med sammansatt ränta

Ränta på ränta beräknas, efter beräkning av det totala beloppet över en tidsperiod, baserat på räntesatsen och den ursprungliga kapitalbeloppet. För en initial kapital på P, räntesats per år av r, tidsperiod t i år, frekvensen av antalet gånger räntan sammansätts årligen n, formeln för beräkning av CI är följande:

CI = P(1 + r/100) ⁿ – P

Ovanstående formel för beräkning av sammansatt ränta läggs till i bildformuläret nedan:

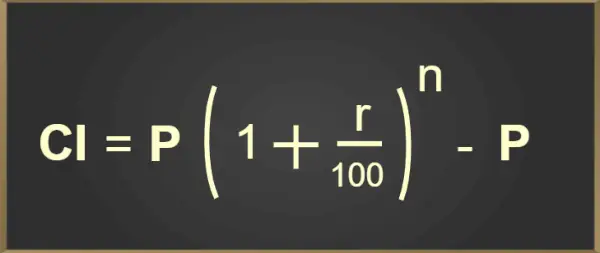
Formel med sammansatt ränta

Var,

• P = Main
• r = Räntesats
• n = Antal gånger ränta är sammansatt per år
• t = Tid (i år)

Vi kan skriva formeln för sammansatt ränta som:

Sammansatt ränta = A – P

Var,

• A = Totalt belopp efter sammansättning
• P = Initialt huvudbelopp

Sammansatt ränta = P(1 + r/n) ^nt -P

Var,

• P = Initialt huvudbelopp
• r = Årlig ränta
• n = Antal gånger ränta är sammansatt
• t = Antal år

Sammansatt ränta kan beräknas årligen, halvårsvis, kvartalsvis, månadsvis, dagligen, etc. enligt kravet.

Hur beräknar man ränta?

Ränta på ränta är den ränta som betalas både på kapitalbelopp och ackumulerad ränta. Räntan som tjänas in vid varje intervall läggs till den initiala huvudannonsen så att kapitalbeloppet fortsätter att öka.

Använd följande metoder för att hitta sammansatt ränta.

Steg 1: Anteckning, huvudman, taxa och tidsperiod

Steg 2: Beräkna mängden med formeln A = P(1 + r/100) ⁿ

Steg 3: Hitta sammansatt ränta med formeln CI = Belopp – Huvudstol

Med jämna mellanrum klubbas den hittills ackumulerade räntan med det befintliga kapitalbeloppet och sedan är räntan beräknas för den nya huvudmannen . Den nya kapitalbeloppet är lika med summan av den initiala kapitalbeloppet och den ränta som hittills ackumulerats.

Sammansatt ränta = ränta på huvudstolen + ränta på huvudmannens ränta (från andra året och därefter)

Sammansatt ränta beräknas med regelbundna intervall som årligen (årlig), halvårsvis, kvartalsvis, månadsvis, etc; Det är som att återinvestera ränteintäkterna från en investering gör att pengarna växer snabbare över tiden! Det är precis vad sammansatt ränta gör med pengar. Banker eller någon finansiell organisation beräknar beloppet endast baserat på sammansatt ränta.

Sammansatt ränta Formel – Derivation

Sammansatt ränta formel är ett kraftfullt verktyg som används inom finans för att beräkna den ränta som tjänas in eller betalas på ett initialt kapitalbelopp, som inkluderar både den initiala kapitalbeloppet och den ränta som ackumulerats under tidigare perioder. Formeln för sammansatt ränta ges av:

Var,

• A är det framtida värdet av investeringar eller lån, inklusive ränta
• P är huvudbelopp (initial investering eller lånebelopp)
• r är årlig räntesats (som en decimal)
• n är Antalet gånger som räntan höjs per år
• Det är Tid Pengar investeras eller lånas för, i år

Enkel intresseformel

Enkel ränta beräknas endast på kapitalbeloppet. Det kan representeras av formeln ,

Sammansatt ränta formel med kontinuerlig sammansättning

När ränta sammansätts kontinuerligt (oändligt många gånger per år), härleds formeln för sammansatt ränta med formeln för kontinuerlig sammansättning:

Var,

• e är Eulers nummer (ungefär 2,71828)
• P är huvudbelopp
• r är den årliga räntesatsen
• det är tid i år

Generell formel för sammansatt ränta

För att härleda den allmänna formeln för sammansatt ränta, låt oss överväga att sammansätta räntan n gånger per år.

Om P sammansätts n gånger per år med en årlig ränta r, räntan r divideras med n och tillämpas n gånger per år. Så efter t år blir formeln:

Var,

• representerar räntan per sammansättningsperiod.
• nt är det totala antalet sammansättningsperioder under t år.

Detta formeln illustrerar hur det initiala kapitalbeloppet växer över tiden när räntan höjs med jämna mellanrum . När n närmar sig oändligheten (dvs kontinuerlig sammansättning) konvergerar formeln mot den kontinuerliga sammansättningsformeln .

Sammanfattningsvis, formeln för sammansatt ränta är ett resultat av den kontinuerliga blandningsformeln anpassad för diskreta blandningsperioder per år. Det möjliggör beräkning av det framtida värdet av en investering eller ett lån, med hänsyn tagen till sammansatt ränta med jämna mellanrum.

Halvårsformel med sammansatt ränta

Låt den investerade kapitalet vara P och räntan är R % per år som kompounderas halvårsvis för 't' år

Som den läggs samman halvårsvis, huvudstolen kommer att ändras i slutet av 6 månader, och ränta som intjänats fram till dess kommer att läggas till kapitalbeloppet och då blir detta den nya kapitalbeloppet. På samma sätt beräknas det slutliga beloppet.

Vi vet,

sats = R% per år Sammansatt halvårsvis

hastighet = (R/2) %

tid är t år vi vet att t år har 2t halvår.

Nu,

A = P (1 + R/200) ^2t

CI = A – P

Kvartalsvis sammansatt ränta formel

Låt det investerade kapitalet vara P och räntan är R % per år som kompounderas kvartalsvis under t år.

Som den läggs samman kvartalsvis, huvudbeloppet kommer att ändras i slutet av 3 månader, och ränta som intjänats dittills kommer att läggas till kapitalbeloppet och då blir detta den nya kapitalbeloppet. På samma sätt beräknas det slutliga beloppet.

vi vet,

ränta = R% per år sammansatt kvartalsvis

rate = (R/4)%

tid är t år vi vet att t år har 4t kvartal.

Nu,

A = P(1 + R/400) ^4t

CI = A – P

Kolla upp: Kvartalsvis sammansatt ränta formel

Formel för månatlig ränta

Om räntan ackumuleras månadsvis blir antalet kompounderingstillfällen 12 och räntan varje månad blir 1/12 av årlig ränta. Följaktligen ges Formel för månadssammansatt ränta som

A = P[1 + (R/1200)] ^12t

CI = A – P

Kolla upp: Formel med månatlig ränta

Daglig sammansatt ränta formel

Om räntan höjs dagligen, alltså.

Ny ränta kommer att vara R/365 %

n = 365

Därför ges formeln för daglig ränta som,

A = P[1 + (R/36500)] ^365t

CI = A – P

Formel för periodisk sammansättningshastighet

Totalt belopp, inklusive kapital P och sammansatt ränta CI, ges av:

A = P[1 + (r/n)] ^nt

var,

• P = Main
• A = Slutligt belopp
• r = Årlig ränta
• n = Antal gånger ränta är sammansatt
• t = Tid (i år)

Sålunda är sammansatt ränta:

CI = A – P

Regel av 72

Regel 72 är formeln som används för att uppskatta hur många år våra pengar fördubblas om de förenas årligen. För exempel , om våra pengar är investerade på r % Förvärras årligen så tar det 72/r år för våra pengar att fördubblas.

Denna beräkning är också användbar för att beräkna det uppblåsta värdet av våra pengar, d.v.s. det ger på hur många år värdet på vår tillgång halveras om den skrivs av årligen.

Regel av 72 formel

Följande formel används för att uppskatta antalet år för att vår investering ska fördubblas.

N = 72/r

var,

• N är ungefärligt antal år Våra pengar fördubblas
• r är den kurs som våra pengar sammansätts med årligen

Exempel på regel 72

Antag att Kabir har investerat 10 00 000 rupier i en skuldfond som ger en avkastning på 8 %. Ta reda på hur många år dess pengar fördubblas om de förstärks årligen.

Med formeln ovan: N = 72/8 = 9 år

Således, det tar 9 år för Kabirs pengar att fördubblas.

Sammansatt ränta för på varandra följande år

Om vi ​​har samma summa och samma ränta. C.I. för ett visst år är alltid mer än C.I för föregående år. (CI för 3:e året är större än CI för 2:a året). Skillnaden mellan CI för två på varandra följande år är en ränta på ett år på C.I föregående år.

C.I för 3:a året – C.I av 2:a året = C.I av 2:a året × r × 1/100

Skillnaden mellan belopp för två på varandra följande år är räntan på ett år på föregående års belopp.

Mängd 3:a året – Mängd 2:a året = Mängd 2:a året × r × 1/100

Nyckelresultat

När vi har samma summa och samma takt ,

C.I för n:e året = C.I för (n – 1) år + ränta för ett år på C.I för (n – 1) år

Formel för kontinuerligt sammansatt intresse

Continuous Compounding Formula används inom finans för att beräkna det slutliga värdet av en investering som genomgår kontinuerlig kompoundering under olika perioder och värde läggs till över tiden. Formeln för kontinuerlig blandning ges som

Slutvärde = Nuvärde × e ^rt

var,

• r är räntan
• det är tid

Lär dig mer, Kontinuerlig sammansättningsformel

Några andra tillämpningar av sammansatt ränta

Tillväxt: Detta används främst för tillväxt om branscher är relaterade.

Produktion efter n år = initial produktion × (1 + r/100) ⁿ

Avskrivning: När kostnaden för en produkt minskar med r% varje år, är dess värde efter n år

Nuvärde × (1 + r/100) ⁿ

Befolkningsproblem: När befolkningen i en stad, stad eller by ökar i en viss takt per år.

Population efter n år = nuvarande befolkning × (1 + r/100) ⁿ

Skillnaden mellan sammansatt ränta och enkel ränta

Skillnaden mellan sammansatt ränta och enkel ränta kan du lära dig nedan i den här artikeln

Sammansatt ränta vs enkel ränta
Sammansatt ränta (CI)	Enkelt intresse (SI)
CI är ränta som beräknas både på kapitalbeloppet och den tidigare intjänade räntan.	SI är ränta som endast beräknas på kapitalbeloppet.
För samma princip, hastighet och tidsperiod CI> JA	För samma princip, hastighet och tidsperiod JA
Formel för CI är A = P(1 + R/100) T CI = A – P	Formel för SI är IF = (P×R×T) / 100

Exempel på sammansatt ränta

Några exempel på formler med sammansatt ränta är,

Exempel 1: Hitta den sammansatta räntan när kapitalbeloppet = 6000 Rs, räntan = 10 % per år och tiden = 2 år.

Lösning:

Ränta för första året = (6000 × 10 × 1)/100 = 600

Belopp i slutet av första året = 6000 + 600 = 6600

Ränta för andra året = (6600 × 10 × 1) / 100 = 660

Belopp i slutet av andra året = 6600 + 660 = 7260

Sammansatt ränta = 7260 – 6000 = 1260

Exempel 2: Vad blir den sammansatta räntan på Rs 8000 om två år när räntan är 2 % per år?

Lösning:

Given,

• Huvud-P = 8000
• Betyg r = 2 %
• Tid = 2 år

genom formel

A = P (1 + R/100) ⁿ

A = 8000 (1 + 2/100) ² = 8000 (102/100) ²

A = 8323

Sammansatt ränta = A – P = 8323 – 8000 = 323 Rs

Exempel 3: Hari deponerade Rs. 4000 med ett finansbolag i 2 år med en ränta på 5% per år. Vad är räntan som Rohit får efter 2 år?

Lösning:

Given,

• Huvud-P = 4000
• Betyg r = 5 %
• Tid = 2 år

Med formeln,

A = P (1 + R/100) ⁿ

A= 4000 (1 + 5/100) ²

A= 4000 (105/100) ²

A= 4410

Sammansatt ränta = A – P = 4410 – 4000 = 410

Exempel 4: Hitta den sammansatta räntan på Rs. 2000 med 4 % per år i 1,5 år. När räntan höjs halvårsvis?

Lösning:

Given,

• Huvudp = 2000
• Betyg r = 4 %
• Tid = 1,5 (dvs 3 halvår)

med formel,

A = P (1 + R/200) ²ⁿ

A = 2000 (1 + 4/200) ³

A = 2000 (204/200) ³

A = 2122

Sammansatt ränta = A – P = 2122 – 2000 = 122

Exempel 5: Vad är den sammansatta räntan på 10 000 för ett år med en ränta på 20 % per år, om räntan sammansätts kvartalsvis?

Lösning:

Given,

• Huvud P = 10 000 Rs
• Pris R = 12 % (12/4 = 3 % per kvartalsår)
• Tid = 1 år (1 × 4 = 4 kvartal)

Med formel,

A = P (1 + R/100) ⁿ

A = 10 000 (1 + 3/100) ⁴

A = 10 000 (103/100) ⁴

A = 11255

Sammansatt ränta = A – P = 11255 – 10000 = 1255

Exempel 6: Hitta den sammansatta räntan med en ränta på 5 % per år i 2 år på den kapitalbeloppet som om 2 år till en ränta på 5 % per år ges Rs. 400 som enkel ränta.

Lösning:

Given,

• Enkel ränta OM = 400
• Betyg R = 5 %
• Tid T = 2 år

Med formel,

Enkel ränta = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 Räntesats = 5 %

P = 40 000/10 = 4 000 Rs

Tid = 2 år

Med formel,

A = P (1 + R/100)

A = 4000 (1 + 5/100)

A = 4410

Sammansatt ränta = A – P = 4410 – 4000 = 410

Exempel 7: Hitta den sammansatta räntan på Rs 30000 till 7% ränta sammansatt årligen i två år.

Lösning:

• Huvudp = 30 000 Rs
• Betyg R = 7 %
• Tid = 2 år

Med formeln,

A = P (1 + R/100) ⁿ

A = 30 000 (1 + 7/100) ²

A = 30 000 (107/100) ²

A = 34347

Sammansatt ränta = A – P = 34347 – 30000 = 4347

Relaterad läsning:

• Daglig ränta
• Månatlig ränta
• Klass 8 Lösning med sammansatt ränta
• Sammansatt ränta – Lämplighetsfrågor och svar
• Enkelt intresse

Sammansatt ränta – övningsfrågor

Olika praxisfrågor om sammansatta räntor är,

Q1. Hitta det belopp som måste betalas efter 3 år om ett belopp på 10 000 lånas ut till en ränta på 4 %, sammansatt årligen.

Q2. Hitta räntan som måste betalas efter 1,5 år om en summa på 2500 lånas ut till en ränta på 6% hopsatt halvår.

Q3. Beräkna den sammansatta räntan för ett belopp på 9000 utlånat till en ränta på 5% kvartalsvis i 15 månader.

Q4. Beräkna den sammansatta räntan för ett belopp på 20 000 utlånat till en ränta på 12 % för 3 månader sammansatt månadsvis

Slutsats av ränta

Sammansatt ränta är en kraftfullt finansiellt koncept som låter investeringar eller lån växa eller ackumuleras över tid. Till skillnad från enkel ränta, som endast beräknar ränta på det ursprungliga kapitalbeloppet, ränta på ränta tar hänsyn till den intjänade räntan på både den initiala kapitalbeloppet och eventuell ackumulerad ränta från tidigare perioder.

Sammansatt ränta – Vanliga frågor

Vad betyder sammansatt ränta?

Sammansatt ränta är den ränta som beräknas på kapitalbeloppet samt den tidigare intjänade räntan under en bestämd tidsperiod

Hur beräknar man sammansatt ränta?

För att beräkna den sammansatta räntan beräknas det första slutliga beloppet och sedan dras det av från kapitalbeloppet för att få den slutliga sammansatta räntan. Beloppet beräknas med formeln,

A = P(1 + R/100) ^t

CI = A – P

Är sammansatt ränta bättre än enkelt ränta för investerare?

Ja, sammansatt ränta är mycket bättre än enkelt intresse för investerare.

Vad är Compound Interest Formula om den blandas dagligen?

Antag att den givna kapitalbeloppet är P, kursen är R, och tidsintervallet är T år, då är formeln för sammansatt ränta när den sammansätts dagligen:

A = P(1 + R/365) ^{{365 × T}}

Vad är skillnaden mellan CI och SI?

Grundskillnaden mellan CI och SI är SI är ränta som debiteras på kapitalbeloppet medan CI är ränta som debiteras på kapitalbeloppet såväl som på räntan som ackumuleras på kapitalbeloppet