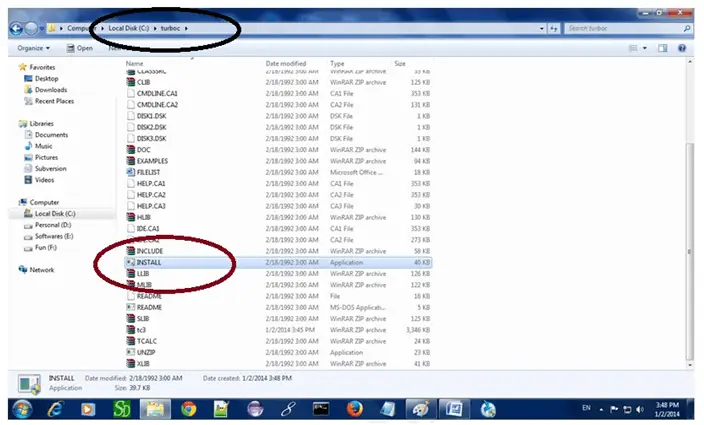
a ² – b ² formel i Algebra är den grundläggande formeln i matematik som används för att lösa olika algebraiska problem. a ² – b ² formel kallas också skillnaden mellan kvadratformel, eftersom den här formeln hjälper oss att hitta skillnaden mellan två kvadrater utan att faktiskt beräkna kvadraterna. Bilden som läggs till nedan visar formeln för a ² – b ²

I den här artikeln kommer vi att lära oss a ² – b ² formel, a ² – b ² identitet, exempel och andra i detalj.

Innehållsförteckning

• Vad är a2 – b2 formel?
• Skillnaden mellan kvadraters formel
• a2 – b2 Kvadratisk formelbevis
• (a + b)2 och (a – b)2 Formel
• a2 – b2 Identitet

Vad är a ² – b ² Formel?

a ² – b ² formel i algebra är den grundläggande formeln för att lösa algebraiska problem. Det används också för att lösa trigonometriska, differentiella och andra problem. Denna formel säger oss att skillnaden mellan kvadrat två tal är lika med produkten av summan och skillnaden mellan två tal, d.v.s.

a ² – b ² = (a + b).(a – b)

a ² – b ² Formel definition

Formeln a ² – b ² tillåter oss att bestämma variansen mellan kvadraterna av två tal utan att behöva beräkna de faktiska kvadratvärdena. Uttrycket för a ² – b ² formeln är följande: a ² – b ² = (a + b).(a – b)

Skillnaden mellan kvadraters formel

Skillnaden mellan två kvadrater beräknas med den vanliga algebraiska identiteten a ² – b ² . Till exempel får vi två variabler, a och b, sedan beräknas skillnaden mellan deras kvadrater med formeln, a ² – b ² = (a+b).(a–b)

I grund och botten säger skillnaden mellan kvadraters formel att för alla två algebraiska variabler a och b, uttrycket a ² – b ² är lika med produkten av summan och skillnaden mellan variablerna. Denna identitet används flitigt för att förenkla komplicerade algebraiska uttryck.

a ² – b ² Fyrkantigt formelbevis

a ² – b ² identitet kan bevisas genom att förenkla RHS för identiteten. Den a ² – b ² formeln ges som,

a ² – b ² = (a – b)(a + b)

Denna formel är bevisad som,

RHS = (a+b) (a–b)

⇒ RHS = a (a–b) + b (a–b)

⇒ RHS = a ² – ab + ba – b ²

⇒ RHS = a ² – ab + ab – b ²

⇒ RHS = a ² – b ²

⇒ RHS = LHS

Därav bevisat.

a ² + b ² Formel

a ² + b ² formel är den algebraiska formeln som används för att hitta summan av kvadrater av två tal. Summan av kvadratformeln ges som,

a ² + b ² = (a + b) ² – 2ab

a ² + b ² formel används för att lösa olika algebraiska problem. Olika andra viktiga algebraiska formler läggs till nedan,

(a + b) ² och (a – b) ² Formel

(a + b) ² formeln ges som,

(a + b) ² = a ² + b ² + 2ab

(a – b) ² formeln ges som,

(a – b) ² = a ² + b ² – 2ab

a ² – b ² Identitet

a ² – b ² identitet är en av de algebraiska identiteter som används för att hitta skillnaden mellan kvadrater av två tal. Denna identitet har olika tillämpningar och ges som,

a ² – b ² = (a – b).(a + b)

Läs mer,

• Algebra formel
• Grundläggande matematikformel
• Algebriskt uttryck

Exempel på a ² – b ² Formel

Exempel 1: Förenkla x ² – 16

Lösning:

= x ² – 16

= x ² - 4 ²

Vi vet det, a ² – b ² = (a+b) (a–b)

Given,

• a = x
• b = 4

= (x + 4)(x – 4)

Exempel 2: Förenkla 9y ² – 144

Lösning:

= 9 år ² – 144

= (3 år) ² – (12) ²

Vi vet det, a ² – b ² = (a+b)(a–b)

Given,

• a = 3y
• b = 12

= (3y + 12)(3y – 12)

Exempel 3: Förenkla (3x + 2) ² – (3x – 2) ²

Lösning:

Vi vet det,

a ² – b ² = (a+b)(a–b)

Given,

• a = 3x + 2
• b = 3x – 2

(3x + 2) ² – (3x – 2) ²

= (3x + 2 + 3x – 2)(3x + 2 – (3x – 2))

= 6x(3x + 2 – 3x + 2)

= 6x(4)

= 24x

Exempel 4: Förenkla och ² – 100

Lösning:

= och ² – 100

= och ² – (10) ²

Vi vet det,

a ² – b ² = (a+b)(a–b)

Given,

• a = y
• b = 10

= (y + 10)(y – 10)

Exempel 5: Utvärdera (x + 6) (x – 6)

Lösning:

Vi vet det,

(a+b) (a–b) = a ² – b ²

Given,

• a = x
• b = 6

(x + 6) (x – 6)

= x ² – 6 ²

= x ² – 36

Exempel 6: Utvärdera (y + 13)(y – 13)

Lösning:

Vi vet det,

(a+b) (a–b) = a ² – b ²

Given,

• a = y
• b = 13

(y + 13).(y – 13)

= och ² – (13) ²

= och ² – 169

Exempel 7: Utvärdera (x + y + z).(x + y – z)

Lösning:

Vi vet det,

(a+b) (a–b) = a ² – b ²

Given,

• a = x + y
• b = z

(x + y + z) (x + y – z)

= (x + y) ² - Med ²

= x ² + och ² + 2xy – z ²

(a ² – b ² ) Formel – Arbetsblad

Q1. Förenkla 15 ² – 14 ² använder en ² – b ² identitet.

Q2. Förenkla 11 ² – 7 ² använder en ² – b ² identitet.

Q3. Lös 23 ² – 9 ² använder en ² – b ² identitet.

Q4. Lös 9 ² – 7 ² använder en ² – b ² identitet.

a ² – b ² Formel – Vanliga frågor

1. Vad är en ² − b ² ?

a ² – b ² formel är formeln som används för att hitta skillnaden mellan två rutor utan att faktiskt hitta kvadraten. Den a ² – b ² formeln är,

a ² – b ² = (a + b)(a – b)

2. Vad är lagen om a ² b ² Formel?

Lagen om a ² b ² formler är,

• a ² – b ² = (a + b)(a – b)
• a ² + b ² = (a + b) ² – 2ab

3. Vad är en ² b ² Formel används för?

a ² b ² formel används för att lösa olika algebraiska problem, de används också för att förenkla trigonometriska, kalkyl- och integrationsproblem.

4. Vad är en ² b ² Formel?

Det finns två a ² b ² formler som är, a ² + b ² , och en ² – b ² expansionsformeln för a ² b ² formler ges som,

• a ² – b ² = (a + b)(a – b)
• a ² + b ² = (a + b) ² – 2ab

5. När är en ² – b ² Används formeln?

a ² – b ² formeln används för att hitta skillnaden mellan kvadrater av två tal utan att faktiskt hitta kvadraterna. Denna formel används också för att lösa olika algebraiska, trigonometriska och andra problem.