К'тх Боом Нумбер

 #працтицеЛинкДив { дисплаи: ноне !импортант; }
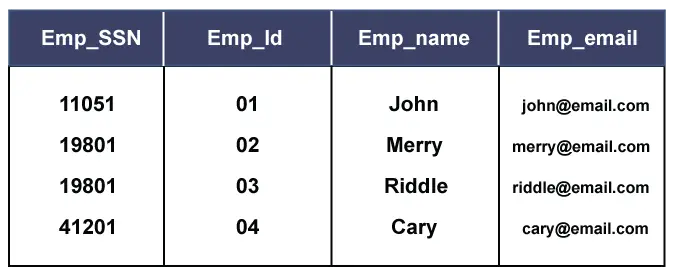
#працтицеЛинкДив { дисплаи: ноне !импортант; } Боом бројеви су бројеви који се састоје само од цифара 2 и 3. Дат цео број к (0
Input : k = 2 Output: 3 Input : k = 3 Output: 22 Input : k = 100 Output: 322323 Input: k = 1000000 Output: 3332322223223222223Recommended Practice К-ти број стреле Покушајте!
Идеја је врло једноставна као Генерисање бинарних бројева . И овде користимо исти приступ
користимо структуру података редова да решимо овај проблем. Први ред '2' па '3', ова два су први и други број гране респективно. Сада поставите цоунт=2 за сваки пут поп() испред реда и додајте '2' у искачући број и повећајте цоунт++ иф (цоунт==к), а затим одштампајте тренутни Број стреле иначе додајте '3' у искачући број и повећајте цоунт++ иф (цоунт==к), а затим одштампајте тренутни Број стреле . Понављајте процес док не стигнемо до К'тха Број стреле .
Овај приступ се може посматрати као БФС дрвета са кореном као празним низом. Лево дете сваког чвора има 2 додато, а десно дете има 3 додато.
Испод је имплементација ове идеје.
C++ // C++ program to find K'th Boom number #include using namespace std ; typedef long long int ll ; // This function uses queue data structure to K'th // Boom number void boomNumber ( ll k ) { // Create an empty queue of strings queue < string > q ; // Enqueue an empty string q . push ( '' ); // counter for K'th element ll count = 0 ; // This loop checks the value of count to // become equal to K when value of count // will be equals to k we will print the // Boom number while ( count <= k ) { // current Boom number string s1 = q . front (); // pop front q . pop (); // Store current Boom number before changing it string s2 = s1 ; // Append '2' to string s1 and enqueue it q . push ( s1 . append ( '2' )); count ++ ; // check if count==k if ( count == k ) { cout < < s1 < < endl ; // K'th Boom number break ; } // Append '3' to string s2 and enqueue it. // Note that s2 contains the previous front q . push ( s2 . append ( '3' )); count ++ ; // check if count==k if ( count == k ) { cout < < s2 < < endl ; // K'th Boom number break ; } } return ; } // Driver program to test above function int main () { ll k = 1000000 ; boomNumber ( k ); return 0 ; }
Java /*package whatever //do not write package name here */ import java.io.* ; import java.util.* ; class GFG { // This function uses queue data structure to K'th // Boom number static void boomNumber ( long k ) { // Create an empty queue of strings Queue < String > q = new LinkedList < String > (); // Enqueue an empty string q . add ( '' ); // counter for K'th element long count = 0 ; // This loop checks the value of count to // become equal to K when value of count // will be equals to k we will print the // Boom number while ( count <= k ) { // current Boom number String s1 = q . poll (); // Store current Boom number before changing it String s2 = s1 ; // Append '2' to string s1 and enqueue it q . add ( s1 + '2' ); count ++ ; // check if count==k if ( count == k ) { System . out . println ( s1 ); // K'th Boom number break ; } // Append '3' to string s2 and enqueue it. // Note that s2 contains the previous front q . add ( s2 + '3' ); count ++ ; // check if count==k if ( count == k ) { System . out . println ( s2 ); // K'th Boom number break ; } } return ; } // Driver code public static void main ( String args [] ) { long k = 1000000 ; boomNumber ( k ); } } // This code is contributed by shinjanpatra
Python3 # Python3 program to find K'th Boom number # This function uses queue data structure to K'th # Boom number def boomNumber ( k ): # Create an empty queue of strings q = [] # Enqueue an empty string q . append ( '' ) # counter for K'th element count = 0 # This loop checks the value of count to # become equal to K when value of count # will be equals to k we will print the # Boom number while ( count <= k ): # current Boom number s1 = q [ 0 ] # pop front q = q [ 1 :] # Store current Boom number before changing it s2 = s1 # Append '2' to string s1 and enqueue it s1 += '2' q . append ( s1 ) count = count + 1 # check if count==k if ( count == k ): print ( s1 ) # K'th Boom number break # Append '3' to string s2 and enqueue it. # Note that s2 contains the previous front s2 += '3' q . append ( s2 ) count = count + 1 # check if count==k if ( count == k ): print ( s2 ) # K'th Boom number break return # Driver program to test above function k = 1000000 boomNumber ( k ) # This code is contributed by shinjanpatra
C# // C# program to find K'th Boom number using System ; using System.Collections ; class GFG { // This function uses queue data structure // to K'th Boom number static void boomNumber ( long k ) { // Create an empty queue of strings Queue q = new Queue (); // Enqueue an empty string q . Enqueue ( '' ); // counter for K'th element long count = 0 ; // This loop checks the value of count to // become equal to K when value of count // will be equals to k we will print the // Boom number while ( count <= k ) { // current Boom number string s1 = ( string ) q . Dequeue (); // Store current Boom number // before changing it string s2 = s1 ; // Append '2' to string s1 and // enqueue it s1 += '2' ; q . Enqueue ( s1 ); count ++ ; // Check if count==k if ( count == k ) { // K'th Boom number Console . Write ( s1 ); break ; } // Append '3' to string s2 and enqueue it. // Note that s2 contains the previous front s2 += '3' ; q . Enqueue ( s2 ); count ++ ; // Check if count==k if ( count == k ) { // K'th Boom number Console . Write ( s2 ); break ; } } return ; } // Driver code public static void Main ( string [] arg ) { long k = 1000000 ; boomNumber ( k ); } } // This code is contributed by rutvik_56
JavaScript < script > // JavaScript program to find K'th Boom number // This function uses queue data structure to K'th // Boom number function boomNumber ( k ){ // Create an empty queue of strings let q = [] // Enqueue an empty string q . push ( '' ) // counter for K'th element let count = 0 // This loop checks the value of count to // become equal to K when value of count // will be equals to k we will print the // Boom number while ( count <= k ){ // current Boom number let s1 = q . shift () // Store current Boom number before changing it let s2 = s1 // Append '2' to string s1 and enqueue it s1 += '2' q . push ( s1 ) count = count + 1 // check if count==k if ( count == k ){ document . write ( s1 ' ' ) // K'th Boom number break } // Append '3' to string s2 and enqueue it. // Note that s2 contains the previous front s2 += '3' q . push ( s2 ) count = count + 1 // check if count==k if ( count == k ){ document . write ( s2 ' ' ) // K'th Boom number break } } return } // Driver program to test above function let k = 1000000 boomNumber ( k ) // This code is contributed by shinjanpatra < /script>
Излаз
3332322223223222223
Временска сложеност: О(К)
Помоћни простор: О(н)
Овај чланак је прегледао тим ГеексфорГеекс.