Пронађите висину посебног бинарног стабла чији су листови чворови повезани

С обзиром на а посебно бинарно дрво чији чворови листа повезани су у форму а кружна двоповезана листа задатак је пронаћи висина од дрвета.
Примери:
Улаз:

Излаз: 2
Објашњење: Висина бинарног стабла након препознавања лисних чворова је 2. У горњем бинарном стаблу 6 5 и 4 су лисни чворови и формирају кружну двоповезану листу. Овде ће леви показивач листног чвора деловати као претходни показивач кружне двоструко повезане листе, а његов десни показивач ће деловати као следећи показивач кружне двоструко повезане листе.Улаз:
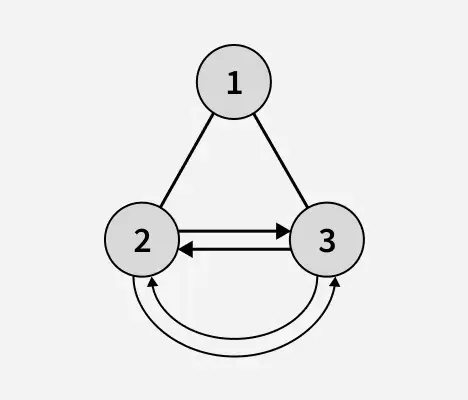
Излаз: 1
Објашњење: Висина бинарног стабла након препознавања лисних чворова је 1. У горњем бинарном стаблу 2 и 3 су лисни чворови и формирају кружну, двоструко повезану листу.
Приступ :
C++Идеја је да следи сличан приступ као што радимо за проналажење висине нормалног бинарног стабла . Ми рекурзивно израчунати висина оф лево и десно подстабла чвора и доделити висина до чвора као мак висине двоје деце плус 1. Али лево и десно дете а лисни чвор су нулл за нормална бинарна стабла. Али овде је листни чвор кружни, двоструко повезани чвор листе. Дакле, да би чвор био листни чвор, проверавамо да ли чвор лево је десно указује на чвор и њен десно је лево такође указује на чвор сама себе.
// C++ program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list #include using namespace std ; class Node { public : int data ; Node * left * right ; Node ( int x ) { data = x ; left = nullptr ; right = nullptr ; } }; // function to check if given // node is a leaf node or node bool isLeaf ( Node * node ) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other consition is also true. return node -> left && node -> left -> right == node && node -> right && node -> right -> left == node ; } // Compute the height of a tree int findTreeHeight ( Node * node ) { // if node is NULL return -1. if ( node == nullptr ) return -1 ; // if node is a leaf node return 0 if ( isLeaf ( node )) return 0 ; // compute the depth of each subtree // and take maximum return 1 + max ( findTreeHeight ( node -> left ) findTreeHeight ( node -> right )); } int main () { Node * root = new Node ( 1 ); root -> left = new Node ( 2 ); root -> right = new Node ( 3 ); root -> left -> left = new Node ( 4 ); root -> left -> right = new Node ( 5 ); root -> left -> left -> left = new Node ( 6 ); // Given tree contains 3 leaf nodes Node * l1 = root -> left -> left -> left ; Node * l2 = root -> left -> right ; Node * l3 = root -> right ; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1 -> right = l2 l2 -> right = l3 l3 -> right = l1 ; // set prev pointer of linked list l3 -> left = l2 l2 -> left = l1 l1 -> left = l3 ; cout < < findTreeHeight ( root ); return 0 ; }
C // C program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list #include #include struct Node { int data ; struct Node * left * right ; }; // function to check if given // node is a leaf node or node int isLeaf ( struct Node * node ) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other condition is also true. return node -> left && node -> left -> right == node && node -> right && node -> right -> left == node ; } // Compute the height of a tree int findTreeHeight ( struct Node * node ) { // if node is NULL return -1. if ( node == NULL ) return -1 ; // if node is a leaf node return 0 if ( isLeaf ( node )) return 0 ; // compute the depth of each subtree and take maximum int leftDepth = findTreeHeight ( node -> left ); int rightDepth = findTreeHeight ( node -> right ); return 1 + ( leftDepth > rightDepth ? leftDepth : rightDepth ); } struct Node * createNode ( int data ) { struct Node * newNode = ( struct Node * ) malloc ( sizeof ( struct Node )); newNode -> data = data ; newNode -> left = NULL ; newNode -> right = NULL ; return newNode ; } int main () { struct Node * root = createNode ( 1 ); root -> left = createNode ( 2 ); root -> right = createNode ( 3 ); root -> left -> left = createNode ( 4 ); root -> left -> right = createNode ( 5 ); root -> left -> left -> left = createNode ( 6 ); // Given tree contains 3 leaf nodes struct Node * l1 = root -> left -> left -> left ; struct Node * l2 = root -> left -> right ; struct Node * l3 = root -> right ; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1 -> right = l2 l2 -> right = l3 l3 -> right = l1 ; // set prev pointer of linked list l3 -> left = l2 l2 -> left = l1 l1 -> left = l3 ; printf ( '%d' findTreeHeight ( root )); return 0 ; }
Java // Java program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list class Node { int data ; Node left right ; Node ( int x ) { data = x ; left = null ; right = null ; } } class GfG { // function to check if given // node is a leaf node or node static boolean isLeaf ( Node node ) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other condition is also true. return node . left != null && node . left . right == node && node . right != null && node . right . left == node ; } // Compute the height of a tree static int findTreeHeight ( Node node ) { // if node is NULL return -1. if ( node == null ) return - 1 ; // if node is a leaf node return 0 if ( isLeaf ( node )) return 0 ; // compute the depth of each subtree and take maximum return 1 + Math . max ( findTreeHeight ( node . left ) findTreeHeight ( node . right )); } public static void main ( String [] args ) { Node root = new Node ( 1 ); root . left = new Node ( 2 ); root . right = new Node ( 3 ); root . left . left = new Node ( 4 ); root . left . right = new Node ( 5 ); root . left . left . left = new Node ( 6 ); // Given tree contains 3 leaf nodes Node l1 = root . left . left . left ; Node l2 = root . left . right ; Node l3 = root . right ; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1 . right = l2 ; l2 . right = l3 ; l3 . right = l1 ; // set prev pointer of linked list l3 . left = l2 ; l2 . left = l1 ; l1 . left = l3 ; System . out . println ( findTreeHeight ( root )); } }
Python # Python program to calculate height of a special tree # whose leaf nodes forms a circular doubly linked list class Node : def __init__ ( self data ): self . data = data self . left = None self . right = None # function to check if given # node is a leaf node or node def isLeaf ( node ): # For a node to be a leaf node it should # satisfy the following two conditions: # 1. Node's left's right pointer should be # current node. # 2. Node's right's left pointer should be # current node. # If one condition is met it is guaranteed # that the other condition is also true. return ( node . left and node . left . right == node and node . right and node . right . left == node ) # Compute the height of a tree def findTreeHeight ( node ): # if node is NULL return -1. if node is None : return - 1 # if node is a leaf node return 0 if isLeaf ( node ): return 0 # compute the depth of each subtree and take maximum return 1 + max ( findTreeHeight ( node . left ) findTreeHeight ( node . right )) if __name__ == '__main__' : root = Node ( 1 ) root . left = Node ( 2 ) root . right = Node ( 3 ) root . left . left = Node ( 4 ) root . left . right = Node ( 5 ) root . left . left . left = Node ( 6 ) # Given tree contains 3 leaf nodes l1 = root . left . left . left l2 = root . left . right l3 = root . right # create circular doubly linked list out of # leaf nodes of the tree # set next pointer of linked list l1 . right = l2 l2 . right = l3 l3 . right = l1 # set prev pointer of linked list l3 . left = l2 l2 . left = l1 l1 . left = l3 print ( findTreeHeight ( root ))
C# // C# program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list using System ; class Node { public int data ; public Node left right ; public Node ( int x ) { data = x ; left = null ; right = null ; } } class GfG { // function to check if given // node is a leaf node or node static bool isLeaf ( Node node ) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other condition is also true. return node . left != null && node . left . right == node && node . right != null && node . right . left == node ; } // Compute the height of a tree static int findTreeHeight ( Node node ) { // if node is NULL return -1. if ( node == null ) return - 1 ; // if node is a leaf node return 0 if ( isLeaf ( node )) return 0 ; // compute the depth of each subtree and take maximum return 1 + Math . Max ( findTreeHeight ( node . left ) findTreeHeight ( node . right )); } static void Main ( string [] args ) { Node root = new Node ( 1 ); root . left = new Node ( 2 ); root . right = new Node ( 3 ); root . left . left = new Node ( 4 ); root . left . right = new Node ( 5 ); root . left . left . left = new Node ( 6 ); // Given tree contains 3 leaf nodes Node l1 = root . left . left . left ; Node l2 = root . left . right ; Node l3 = root . right ; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1 . right = l2 ; l2 . right = l3 ; l3 . right = l1 ; // set prev pointer of linked list l3 . left = l2 ; l2 . left = l1 ; l1 . left = l3 ; Console . WriteLine ( findTreeHeight ( root )); } }
JavaScript // JavaScript program to calculate height of a special tree // whose leaf nodes forms a circular doubly linked list class Node { constructor ( data ) { this . data = data ; this . left = null ; this . right = null ; } } // function to check if given // node is a leaf node or node function isLeaf ( node ) { // For a node to be a leaf node it should // satisfy the following two conditions: // 1. Node's left's right pointer should be // current node. // 2. Node's right's left pointer should be // current node. // If one condition is met it is guaranteed // that the other condition is also true. return node . left && node . left . right === node && node . right && node . right . left === node ; } // Compute the height of a tree function findTreeHeight ( node ) { // if node is NULL return -1. if ( node === null ) return - 1 ; // if node is a leaf node return 0 if ( isLeaf ( node )) return 0 ; // compute the depth of each subtree and take maximum return 1 + Math . max ( findTreeHeight ( node . left ) findTreeHeight ( node . right )); } const root = new Node ( 1 ); root . left = new Node ( 2 ); root . right = new Node ( 3 ); root . left . left = new Node ( 4 ); root . left . right = new Node ( 5 ); root . left . left . left = new Node ( 6 ); // Given tree contains 3 leaf nodes const l1 = root . left . left . left ; const l2 = root . left . right ; const l3 = root . right ; // create circular doubly linked list out of // leaf nodes of the tree // set next pointer of linked list l1 . right = l2 ; l2 . right = l3 ; l3 . right = l1 ; // set prev pointer of linked list l3 . left = l2 ; l2 . left = l1 ; l1 . left = l3 ; console . log ( findTreeHeight ( root ));
Излаз
3
Временска сложеност: О(н) где н је број чворова.
Помоћни простор: О(х)