Биномне случајне варијабле

У овом посту ћемо разговарати о биномним случајним променљивим.
Предуслов: Рандом Вариаблес
Специфична врста дискретно случајна променљива која броји колико често се одређени догађај дешава у фиксном броју покушаја или покушаја.
Да би променљива била биномна случајна променљива, морају бити испуњени СВИ следећи услови:
- Постоји фиксни број испитивања (фиксна величина узорка).
- У сваком испитивању се догађај од интереса или догоди или не.
- Вероватноћа појаве (или не) је иста у сваком испитивању.
- Суђења су независна једно од другог.
Матхематицал Нотатионс
n = number of trials
p = probability of success in each trial
k = number of success in n trials
Сада покушавамо да сазнамо вероватноћу к успеха у н покушаја.
Овде је вероватноћа успеха у сваком огледу п независно од других покушаја.
Дакле, прво бирамо к покушаја у којима ће бити успеха, ау осталим н-к покушаја ће бити неуспеха. Број начина да се то уради је

Пошто је свих н догађаја независно, вероватноћа к успеха у н покушаја је еквивалентна множењу вероватноће за сваки покушај.
Овде је к успеха и н-к неуспеха, па је вероватноћа за сваки начин да се постигне к успеха и н-к неуспеха је

Дакле, коначна вероватноћа је
(number of ways to achieve k success
and n-k failures)
*
(probability for each way to achieve k
success and n-k failure)
Тада је вероватноћа биномне случајне променљиве дата са:

Нека је Кс биномна случајна променљива са бројем покушаја н и вероватноћом успеха у сваком покушају је п.
Очекивани број успеха је дат по
E[X] = np
Варијанца броја успеха је дата са
Var[X] = np(1-p)
Пример 1 : Размислите о насумичном експерименту у којем је пристрасни новчић (вероватноћа главе = 1/3) бачен 10 пута. Нађите вероватноћу да ће број глава које ће се појавити бити 5.
решење:
Let X be binomial random variable
with n = 10 and p = 1/3
P(X=5) = ?

Ево имплементације за исто
C++
Java// C++ program to compute Binomial Probability #include#include using namespace std ; // function to calculate nCr i.e. number of // ways to choose r out of n objects int nCr ( int n int r ) { // Since nCr is same as nC(n-r) // To decrease number of iterations if ( r > n / 2 ) r = n - r ; int answer = 1 ; for ( int i = 1 ; i <= r ; i ++ ) { answer *= ( n - r + i ); answer /= i ; } return answer ; } // function to calculate binomial r.v. probability float binomialProbability ( int n int k float p ) { return nCr ( n k ) * pow ( p k ) * pow ( 1 - p n - k ); } // Driver code int main () { int n = 10 ; int k = 5 ; float p = 1.0 / 3 ; float probability = binomialProbability ( n k p ); cout < < 'Probability of ' < < k ; cout < < ' heads when a coin is tossed ' < < n ; cout < < ' times where probability of each head is ' < < p < < endl ; cout < < ' is = ' < < probability < < endl ; } Python3// Java program to compute Binomial Probability import java.util.* ; class GFG { // function to calculate nCr i.e. number of // ways to choose r out of n objects static int nCr ( int n int r ) { // Since nCr is same as nC(n-r) // To decrease number of iterations if ( r > n / 2 ) r = n - r ; int answer = 1 ; for ( int i = 1 ; i <= r ; i ++ ) { answer *= ( n - r + i ); answer /= i ; } return answer ; } // function to calculate binomial r.v. probability static float binomialProbability ( int n int k float p ) { return nCr ( n k ) * ( float ) Math . pow ( p k ) * ( float ) Math . pow ( 1 - p n - k ); } // Driver code public static void main ( String [] args ) { int n = 10 ; int k = 5 ; float p = ( float ) 1.0 / 3 ; float probability = binomialProbability ( n k p ); System . out . print ( 'Probability of ' + k ); System . out . print ( ' heads when a coin is tossed ' + n ); System . out . println ( ' times where probability of each head is ' + p ); System . out . println ( ' is = ' + probability ); } } /* This code is contributed by Mr. Somesh Awasthi */C## Python3 program to compute Binomial # Probability # function to calculate nCr i.e. # number of ways to choose r out # of n objects def nCr ( n r ): # Since nCr is same as nC(n-r) # To decrease number of iterations if ( r > n / 2 ): r = n - r ; answer = 1 ; for i in range ( 1 r + 1 ): answer *= ( n - r + i ); answer /= i ; return answer ; # function to calculate binomial r.v. # probability def binomialProbability ( n k p ): return ( nCr ( n k ) * pow ( p k ) * pow ( 1 - p n - k )); # Driver code n = 10 ; k = 5 ; p = 1.0 / 3 ; probability = binomialProbability ( n k p ); print ( 'Probability of' k 'heads when a coin is tossed' end = ' ' ); print ( n 'times where probability of each head is' round ( p 6 )); print ( 'is = ' round ( probability 6 )); # This code is contributed by mitsJavaScript// C# program to compute Binomial // Probability. using System ; class GFG { // function to calculate nCr // i.e. number of ways to // choose r out of n objects static int nCr ( int n int r ) { // Since nCr is same as // nC(n-r) To decrease // number of iterations if ( r > n / 2 ) r = n - r ; int answer = 1 ; for ( int i = 1 ; i <= r ; i ++ ) { answer *= ( n - r + i ); answer /= i ; } return answer ; } // function to calculate binomial // r.v. probability static float binomialProbability ( int n int k float p ) { return nCr ( n k ) * ( float ) Math . Pow ( p k ) * ( float ) Math . Pow ( 1 - p n - k ); } // Driver code public static void Main () { int n = 10 ; int k = 5 ; float p = ( float ) 1.0 / 3 ; float probability = binomialProbability ( n k p ); Console . Write ( 'Probability of ' + k ); Console . Write ( ' heads when a coin ' + 'is tossed ' + n ); Console . Write ( ' times where ' + 'probability of each head is ' + p ); Console . Write ( ' is = ' + probability ); } } // This code is contributed by nitin mittal.PHP< script > // Javascript program to compute Binomial Probability // function to calculate nCr i.e. number of // ways to choose r out of n objects function nCr ( n r ) { // Since nCr is same as nC(n-r) // To decrease number of iterations if ( r > n / 2 ) r = n - r ; let answer = 1 ; for ( let i = 1 ; i <= r ; i ++ ) { answer *= ( n - r + i ); answer /= i ; } return answer ; } // function to calculate binomial r.v. probability function binomialProbability ( n k p ) { return nCr ( n k ) * Math . pow ( p k ) * Math . pow ( 1 - p n - k ); } // driver program let n = 10 ; let k = 5 ; let p = 1.0 / 3 ; let probability = binomialProbability ( n k p ); document . write ( 'Probability of ' + k ); document . write ( ' heads when a coin is tossed ' + n ); document . write ( ' times where probability of each head is ' + p ); document . write ( ' is = ' + probability ); // This code is contributed by code_hunt. < /script>Излаз:
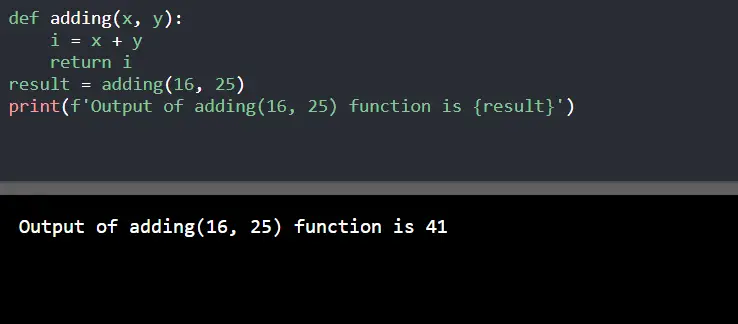
Probability of 5 heads when a coin is tossed 10 times where probability of each head is 0.333333
is = 0.136565Креирај квиз