Pravila sklepanja: Vsak matematični izrek ali kateri koli predmet je podprt z osnovnimi dokazi . Ti dokazi niso nič drugega kot niz argumentov, ki so prepričljivi dokazi o veljavnosti teorije. Argumenti so verižno povezani z uporabo pravil sklepanja, da se izpeljejo nove izjave in na koncu dokaže, da je izrek veljaven.

Kazalo

• Definicije
• Tabela pravil sklepanja
• Pravila sklepanja
• Načelo ločljivosti:
• Primer pravila sklepanja,

Definicije

• Prepir - Zaporedje izjav in prostorov , ki se končajo z zaključkom.
• Veljavnost – Za deduktivni argument velja, če in samo če ima obliko, ki onemogoča, da bi bile premise resnične, sklep pa kljub temu napačen.
• Zmota – Nepravilno razmišljanje ali napaka, ki vodi do neveljavnih argumentov.

Tabela pravil sklepanja

Struktura argumenta: Kot je definirano, je argument zaporedje izjav, imenovanih premise, ki se končajo z zaključkom.

Prostori - p_{1},:p_{2},:p_{3},..., :p_{n}
Zaključek - q

if(p_{1}wedge p_{2}wedge p_{3}wedge … wedge p_{n}) ightarrow q je tavtologija, potem je argument označen kot veljaven, drugače označen kot neveljaven. Argument je zapisan kot –

First PremiseSecond PremiseThird Premise...Nth Premise\therefore Conclusion

Pravila sklepanja

Enostavne argumente je mogoče uporabiti kot gradnike za sestavo bolj zapletenih veljavnih argumentov. Nekateri preprosti argumenti, ki so bili uveljavljeni kot veljavni, so zelo pomembni z vidika njihove uporabe. Ti argumenti se imenujejo pravila sklepanja. Najpogosteje uporabljena pravila sklepanja so navedena spodaj –

Podobno imamo pravila sklepanja za kvantificirane izjave –

Poglejmo, kako je mogoče uporabiti pravila sklepanja za sklepanje sklepov iz danih argumentov ali preverjanje veljavnosti danega argumenta.

Primer: Pokažite, da hipoteze Danes popoldne ni sonca in je hladneje kot včeraj , Kopat se bomo šli le, če bo sončno , Če ne gremo kopat, se bomo odpravili na izlet s kanujem , in Če gremo na izlet s kanujem, potem do sončnega zahoda bomo doma vodi do zaključka Do sončnega zahoda bomo doma .

Prvi korak je identificirati predloge in uporabiti propozicionalne spremenljivke za njihovo predstavitev.

p- Danes popoldne je sončno q- Je hladneje kot včeraj r- Šli bomo plavat s- Odpeljali se bomo na izlet s kanujem t- Do sončnega zahoda bomo doma

Hipoteze so – eg p wedge q , r ightarrow p , eg r ightarrow s , in s ightarrow t . Zaključek je – t Za izpeljavo zaključka moramo uporabiti pravila sklepanja, da zgradimo dokaz z uporabo danih hipotez. egin{tabular} hline Step & Reason hline hline 1. eg p wedge q & Hypothesis 2. eg p & Simplification 3. r ightarrow p & Hypothesis 4. eg r & Modus Tollens using (2) and (3) 5. eg r ightarrow s & Hypothesis 6. s & Modus Ponens using (4) and (5) 7. s ightarrow t & Hypothesis 8. t & Modus Ponens Using (6) and (7) hline end{tabular}

Načelo ločljivosti

Da bi razumeli načelo reševanja, moramo najprej poznati določene definicije.

• dobesedno – Spremenljivka ali negacija spremenljivke. npr. p, eg q
• Vsota – Disjunkcija literalov. npr. pvee eg q
• izdelek – Konjunkcija literalov. npr. p wedge eg q
• Klavzula – Disjunkcija literalov, tj. je vsota.
• Resolvent – Za katera koli dva stavka C_{1} in C_{2} , če obstaja dobesedno L_{1} v C_{1} ki dopolnjuje dobesedno L_{2} v C_{2} , nato odstranitev obeh in združevanje preostalih klavzul z disjunkcijo proizvede še eno klavzulo C . C imenujemo razrešnica C_{1} in C_{2}

Primer pravila sklepanja

C_{1} = pvee qvee r C_{2} = eg pvee eg s vee t

tukaj, eg p in p se med seboj dopolnjujejo. Če jih odstranimo in združimo preostale člene z disjunkcijo, dobimo- qvee r vee eg svee t Lahko bi preskočili del odstranitve in preprosto združili klavzule, da bi dobili enako rešitev t. since p vee eg p equiv T: and,: T vee q equiv q

To je tudi pravilo sklepanja, znano kot razrešitev. izrek – če C je razrešilec C_{1} in C_{2} , potem C je tudi logična posledica od C_{1} in C_{2} . Načelo ločljivosti – Podan komplet S of clauses, a (resolution) deduction of C od S je končno zaporedje C_{1}, C_{2},…, C_{k} klavzul, tako da vsak C_{i} je bodisi klavzula v S ali ločilo predhodnih členov C in C_{k} = C

Načelo razrešitve lahko uporabimo za preverjanje veljavnosti argumentov ali iz njih sklepamo. Druga pravila sklepanja imajo enak namen, vendar je Resolution edinstven. Popoln je sam po sebi. Za izpeljavo zaključka iz danega argumenta ne potrebujete nobenega drugega pravila sklepanja. Da bi to naredili, moramo najprej pretvoriti vse premise v klavzalno obliko. Naslednji korak je, da zanje korak za korakom uporabite pravilo sklepanja, dokler ga ne bo več mogoče uporabiti. Na primer, upoštevajte, da imamo naslednje prostore –

p ightarrow (qvee r) s ightarrow eg r pwedge s

Prvi korak je, da jih pretvorite v klavzalno obliko –

C_{1}: : eg pvee qvee r C_{2}: : eg svee eg r C_{3}: :p C_{4}: :s Iz resolucije z dne C_{1} in C_{2} , C_{5}:: eg pvee qvee eg s Iz resolucije z dne C_{5} in C_{3} , C_{6}:: qvee eg s Iz resolucije z dne C_{6} in C_{4} , C_{7}:: q Zato je sklep q .

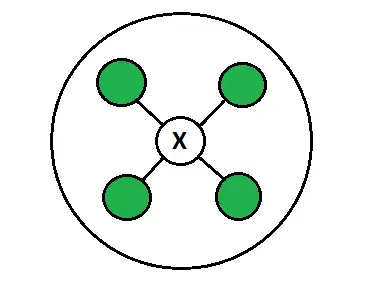
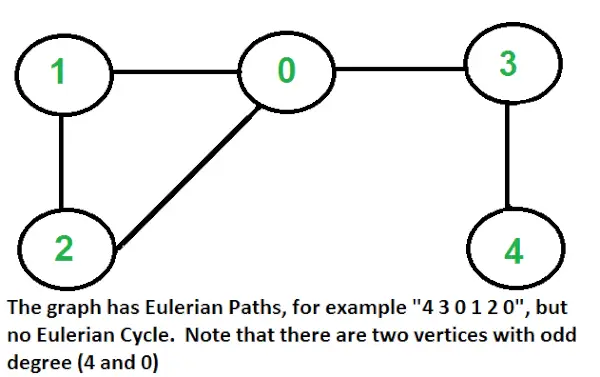
Opomba: Posledice je mogoče vizualizirati tudi na osmerokotnik kot, Prikazuje, kako se implikacija spreminja ob spreminjanju vrstnega reda njihovih obstojov in za vse simbole. GATE CS Corner Vprašanja Vadba naslednjih vprašanj vam bo pomagala preveriti svoje znanje. Vsa vprašanja so bila postavljena v GATE v prejšnjih letih ali v GATE Mock Tests.

Zelo priporočljivo je, da jih izvajate.

• GATE CS 2004, vprašanje 70
• GATE CS 2015 Set-2, vprašanje 13

Reference -

• Pravila sklepanja
• Univerza Simon Fraser Pravila sklepanja
• Wikipedia Zmota
• Wikipedia Knjiga
• Diskretna matematika in
• Njegove aplikacije Kennetha Rosena

Zaključek – Pravila sklepanja

V logiki vsako pravilo sklepanja vodi do določenega zaključka na podlagi danih premis. Modus Ponens ugotavlja, da če izjava P implicira Q in je P resničen, mora biti tudi Q resničen. Nasprotno pa Modus Tollens trdi, da če P implicira Q in je Q napačen, mora biti P napačen. Hipotetični silogizem razširja to razmišljanje z navedbo, da če P implicira Q in Q implicira R, potem P implicira R. Disjunktivni silogizem trdi, da če je P ali Q resničen in je P napačen, potem mora biti Q resničen. Seštevanje pomeni, da če je P res, potem je P ali Q res. Poenostavitev narekuje, da če sta P in Q resnična, potem mora biti P resničen. Nazadnje, Konjunkcija navaja, da če sta P in Q resnična, potem sta P in Q resnična. Ta pravila skupaj zagotavljajo okvir za logično sklepanje iz danih izjav.

Pravilo sklepanja – pogosta vprašanja

Kakšna so pravila sklepanja, pojasnite s primeri?

Pravilo sklepanja, znano kot modus ponens. Vključuje dva stavka: enega v obliki Če p, potem q in drugega, ki preprosto navaja p. Ko te premise združimo, pride do zaključka q.

Katerih je 8 veljavnih pravil sklepanja?

Zajemajo tudi osem veljavnih oblik sklepanja: modus ponens, modus tollens, hipotetični silogizem, poenostavitev, konjunkcijo, disjunktivni silogizem, seštevanje in konstruktivno dilemo.

Kaj je primer pravil razrešitve sklepanja?

Če bo snežilo, bom študiral diskretno matematiko. Če bom študiral diskretno matematiko, bom dobil petico. Torej, če bo snežilo, bom dobil petico.

Primer pravila sklepanja: modus ponens?

• Če dežuje (P), so tla mokra (Q).
• Res dežuje (P).
• Zato lahko sklepamo, da so tla mokra (Q).

Ta logični proces je znan kot modus ponens.

Katerih je 7 pravil sklepanja?

Sedem pogosto uporabljenih pravil sklepanja v logiki je:

Način nastavitve (MP)

Mode Tollens (MT)

Hipotetični silogizem (HS)

Disjunktivni silogizem (DS)

Dodatek (Dodaj)

Poenostavitev (Simp)

veznik (conj)

Če ti je všeč techcodeview.com in bi radi prispevali, lahko tudi napišete članek z uporabo Oglejte si, da se vaš članek pojavi na glavni strani techcodeview.com in pomagajte drugim Geekom. Prosimo, napišite komentarje, če najdete kar koli nepravilnega ali želite deliti več informacij o zgoraj obravnavani temi.