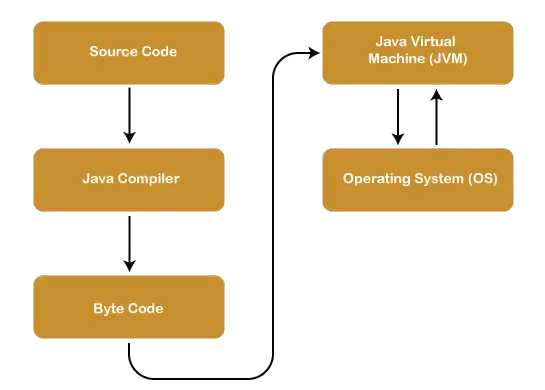
Planarni graf:

Graf je ravninski, če ga lahko narišemo v ravnini tako, da noben rob ne prečka.
primer: Graf, prikazan na sliki, je ravninski graf.


Območje grafa: Razmislite o ravninskem grafu G=(V,E). Regija je definirana kot območje ravnine, ki je omejeno z robovi in ga ni mogoče nadalje razdeliti. Planarni graf razdeli načrte na eno ali več regij. Ena od teh regij bo neskončna.
Končna regija: Če je območje območja končno, se to območje imenuje končno območje.
Neskončno območje: Če je površina regije neskončna, se ta regija imenuje neskončna regija. Planarni graf ima samo eno neskončno regijo.
primer: Razmislite o grafu, prikazanem na sliki. Določite število regij, končnih regij in neskončne regije.

rešitev: V zgornjem grafu je pet regij, tj 1 ,r 2 ,r 3 ,r 4 ,r 5 .
V grafu so štiri končne regije, tj. r 2 ,r 3 ,r 4 ,r 5 .
Obstaja samo ena končna regija, to je r 1
Lastnosti ravninskih grafov:
- Če ima povezan ravninski graf G e robov in r regij, potem je r ≦
 Je.
Je. - Če ima povezan ravninski graf G e robov, v oglišč in r regij, potem je v-e+r=2.
- Če ima povezan ravninski graf G e robov in v oglišč, potem velja 3v-e≧6.
- Celoten graf K n je ravnina, če in samo če je n <5. < li>
- Popolni bipartitni graf K mn je ravninska, če in samo, če je m3.
primer: Dokažite, da popoln graf K 4 je planaren.
rešitev: Celoten graf K 4 vsebuje 4 oglišča in 6 robov.
Vemo, da za povezan ravninski graf velja 3v-e≧6. Zato za K 4 , imamo 3x4-6=6, kar zadošča lastnosti (3).
Tako je K 4 je ravninski graf. Zato dokazano.
Neplanarni graf:
Za graf pravimo, da ni ravninski, če ga ni mogoče narisati v ravnino, tako da noben rob ne prečka.
primer: Grafi, prikazani na sliki, so neplanarni grafi.

Teh grafov ni mogoče narisati v ravnini, tako da se robovi ne sekajo, zato so neplanarni grafi.
Lastnosti neplanarnih grafov:
Graf je neplanaren, če in samo če vsebuje podgraf, homeomorfen K 5 ali K 3.3
Primer1: Pokaži, da je K 5 je neplanarna.
rešitev: Celoten graf K 5 vsebuje 5 oglišč in 10 robov.
Zdaj pa za povezani ravninski graf 3v-e≧6.
Zato je za K 5 , imamo 3 x 5-10=5 (kar ne izpolnjuje lastnosti 3, ker mora biti večje ali enako 6).
Tako je K 5 je neplanaren graf.
Primer2: Dokažite, da so grafi, prikazani na sliki, neplanarni, tako da poiščete podgraf, homeomorfen K 5 ali K 3.3 .


rešitev: Če odstranimo robove (V 1 ,IN 4 ),(IN 3 ,IN 4 ) in (V 5 ,IN 4 ) graf G 1 , postane homeomorfen s K 5 .Zato je neplanarna.
Če odstranimo rob V 2,V 7) graf G 2 postane homeomorfen K 3.3 .Zato je neravninski.
Barvanje grafa:
Recimo, da je G= (V,E) graf brez več robov. Barvanje vozlišč G je dodelitev barv vozliščem G, tako da imajo sosednja vozlišča različne barve. Graf G je M-obarvan, če obstaja barvanje G, ki uporablja M-barve.
Pravilno barvanje: Barvanje je pravilno, če imata kateri koli dve sosednji vozlišči u in v različni barvi, sicer se imenuje nepravilno barvanje.
primer: Razmislite o naslednjem grafu in pobarvajte C={r, w, b, y}. Graf pravilno pobarvajte z vsemi ali manj barvami.

Graf, prikazan na sliki, je najmanj 3-barven, zato je x(G)=3
rešitev: Slika prikazuje pravilno obarvan graf z vsemi štirimi barvami.

Slika prikazuje graf, pravilno obarvan s tremi barvami.

Kromatsko število G: Najmanjše število barv, potrebnih za pravilno barvanje grafa G, se imenuje kromatsko število G in je označeno z x(G).
primer: Kromatsko število K n je n.
rešitev: Barva K n lahko sestavite z uporabo n barv tako, da vsakemu vozlišču dodelite različne barve. Dvema vozliščema ni mogoče dodeliti enakih barv, saj sta vsaki dve točki tega grafa sosednji. Od tod kromatsko število K n =n.
Uporaba barvanja grafov
Nekatere aplikacije barvanja grafov vključujejo:
- Registracija Dodelitev
- Barvanje zemljevida
- Preverjanje bipartitnega grafa
- Dodelitev mobilne radijske frekvence
- Izdelava urnika itd.
Navedite in dokažite izrek rokovanja.
Izrek o rokovanju: Vsota stopinj vseh vozlišč v grafu G je enaka dvakratnemu številu robov v grafu.
Matematično se lahko izrazi kot:
∑ v∈V deg(v)=2e
Dokaz: Naj bo G = (V, E) graf, kjer je V = {v 1 ,v 2 , . . . . . . . . . .} je množica vozlišč in E = {e 1 ,Je 2 . . . . . . . . . .} je množica robov. Vemo, da vsak rob leži med dvema vozliščema, tako da vsakemu vozlišču zagotavlja stopnjo ena. Zato vsak rob prispeva dve stopnji za graf. Torej je vsota stopinj vseh oglišč enaka dvakratnemu številu robov v G.
Torej, ∑ v∈V deg(v)=2e