Ta vadnica je začetnikom prijazen vodnik za učenje podatkovnih struktur in algoritmov z uporabo Pythona. V tem članku bomo razpravljali o vgrajenih podatkovnih strukturah, kot so seznami, tuple, slovarji itd., in nekaterih uporabniško definiranih podatkovnih strukturah, kot je npr. povezani seznami , drevesa , grafi itd. ter algoritme prečkanja ter iskanja in razvrščanja s pomočjo dobrih in dobro razloženih primerov ter vprašanj za prakso.

Seznami

Seznami Python so urejene zbirke podatkov tako kot polja v drugih programskih jezikih. Omogoča različne vrste elementov na seznamu. Implementacija Python List je podobna Vectors v C++ ali ArrayList v JAVA. Draga operacija je vstavljanje ali brisanje elementa z začetka seznama, saj je treba vse elemente premakniti. Vstavljanje in brisanje na koncu seznama lahko postane drago tudi v primeru, ko je vnaprej dodeljeni pomnilnik poln.

Primer: Ustvarjanje seznama Python

List = [1, 2, 3, 'GFG', 2.3] print(List) 

[1, 2, 3, 'GFG', 2.3] 

Do elementov seznama lahko dostopate z dodeljenim indeksom. V pythonu je začetni indeks seznama zaporedje 0, končni indeks pa (če je N elementov) N-1.

Primer: operacije seznama Python

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3]) 

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks 

Tuple

Python tuples so podobni seznamom, Tuples pa so nespremenljiv v naravi, tj. ko je ustvarjen, ga ni več mogoče spreminjati. Tako kot seznam lahko tudi Tuple vsebuje elemente različnih vrst.

V Pythonu so tuple ustvarjene z umestitvijo zaporedja vrednosti, ločenih z 'vejico' z ali brez uporabe oklepajev za združevanje zaporedja podatkov.

Opomba: Če želite ustvariti tulp iz enega elementa, mora biti na koncu vejica. Na primer, (8,) bo ustvaril torko, ki vsebuje 8 kot element.

Primer: Python Tuple Operations

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3]) 

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 

Set

Python set je spremenljiva zbirka podatkov, ki ne dovoljuje podvajanja. Kompleti se v bistvu uporabljajo za vključitev testiranja članstva in odstranjevanje podvojenih vnosov. Pri tem uporabljena podatkovna struktura je zgoščevanje, priljubljena tehnika za izvajanje vstavljanja, brisanja in prečkanja v povprečju O(1).

Če je na istem mestu indeksa prisotnih več vrednosti, je vrednost dodana temu položaju indeksa, da se oblikuje povezan seznam. V CPython Sets so implementirani z uporabo slovarja z navideznimi spremenljivkami, kjer so ključna bitja člani niza z večjo optimizacijo časovne kompleksnosti.

Nastavite implementacijo:

Nabori s številnimi operacijami na eni HashTable:

Primer: Python Set Operations

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set) 

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True 

Zamrznjeni kompleti

Zamrznjeni kompleti v Pythonu so nespremenljivi objekti, ki podpirajo le metode in operatorje, ki ustvarijo rezultat, ne da bi vplivali na zamrznjeni niz ali nize, za katere so uporabljeni. Medtem ko je elemente niza mogoče kadar koli spremeniti, elementi zamrznjenega niza po ustvarjanju ostanejo enaki.

Primer: nabor Python Frozen

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h') 

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'}) 

Vrvica

Python nizi je nespremenljivo polje bajtov, ki predstavljajo znake Unicode. Python nima znakovnega podatkovnega tipa, en sam znak je preprosto niz z dolžino 1.

Opomba: Ker so nizi nespremenljivi, bo sprememba niza povzročila ustvarjanje nove kopije.

Primer: operacije nizov Python

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1]) 

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s 

Slovar

Slovar Python je neurejena zbirka podatkov, ki shranjuje podatke v obliki para ključ:vrednost. Je kot zgoščene tabele v katerem koli drugem jeziku s časovno kompleksnostjo O(1). Indeksiranje slovarja Python poteka s pomočjo tipk. Ti so katerega koli tipa, ki ga je mogoče razpršiti, tj. objekt, ki se nikoli ne more spremeniti, kot so nizi, števila, tuple itd. Slovar lahko ustvarimo z uporabo zavitih oklepajev ({}) ali razumevanja slovarja.

Primer: operacije slovarja Python

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict) 

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} 

Matrix

Matrika je dvodimenzionalni niz, kjer je vsak element popolnoma enake velikosti. Za izdelavo matrike bomo uporabili Paket NumPy .

Primer: matrične operacije Python NumPy

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m) 

Izhod

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] 

Bytearray

Python Bytearray daje spremenljivo zaporedje celih števil v območju 0 <= x < 256.

Primer: operacije Python Bytearray

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a) 

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e') 

Povezan seznam

A povezan seznam je linearna podatkovna struktura, v kateri elementi niso shranjeni na sosednjih pomnilniških lokacijah. Elementi na povezanem seznamu so povezani s kazalci, kot je prikazano na spodnji sliki:

Povezani seznam je predstavljen s kazalcem na prvo vozlišče povezanega seznama. Prvo vozlišče se imenuje glava. Če je povezan seznam prazen, je vrednost glave NULL. Vsako vozlišče na seznamu je sestavljeno iz vsaj dveh delov:

• podatki
• Kazalec (ali sklic) na naslednje vozlišče

Primer: Definiranje povezanega seznama v Pythonu

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None 

Ustvarimo preprost povezan seznam s 3 vozlišči.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | nič | | 3 | nič |  +----+------+ +----+------+ +----+------+ ''' drugi.naslednji = tretji ; # Povežite drugo vozlišče s tretjim vozliščem ''' Zdaj se naslednje od drugega vozlišča nanaša na tretje. Torej so vsa tri vozlišča povezana.  llist.head drugi tretji | | |  | | |  +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | nič |  +----+------+ +----+------+ +----+------+ ''' 

Prehod povezanega seznama

V prejšnjem programu smo ustvarili preprost povezan seznam s tremi vozlišči. Preletimo ustvarjeni seznam in natisnemo podatke vsakega vozlišča. Za prečkanje napišimo splošno uporabno funkcijo printList(), ki natisne poljuben seznam.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList() 

1 2 3 

Več člankov na povezanem seznamu

• Vstavljanje povezanega seznama
• Brisanje povezanega seznama (brisanje danega ključa)
• Brisanje povezanega seznama (brisanje ključa na danem mestu)
• Iskanje dolžine povezanega seznama (iterativno in rekurzivno)
• Iskanje elementa na povezanem seznamu (iterativno in rekurzivno)
• N-to vozlišče od konca povezanega seznama
• Obrnite povezani seznam

A kup je linearna podatkovna struktura, ki shranjuje elemente na način Zadnji vstop/prvi ven (LIFO) ali Prvi vstop/Zadnji ven (FILO). V skladu je nov element dodan na enem koncu in element je odstranjen samo s tega konca. Operaciji vstavljanja in brisanja se pogosto imenujeta push in pop.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty 

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: [] 

Kot kup, čakalna vrsta je linearna podatkovna struktura, ki shranjuje elemente na način First In First Out (FIFO). Pri čakalni vrsti se najprej odstrani nazadnje dodan element. Dober primer čakalne vrste je katera koli čakalna vrsta porabnikov za vir, kjer je porabnik, ki je bil prvi, postrežen prvi.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty 

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements [] 

Prednostne čakalne vrste so abstraktne podatkovne strukture, kjer ima vsak podatek/vrednost v čakalni vrsti določeno prioriteto. Na primer, pri letalskih družbah prtljaga z naslovom Business ali First-class prispe prej kot ostala. Prednostna čakalna vrsta je razširitev čakalne vrste z naslednjimi lastnostmi.

• Element z visoko prioriteto je izključen iz čakalne vrste pred elementom z nizko prioriteto.
• Če imata dva elementa enako prednost, se strežeta glede na vrstni red v čakalni vrsti.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] return item razen IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue), medtem ko ni myQueue.isEmpty(): print(myQueue.delete()) 

12 1 14 7 14 12 7 1 

Kup

modul heapq v Pythonu zagotavlja podatkovno strukturo kopice, ki se večinoma uporablja za predstavitev prednostne čakalne vrste. Lastnost te podatkovne strukture je, da vedno daje najmanjši element (najmanjšo kopico), kadar koli je element iztisnjen. Kadarkoli se elementi potisnejo ali izskočijo, se struktura kopice ohrani. Element heap[0] prav tako vsakič vrne najmanjši element. Podpira ekstrakcijo in vstavljanje najmanjšega elementa v časih O(log n).

Na splošno so kopice lahko dveh vrst:

• Največji kup: V Max-Heap mora biti ključ, ki je prisoten v korenskem vozlišču, največji med ključi, ki so prisotni pri vseh njegovih podrejenih. Ista lastnost mora biti rekurzivno resnična za vsa poddrevesa v tem binarnem drevesu.
• Najmanjša kopica: V Min-Heap mora biti ključ, prisoten v korenskem vozlišču, minimalen med ključi, ki so prisotni pri vseh njegovih podrejenih elementih. Ista lastnost mora biti rekurzivno resnična za vsa poddrevesa v tem binarnem drevesu.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li)) 

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1 

Več člankov o Heap

• Binarna kopica
• K-ti največji element v nizu
• K’th najmanjši/največji element v nerazvrščenem nizu
• Razvrsti skoraj razvrščeno matriko
• K-ti največji sosednji podniz vsote
• Najmanjša vsota dveh števil, sestavljena iz števk matrike

Drevo je hierarhična podatkovna struktura, ki izgleda kot spodnja slika –

 tree  ----  j  <-- root  /   f k  /   a h z  <-- leaves 

Najvišje vozlišče drevesa se imenuje koren, medtem ko se najnižja vozlišča ali vozlišča brez otrok imenujejo listna vozlišča. Vozlišča, ki so neposredno pod vozliščem, se imenujejo njegovi otroci, vozlišča, ki so neposredno nad nečim, pa se imenujejo njegov nadrejeni.

A binarno drevo je drevo, katerega elementi imajo lahko skoraj dva otroka. Ker ima lahko vsak element v binarnem drevesu samo 2 otroka, ju običajno imenujemo levi in ​​desni otrok. Vozlišče binarnega drevesa vsebuje naslednje dele.

• podatki
• Kazalec na levega otroka
• Kazalec na pravega otroka

Primer: Definiranje razreda vozlišča

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key 

Zdaj pa ustvarimo drevo s 4 vozlišči v Pythonu. Predpostavimo, da je drevesna struktura videti spodaj –

 tree  ----  1  <-- root  /   2 3   /  4 

Primer: dodajanje podatkov v drevo

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None''' 

Prehod drevesa

Drevesa je mogoče prečkati na različne načine. Sledijo običajno uporabljeni načini za prečenje dreves. Oglejmo si spodnje drevo –

 tree  ----  1  <-- root  /   2 3   /  4 5 

Prvi prehodi globine:

• Vrstni red (levo, koren, desno): 4 2 5 1 3
• Prednaročilo (Root, Left, Right): 1 2 4 5 3
• Po naročilu (levo, desno, koren): 4 5 2 3 1

Algoritem po vrstnem redu (drevo)

• Prečkaj levo poddrevo, tj. pokliči Inorder(left-subtree)
• Obiščite koren.
• Prečkaj desno poddrevo, tj. pokliči Inorder(right-subtree)

Prednaročilo algoritma (drevo)

• Obiščite koren.
• Prečkaj levo poddrevo, tj. pokliči Preorder(left-subtree)
• Prečkaj desno poddrevo, tj. pokliči Preorder(right-subtree)

Algoritem Poštna nakaznica (drevo)

• Prečkajte levo poddrevo, tj. pokličite Postorder(left-subtree)
• Prečkaj desno poddrevo, tj. pokliči Postorder(right-subtree)
• Obiščite koren.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root) 

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1 

Časovna kompleksnost – O(n)

Prehod vrstnega reda prve stopnje ali ravni

Prehod ravni vrstnega reda drevesa je prehod drevesa v širino. Vrstni red prečkanja zgornjega drevesa je 1 2 3 4 5.

Za vsako vozlišče se najprej obišče vozlišče, nato pa se njegova podrejena vozlišča postavijo v čakalno vrsto FIFO. Spodaj je algoritem za isto –

• Ustvarite prazno čakalno vrsto q
• temp_node = koren /*začetek od korena*/
• Zanka, medtem ko temp_node ni NULL
  • natisni temp_node->data.
  • Postavite otroke temp_node (najprej leve in nato desne otroke) v q
  • Odstranitev vozlišča iz vrste q

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Natisni sprednji del čakalne vrste in # ga odstrani iz čakalne vrste print (queue[0].data) node = queue.pop(0) # V čakalno vrsto postavi levega otroka, če node.left ni None: queue.append(node.left ) # V čakalno vrsto vnesite desni podrejeni element, če node.right ni None: queue.append(node.right) # Program gonilnika za preizkus zgornje funkcije root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print ('Prehod ravni vrstnega reda binarnega drevesa je -') printLevelOrder(root) 

Level Order Traversal of binary tree is - 1 2 3 4 5 

Časovna zahtevnost: O(n)

Več člankov o binarnem drevesu

• Vstavljanje v binarno drevo
• Izbris v binarnem drevesu
• Prehod po neurejenem drevesu brez rekurzije
• Inorder Tree Traversal brez rekurzije in brez sklada!
• Natisnite prehod po naročilu iz danih prehodov po vrstnem redu in prednaročilu
• Poiščite prehod BST po naročilu iz prehoda pred naročilom

Binarno iskalno drevo je binarna drevesna podatkovna struktura, ki temelji na vozliščih in ima naslednje lastnosti:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val  < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key) 

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val  < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r) 

20 30 40 50 60 70 80 

A graf je nelinearna podatkovna struktura, sestavljena iz vozlišč in robov. Vozlišča se včasih imenujejo tudi vozlišča, robovi pa so črte ali loki, ki povezujejo kateri koli dve vozlišči v grafu. Bolj formalno lahko graf definiramo kot graf, sestavljen iz končne množice vozlišč (ali vozlišč) in niza robov, ki povezujejo par vozlišč.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0 <=vtx <=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix()) 

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Program gonilnika za zgornji razred grafa, če je __name__ == '__main__' : V = 5 graph = Graph(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph() 

Adjacency list of vertex 0 head ->4 -> 1 Seznam sosednosti glave tocke 1 -> 4 -> 3 -> 2 -> 0 Seznam sosednosti glave tocke 2 -> 3 -> 1 Seznam sosednosti glave tocke 3 -> 4 -> 2 -> 1 Sosednost seznam vrhov 4 glave -> 3 -> 1 -> 0>>   
 Prehod grafa  
 
 Breadth-First Search ali BFS  
  
     Prehod v širino    za graf je podoben prehodu drevesa v širino. Edina težava pri tem je, da za razliko od dreves lahko grafi vsebujejo cikle, tako da lahko spet pridemo do istega vozlišča. Da bi se izognili večkratni obdelavi vozlišča, uporabimo logično obiskano matriko. Zaradi enostavnosti se predpostavlja, da so vsa oglišča dosegljiva iz začetnega oglišča.  
  
 Na primer, v naslednjem grafu začnemo prečkanje iz točke 2. Ko pridemo do točke 0, poiščemo vse sosednje točke. 2 je tudi sosednja vozlišča 0. Če ne označimo obiskanih vozlišč, bo 2 ponovno obdelan in bo postal proces brez zaključka. Prehod v širino naslednjega grafa je 2, 0, 3, 1.  
  
     
Python3   
# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2) 
    
  Izhod    Časovna kompleksnost: O(V+E), kjer je V število vozlišč v grafu, E pa število robov v grafu.  
  
 Depth First Search ali DFS  
 
   Prvo prečenje globine    za graf je podoben prvemu prehodu globine drevesa. Edina težava pri tem je, da za razliko od dreves lahko grafi vsebujejo cikle, vozlišče pa je mogoče obiskati dvakrat. Če se želite izogniti večkratni obdelavi vozlišča, uporabite logično obiskano matriko.  
  
    Algoritem:     
  
 
 Ustvarite rekurzivno funkcijo, ki vzame indeks vozlišča in obiskano matriko.  
 
 Označite trenutno vozlišče kot obiskano in natisnite vozlišče.  
 
 Prečkajte vsa sosednja in neoznačena vozlišča in pokličite rekurzivno funkcijo z indeksom sosednjega vozlišča.  
 
Python3   
# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2) 
    
  Izhod   
Following is DFS from (starting from vertex 2) 2 0 1 3 
  
 Več člankov o grafu  
 
 
  Predstavitve grafov z uporabo nabora in zgoščevanja   
 
  Poiščite matično oglišče v grafu   
 
  Iterativno iskanje po globini   
 
  Preštejte število vozlišč na dani ravni v drevesu z uporabo BFS   
 
  Preštejte vse možne poti med dvema vozliščema   
 
 
  Proces, v katerem funkcija neposredno ali posredno kliče samo sebe, se imenuje rekurzija, ustrezna funkcija pa se imenuje a    rekurzivna funkcija   . Z uporabo rekurzivnih algoritmov je mogoče nekatere probleme rešiti precej enostavno. Primeri takšnih težav so Hanojski stolpi (TOH), prehodi dreves po vrstnem redu/prednaročilu/naknadno, DFS grafa itd.   
   
 Kaj je osnovni pogoj v rekurziji?  
 
 V rekurzivnem programu je podana rešitev osnovnega primera, rešitev večjega problema pa je izražena z manjšimi problemi.  
  
def fact(n):  # base case  if (n  <= 1)   return 1  else   return n*fact(n-1) 
 
 V zgornjem primeru je definiran osnovni primer za n  <= 1 in večjo vrednost števila je mogoče rešiti s pretvorbo v manjšo, dokler ni dosežen osnovni primer.  
  
 Kako se pomnilnik dodeli različnim klicem funkcij v rekurziji?  
 
 Ko je katera koli funkcija poklicana iz main(), se ji dodeli pomnilnik v skladu. Rekurzivna funkcija pokliče samo sebe, pomnilnik za klicano funkcijo se dodeli poleg pomnilnika, dodeljenega klicni funkciji, in za vsak klic funkcije se ustvari drugačna kopija lokalnih spremenljivk. Ko je dosežen osnovni primer, funkcija vrne svojo vrednost funkciji, ki jo je poklicala, pomnilnik pa se sprosti in postopek se nadaljuje.  
  
 Vzemimo primer delovanja rekurzije s preprosto funkcijo.  
Python3   
# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test  < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test) 
    
  Izhod   
3 2 1 1 2 3 
  
 Pomnilniški sklad je prikazan na spodnjem diagramu.  
  
  
  
 Več člankov o rekurziji  
  
  
  Rekurzija   
  
     Rekurzija v Pythonu    
 
  Vadbena vprašanja za rekurzijo | Komplet 1   
 
  Vadbena vprašanja za rekurzijo | Komplet 2   
 
  Vadbena vprašanja za rekurzijo | Komplet 3   
 
  Vadbena vprašanja za rekurzijo | Komplet 4   
 
  Vadbena vprašanja za rekurzijo | Set 5   
 
  Vadbena vprašanja za rekurzijo | Komplet 6   
 
  Vadbena vprašanja za rekurzijo | Komplet 7   
 
 
     >>> Več      
  
    Dinamično programiranje     
 
   Dinamično programiranje    je predvsem optimizacija v primerjavi z navadno rekurzijo. Kjerkoli vidimo rekurzivno rešitev, ki ima ponavljajoče se klice za iste vnose, jo lahko optimiziramo z uporabo dinamičnega programiranja. Ideja je preprosto shraniti rezultate podproblemov, tako da nam jih pozneje ni treba znova izračunati, ko bo to potrebno. Ta preprosta optimizacija zmanjša časovno kompleksnost z eksponentne na polinomsko. Na primer, če napišemo preprosto rekurzivno rešitev za Fibonaccijeva števila, dobimo eksponentno časovno kompleksnost in če jo optimiziramo s shranjevanjem rešitev podproblemov, se časovna kompleksnost zmanjša na linearno.  
  
  
  
 Tabelariranje vs Memoizacija  
 
 Obstajata dva različna načina za shranjevanje vrednosti, tako da je mogoče vrednosti podproblema znova uporabiti. Tukaj bomo razpravljali o dveh vzorcih reševanja problema dinamičnega programiranja (DP):  
  
 
    Preglednica:     Od spodaj navzgor  
 
    Memoizacija:     Od zgoraj navzdol  
 
 
 Tabelacija  
 
 Kot že samo ime pove, začnite od spodaj in zbirajte odgovore na vrh. Pogovorimo se o tranziciji države.  
  
 Opišimo stanje za naš problem DP kot dp[x] z dp[0] kot osnovnim stanjem in dp[n] kot našim ciljnim stanjem. Torej moramo najti vrednost ciljnega stanja, tj. dp[n].  
  
 Če začnemo naš prehod iz našega osnovnega stanja, tj. dp[0], in sledimo našemu razmerju prehoda med stanjem, da dosežemo ciljno stanje dp[n], temu rečemo pristop od spodaj navzgor, saj je povsem jasno, da smo prehod začeli iz spodnje osnovno stanje in dosegel najvišje želeno stanje.  
  
 Zdaj, zakaj temu rečemo tabelarna metoda?  
  
 Da bi to vedeli, najprej napišimo kodo za izračun faktoriala števila s pristopom od spodaj navzgor. Kot naš splošni postopek za reševanje DP najprej definiramo stanje. V tem primeru definiramo stanje kot dp[x], kjer je dp[x] iskanje faktoriala x.  
  
 Zdaj je povsem očitno, da je dp[x+1] = dp[x] * (x+1)  
  
# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i 
 
 Memoizacija  
 
 Še enkrat, opišimo ga v smislu prehoda stanja. Če moramo najti vrednost za neko stanje, recite dp[n] in namesto da bi začeli z osnovnim stanjem, tj. dp[0], vprašamo svoj odgovor iz stanj, ki lahko dosežejo ciljno stanje dp[n] po prehodu stanja potem je to moda DP od zgoraj navzdol.  
  
 Tukaj začnemo naše potovanje od najvišjega ciljnega stanja in izračunamo njegov odgovor tako, da upoštevamo vrednosti stanj, ki lahko dosežejo ciljno stanje, dokler ne dosežemo najnižjega osnovnega stanja.  
  
 Še enkrat, napišimo kodo za faktorski problem na način od zgoraj navzdol  
  
# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1)) 
 
  
  
 Več člankov o dinamičnem programiranju  
 
 
  Optimalna lastnost podkonstrukcije   
 
  Lastnost prekrivajočih se podproblemov   
 
   Fibonaccijeva števila    
 
  Podmnožica z vsoto, deljivo z m   
 
  Največja vsota naraščajoče podzaporedje   
 
  Najdaljši skupni podniz   
 
 
      >>> Več       
  
 Iskalni algoritmi  
 
 Linearno iskanje  
 
 
 Začnite od skrajno levega elementa arr[] in enega za drugim primerjajte x z vsakim elementom arr[]  
 
 Če se x ujema z elementom, vrni indeks.  
 
 Če se x ne ujema z nobenim od elementov, vrnite -1.  
 
  
     
Python3   
# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result) 
    
  Izhod   
Element is present at index 3 
  
 Časovna kompleksnost zgornjega algoritma je O(n).  
  
 Za več informacij glejte   Linearno iskanje   .  
  
 Binarno iskanje  
 
 Poiščite razvrščeno matriko tako, da večkrat razdelite iskalni interval na pol. Začnite z intervalom, ki pokriva celotno polje. Če je vrednost iskalnega ključa manjša od postavke na sredini intervala, zožite interval na spodnjo polovico. V nasprotnem primeru ga zožite na zgornjo polovico. Večkrat preverite, dokler ni vrednost najdena ali pa je interval prazen.  
  
     
Python3   
# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Če je element prisoten na sami sredini if ​​arr[mid] == x: return mid # Če je element manjši od sredine, potem je # lahko le prisoten v levi podmatrici elif arr[mid]> x: vrni binarySearch(arr, l, mid-1, x) # Sicer je element lahko prisoten samo # v desni podmatrici else: vrni binarySearch(arr, mid + 1, r, x ) else: # Element ni prisoten v matriki return -1 # Koda gonilnika arr = [ 2, 3, 4, 10, 40 ] x = 10 # Rezultat klica funkcije = binarySearch(arr, 0, len(arr)-1 , x) če je rezultat != -1: natisni ('Element je prisoten pri indeksu % d' % rezultat) else: natisni ('Element ni prisoten v matriki') 
    
  Izhod   
Element is present at index 3 
  
 Časovna kompleksnost zgornjega algoritma je O(log(n)).  
  
 Za več informacij glejte    Binarno iskanje    .  
  
 Algoritmi za razvrščanje  
 
 Izbor Razvrsti  
 
 The    izbirna vrsta    algoritem razvrsti matriko tako, da večkrat poišče najmanjši element (glede na naraščajoči vrstni red) iz nerazvrščenega dela in ga postavi na začetek. V vsaki ponovitvi izbirnega razvrščanja se najmanjši element (glede na naraščajoči vrstni red) iz nerazvrščene podmatrike izbere in premakne v razvrščeno podmatriko.  
  
 Diagram poteka izbirnega razvrščanja:  
  
     
Python3   
# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Zamenjaj najdeni najmanjši element s # prvim elementom A[i], A[min_idx] = A[min_idx], A[i] # Koda gonilnika za preizkus nad tiskanjem ('Razvrščena matrika ') za i v območju (len(A)): print('%d' %A[i]), 
    
  Izhod   
Sorted array 11 12 22 25 64 
  
    Časovna zapletenost:     O(n   2   ), saj obstajata dve ugnezdeni zanki.  
  
    Pomožni prostor:     O(1)  
  
 Bubble Sort  
 
   Bubble Sort    je najpreprostejši algoritem za razvrščanje, ki deluje tako, da večkrat zamenja sosednje elemente, če so v napačnem vrstnem redu.  
  
    Ilustracija:     
  
     
Python3   
# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Koda gonilnika za preizkus nad arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Razvrščena matrika je:') za i v obsegu(len(arr)): print ('%d' %arr[i]), 
    
  Izhod   
Sorted array is: 11 12 22 25 34 64 90 
  
    Časovna zapletenost:     O(n   2   )  
  
 Razvrščanje vstavljanja  
 
 Za razvrščanje matrike velikosti n v naraščajočem vrstnem redu z uporabo    vrsta vstavljanja    :  
  
 
 Iteracija od arr[1] do arr[n] po matriki.  
 
 Primerjajte trenutni element (ključ) z njegovim predhodnikom.  
 
 Če je ključni element manjši od svojega predhodnika, ga primerjajte s prejšnjimi elementi. Premaknite večje elemente za en položaj navzgor, da naredite prostor za zamenjani element.  
 
 
    Ilustracija:     
  
     
Python3   
# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 in ključ < arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i]) 
    
  Izhod   
 5 6 11 12 13 
  
    Časovna zapletenost:     O(n   2   ))  
  
 Spoji Razvrsti  
 
 Tako kot QuickSort,    Spoji Razvrsti    je algoritem deli in vladaj. Vhodno matriko razdeli na dve polovici, se pokliče za obe polovici in nato združi dve razvrščeni polovici. Funkcija merge() se uporablja za spajanje dveh polovic. Merge(arr, l, m, r) je ključni postopek, ki predvideva, da sta arr[l..m] in arr[m+1..r] razvrščena in združi dve razvrščeni podmatriki v eno.  
  
MergeSort(arr[], l, r) If r>l 1. Poiščite srednjo točko za razdelitev matrike na dve polovici: sredina m = l+ (r-l)/2 2. Pokličite mergeSort za prvo polovico: Pokličite mergeSort(arr, l, m) 3. Pokličite mergeSort za drugo polovico: Pokličite mergeSort(arr, m+1, r) 4. Spojite dve polovici, razvrščeni v 2. in 3. koraku: Pokličite merge(arr, l, m, r) 
  
     
Python3   
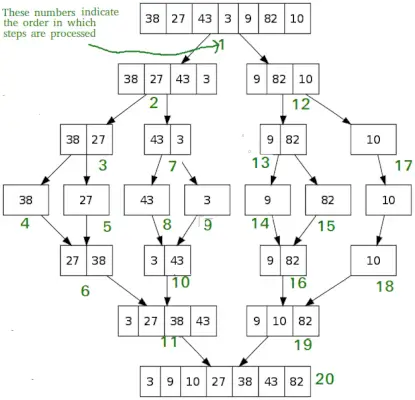
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Iskanje sredine matrike mid = len(arr)//2 # Razdelitev elementov matrike L = arr[:mid] # na 2 polovici R = arr[mid:] # Razvrščanje prve polovice mergeSort(L) # Razvrščanje druge polovice mergeSort(R) i = j = k = 0 # Kopiranje podatkov v začasni nizi L[] in R[], medtem ko i < len(L) and j  < len(R): if L[i]  < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i  < len(L): arr[k] = L[i] i += 1 k += 1 while j  < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr) 
    
  Izhod   
Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13 
  
    Časovna zapletenost:     O(n(log))  
  
 QuickSort  
 
 Kot Merge Sort,    QuickSort    je algoritem deli in vladaj. Izbere element kot vrtišče in razdeli dano matriko okoli izbranega vrtišča. Obstaja veliko različnih različic QuickSort, ki izberejo vrtišče na različne načine.  
  
 Za vrtišče vedno izberite prvi element.  
  
 
 Za vrtišče vedno izberi zadnji element (implementirano spodaj)  
 
 Za vrtišče izberite naključni element.  
 
 Izberite mediano kot vrtišče.  
 
 
 Ključni postopek v QuickSort je partition(). Cilj particij je, glede na matriko in element x matrike kot vrtišče, postaviti x na pravilno mesto v razvrščeni matriki in postaviti vse manjše elemente (manjše od x) pred x ter postaviti vse večje elemente (večje od x) za x. Vse to je treba narediti v linearnem času.  
  
/* low -->Začetni indeks, visoko --> Končni indeks */ quickSort(arr[], low, high) { if (low { /* pi je particijski indeks, arr[pi] je zdaj na pravem mestu */ pi = partition(arr, nizko, visoko); quickSort(arr, low, pi - 1); // Pred pi quickSort(arr, pi + 1, high); // Za pi } 
 
  
  
    Algoritem za razdelitev     
  
 Obstaja veliko načinov za razdelitev    psevdo koda    sprejme metodo iz knjige CLRS. Logika je preprosta, začnemo od skrajno levega elementa in sledimo indeksu manjših (ali enakih) elementov kot i. Če med prečkanjem najdemo manjši element, trenutni element zamenjamo z arr[i]. V nasprotnem primeru zanemarimo trenutni element.  
  
/* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ partition (arr[], low, high) {  // pivot (Element to be placed at right position)  pivot = arr[high];   i = (low – 1) // Index of smaller element and indicates the   // right position of pivot found so far  for (j = low; j  <= high- 1; j++){  // If current element is smaller than the pivot  if (arr[j]   i++; // increment index of smaller element  swap arr[i] and arr[j]  }  }  swap arr[i + 1] and arr[high])  return (i + 1) } 
Python3   
# Python3 implementation of QuickSort # This Function handles sorting part of quick sort # start and end points to first and last element of # an array respectively def partition(start, end, array): # Initializing pivot's index to start pivot_index = start pivot = array[pivot_index] # This loop runs till start pointer crosses # end pointer, and when it does we swap the # pivot with element on end pointer while start  < end: # Increment the start pointer till it finds an # element greater than pivot while start  < len(array) and array[start]  <= pivot: start += 1 # Decrement the end pointer till it finds an # element less than pivot while array[end]>pivot: end -= 1 # Če se začetek in konec nista prekrižala, # zamenjaj številki na začetku in koncu if(start < end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start  < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}') 
    
  Izhod   
Sorted array: [1, 5, 7, 8, 9, 10] 
  
    Časovna zapletenost:     O(n(log))  
  
 ShellSort  
 
  ShellSort   je v glavnem različica Insertion Sort. Pri razvrščanju z vstavljanjem premaknemo elemente samo eno mesto naprej. Ko je treba element premakniti daleč naprej, je vključenih veliko premikov. Ideja shellSort je omogočiti izmenjavo oddaljenih predmetov. V shellSort naredimo matriko h-razvrščeno za veliko vrednost h. Vrednost h znižujemo, dokler ne postane 1. Matrika je razvrščena po h, če so vsi podseznami vsakega h   th   element je razvrščen.  
Python3   
# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = vrzel # preveri matriko od leve proti desni # do zadnjega možnega indeksa j, medtem ko j < len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # zdaj pogledamo nazaj od i-tega indeksa na levo # zamenjamo vrednosti, ki niso v pravem vrstnem redu. k = i medtem ko k - vrzel> -1: če arr[k - vrzel]> arr[k]: arr[k-vrzel],arr[k] = arr[k],arr[k-vrzel] k ​​-= 1 vrzel //= 2 # gonilnik za preverjanje kode arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2) 
    
  Izhod   
input array: [12, 34, 54, 2, 3] sorted array [2, 3, 12, 34, 54] 
  
    Časovna zapletenost:     O(n   2   ).