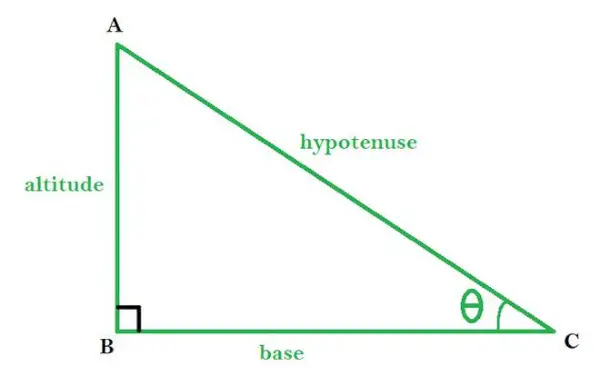
Trikotniki so tristrani zaprti mnogokotniki, ki jih tvori presečišče treh črt. V vsakdanjem življenju se veliko srečuje. Je ena od osnovnih oblik geometrije. Ima tri stranice, tri kote in tri oglišča. Pravokotni trikotnik je tisti, pri katerem je eden od kotov vedno enak 90°. Pitagorov izrek je izpeljan za pravokotne trikotnike, ki pravi, da je kvadrat hipotenuze (najdaljša stranica) enak vsoti kvadratov osnove in navpičnice.

Glede na dolžino vsaj dveh stranic pravokotnega trikotnika lahko poiščemo vrednost katerega koli kota pravokotnega trikotnika. Za to uporabljamo različne trigonometrične funkcije, kot so sinus, kosinus, tangens, kotangens, sec in cosec. Ti nam pomagajo povezati kote pravokotnega trikotnika z njegovimi stranicami.

Lastnosti

• Med tremi oglišči je pravokotno oglišče
• Stranico, ki je nasprotna pravokotnemu oglišču, imenujemo hipotenuza .
• Dolžina stranic sledi Pitagorovemu izreku, ki pravi

hipotenuza ² = osnova ² + nadmorska višina ²

• Hipotenuza je najdaljša stranica pravokotnega trikotnika.
• Koti, razen pravega kota, so ostri koti, saj je vrednost manjša od 90 ^O

Trigonometrične funkcije

ABC je pravokoten trikotnik z ∠B kot pravim kotom

• cosθ: To daje razmerje med osnovo in hipotenuzo pravokotnega trikotnika.

cosθ = osnova / hipotenuza

• sinθ: To daje razmerje nadmorske višine s hipotenuzo pravokotnega trikotnika.

sinθ = nadmorska višina / hipotenuza

• tanθ: Je razmerje med nadmorsko višino in osnovo pravokotnega trikotnika.

tanθ = nadmorska višina / osnova

• posteljicaθ: Je inverzna tanθ
• secθ: Je obratna vrednost cosθ
• cosecθ: Je inverzna sinθ

Da bi našli kote pravokotnega trikotnika, lahko vzamemo trigonometrično obratno razmerje danih stranic trikotnika.

primer:

Če je sinθ = x, potem lahko zapišemo

θ = sin ^-1 x.

To vrne kot, za katerega je sinusna vrednost kota x.

Podobno obstaja cos ^-1 θ, torej ^-1 jaz, posteljica ^-1 θ, sekunda ^-1 θ in cosec ^-1 jaz

Vzorčne težave

Vprašanje 1. Podan je pravokoten trikotnik, katerega osnova je 10 cm in hipotenuza 20 cm. Poiščite vrednost osnovnega kota.

rešitev:

Podano, osnova = 10 cm

Hipotenuza = 20 cm

Naj bo vrednost osnovnega kota θ. Lahko pišemo

cosθ = osnova / hipotenuza = 10/20 = 1/2

θ = cos ^-1 (1/2) = 60 ^O

Tako je vrednost osnovnega kota 60 ^O .

Vprašanje 2. Poiščite vrednost kotov pravokotnega trikotnika, glede na to, da je eden od ostrih kotov dvakrat večji od drugega.

rešitev:

Ker vemo, da je vsota vseh treh kotov v trikotniku 180 ^O .

Ker je eden od kotov 90 ^O in je eden od ostrih kotov dvakrat večji od drugega, jih lahko obravnavamo kot θ in 2θ.

Torej, lahko pišemo

90 ^O + θ + 2θ = 180 ^O

3θ = 180 ^O – 90 ^O

3θ = 90 ^O

θ = 90 ^O /3 = 30 ^O

2θ = 2 × 30 ^O = 60 ^O

Torej, koti so 30 ^O , 60 ^O , in 90 ^O .

Vprašanje 3. Poiščite vrednost kota višine lestve dolžine 5 m, glede na to, da je osnova lestve na razdalji 3 m od stene.

rešitev:

Ker lestev deluje kot hipotenuza pravokotnega trikotnika in je osnovna razdalja enaka 3 m, lahko zapišemo

Hipotenuza = 5m

Osnova = 3m

Naj bo višinski kot θ. Torej, lahko pišemo

cosθ = osnova / hipotenuza = 3/5

θ = cos ^-1 (3/5)

θ = 53 ^O

Tako je vrednost kota višine 53 ^O .

Vprašanje 4. Poiščite vrednost hipotenuze, če je dolžina nadmorske višine 8 m in osnovni kot 30 ^O .

rešitev:

Glede na osnovni kot je enak 30 ^O in je nadmorska višina enaka 8 m, lahko za iskanje dolžine hipotenuze uporabimo funkcijo sinusa.

greh30 ^O = nadmorska višina / hipotenuza

hipotenuza = nadmorska višina / sin30 ^O

Ker je vrednost sin30 ^O je enako 1/2, lahko zapišemo

hipotenuza = nadmorska višina / (1/2) = 2 × nadmorska višina

Tako je hipotenuza = 2 × 8 = 16 m

Tako je dolžina hipotenuze enaka 16 m.