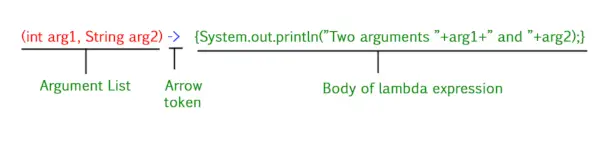
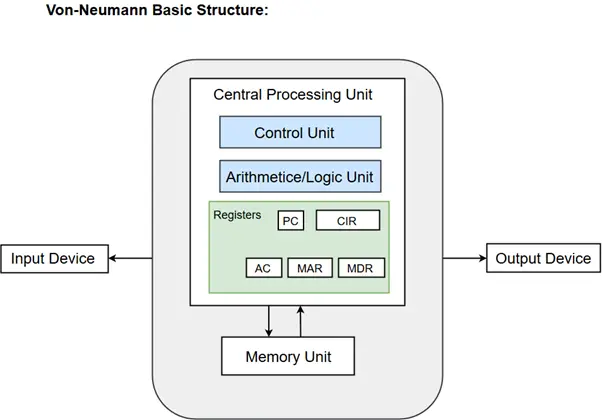
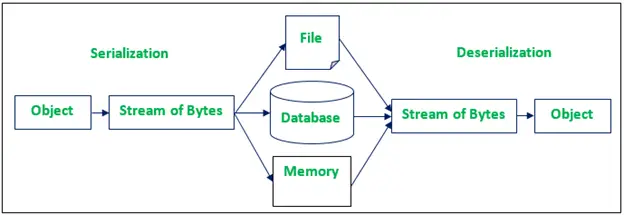
Formula a2 – b2

a 2 – b 2 formula v Algebra je osnovna formula v matematiki, ki se uporablja za reševanje različnih algebrskih problemov. a 2 – b 2 formula se imenuje tudi razlika kvadrata formula, saj nam ta formula pomaga najti razliko med dvema kvadratoma, ne da bi dejansko izračunala kvadrata. Spodnja slika prikazuje formulo a 2 – b 2

V tem članku se bomo naučili a 2 – b 2 formula, a 2 – b 2 identiteto, primere in druge podrobnosti.
Kazalo
- Kaj je formula a2 – b2?
- Razlika v formuli kvadratov
- Dokaz kvadratne formule a2 – b2
- Formula (a + b)2 in (a – b)2
- a2 – b2 Identiteta
Kaj je a 2 – b 2 Formula?
a 2 – b 2 formula v algebri je osnovna formula za reševanje algebrskih problemov. Uporablja se tudi za reševanje trigonometričnih, diferencialnih in drugih problemov. Ta formula nam pove, da je razlika med kvadratom dveh števil enaka produktu vsote in razlike dveh števil, tj.
a 2 – b 2 = (a + b). (a – b)
a 2 – b 2 Definicija formule
Formula a 2 – b 2 nam omogoča, da določimo varianco med kvadratoma dveh števil, ne da bi morali izračunati dejanske kvadratne vrednosti. Izraz za a 2 – b 2 formula je naslednja: a 2 – b 2 = (a + b). (a – b)
Razlika v formuli kvadratov
Razlika dveh kvadratov se izračuna z uporabo standardne algebraične identitete a 2 – b 2 . Na primer, dani sta nam dve spremenljivki, a in b, razlika njunih kvadratov pa se izračuna z uporabo formule, a 2 – b 2 = (a+b).(a–b)
V bistvu formula razlike kvadratov pravi, da je za kateri koli dve algebraični spremenljivki a in b izraz a 2 – b 2 je enak produktu vsote in razlike spremenljivk. Ta identiteta se pogosto uporablja za poenostavitev zapletenih algebrskih izrazov.
a 2 – b 2 Dokaz kvadratne formule
a 2 – b 2 identiteto je mogoče dokazati s poenostavitvijo RHS identitete. A 2 – b 2 formula je podana kot,
a 2 – b 2 = (a – b)(a + b)
Ta formula je dokazana kot,
RHS = (a+b) (a–b)
⇒ RHS = a (a–b) + b (a–b)
⇒ RHS = a 2 – ab + ba – b 2
⇒ RHS = a 2 – ab + ab – b 2
⇒ RHS = a 2 – b 2
⇒ RHS = LHS
Zato dokazano.
a 2 + b 2 Formula
A 2 + b 2 formula je algebraična formula, ki se uporablja za iskanje vsote kvadratov dveh števil. Vsota kvadratne formule je podana kot
a 2 + b 2 = (a + b) 2 – 2ab
A 2 + b 2 Formula se uporablja za reševanje različnih algebrskih problemov. Spodaj so dodane različne druge pomembne algebraične formule,
(a + b) 2 in (a – b) 2 Formula
(a + b) 2 formula je podana kot,
(a + b) 2 = a 2 + b 2 + 2ab
(a – b) 2 formula je podana kot,
(a – b) 2 = a 2 + b 2 – 2ab
a 2 – b 2 Identiteta
a 2 – b 2 identiteta je ena od algebraične identitete ki se uporablja za iskanje razlike med kvadratoma dveh števil. Ta identiteta ima različne aplikacije in je dana kot,
a 2 – b 2 = (a – b).(a + b)
Preberi več,
- Formula algebre
- Osnovna matematična formula
- Algebrični izraz
Primeri na a 2 – b 2 Formula
Primer 1: Poenostavite x 2 – 16
rešitev:
= x 2 – 16
= x 2 - 4 2
Vemo, da a 2 – b 2 = (a+b) (a–b)
podano,
- a = x
- b = 4
= (x + 4) (x – 4)
Primer 2: Poenostavite 9y 2 – 144
rešitev:
= 9 let 2 – 144
= (3 leta) 2 – (12) 2
Vemo, da a 2 – b 2 = (a+b)(a–b)
podano,
- a = 3y
- b = 12
= (3y + 12)(3y – 12)
Primer 3: Poenostavitev (3x + 2) 2 – (3x – 2) 2
rešitev:
Vemo, da
a 2 – b 2 = (a+b)(a–b)
podano,
- a = 3x + 2
- b = 3x – 2
(3x + 2) 2 – (3x – 2) 2
= (3x + 2 + 3x – 2)(3x + 2 – (3x – 2))
= 6x (3x + 2 – 3x + 2)
= 6x(4)
= 24x
Primer 4: Poenostavite in 2 – 100
rešitev:
= in 2 – 100
= in 2 – (10) 2
Vemo, da
a 2 – b 2 = (a+b)(a–b)
podano,
- a = in
- b = 10
= (y + 10) (y – 10)
Primer 5: Ocenite (x + 6) (x – 6)
rešitev:
Vemo, da
(a+b) (a–b) = a 2 – b 2
podano,
- a = x
- b = 6
(x + 6) (x – 6)
= x 2 – 6 2
= x 2 – 36
Primer 6: Ocenite (y + 13) (y – 13)
rešitev:
Vemo, da
(a+b) (a–b) = a 2 – b 2
podano,
- a = in
- b = 13
(y + 13). (y – 13)
= in 2 – (13) 2
= in 2 – 169
Primer 7: Vrednotenje (x + y + z). (x + y – z)
rešitev:
Vemo, da
(a+b) (a–b) = a 2 – b 2
podano,
- a = x + y
- b = z
(x + y + z) (x + y – z)
= (x + y) 2 - Z 2
= x 2 + in 2 + 2xy – z 2
(a 2 – b 2 ) Formula – delovni list
Q1. Poenostavite 15 2 – 14 2 z uporabo a 2 – b 2 identiteta.
Q2. Poenostavite 11 2 – 7 2 z uporabo a 2 – b 2 identiteta.
Q3. Reši 23 2 – 9 2 z uporabo a 2 – b 2 identiteta.
Q4. Reši 9 2 – 7 2 z uporabo a 2 – b 2 identiteta.
a 2 – b 2 Formula – pogosta vprašanja
1. Kaj je a 2 − b 2 ?
a 2 – b 2 formula je formula, ki se uporablja za iskanje razlike med dvema kvadratoma, ne da bi dejansko našli kvadrat. A 2 – b 2 formula je,
a 2 – b 2 = (a + b)(a – b)
2. Kaj je zakon a 2 b 2 Formula?
Zakon o a 2 b 2 formule so,
- a 2 – b 2 = (a + b)(a – b)
- a 2 + b 2 = (a + b) 2 – 2ab
3. Kaj je a 2 b 2 Formula, ki se uporablja za?
a 2 b 2 formula se uporablja za reševanje različnih algebrskih problemov, uporabljajo pa se tudi za poenostavitev trigonometričnih, računskih in integracijskih problemov.
4. Kaj je a 2 b 2 Formula?
Obstajata dva a 2 b 2 formule, ki so, a 2 + b 2 in a 2 – b 2 razširitvena formula za a 2 b 2 formule so podane kot,
- a 2 – b 2 = (a + b)(a – b)
- a 2 + b 2 = (a + b) 2 – 2ab
5. Kdaj je a 2 – b 2 Formula se uporablja?
a 2 – b 2 formula se uporablja za iskanje razlike med kvadratoma dveh števil, ne da bi dejansko našli kvadrata. Ta formula se uporablja tudi za reševanje različnih algebrskih, trigonometričnih in drugih problemov.