Čas potrebný na stretnutie v rovnostrannom trojuholníku
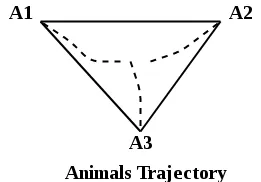
Pri danej dĺžke strán rovnostranného trojuholníka (s) a rýchlostiach (v) každého zvieraťa označeného na vrcholoch trojuholníka zistite čas, po ktorom sa stretnú, ak sa začnú pohybovať smerom k svojmu pravému protikladu a tvoria trajektóriu.

Príklady:
Vstup: s = 2 v = 5
výstup: 0,266667Vstup: s = 11 v = 556
výstup: 0,013189
prístup:
Ak chcete zistiť celkové množstvo času potrebného na stretnutie zvierat, jednoducho vezmite A delené počiatočnou rýchlosťou, ktorou sa dva vrcholy k sebe približujú. Vyberte ľubovoľné dva vrcholy a uvidíte, že prvý bod sa pohybuje v smere k druhému rýchlosťou v, zatiaľ čo druhý sa pohybuje v smere k prvému (stačí vziať komponent pozdĺž jednej z hrán trojuholníka).
Referencia : StackExchange
Nižšie je uvedená implementácia vyššie uvedeného prístupu:
C++ // CPP code to find time // taken by animals to meet #include using namespace std ; // function to calculate time to meet void timeToMeet ( double s double v ){ double V = 3 * v / 2 ; double time = s / V ; cout < < time ; } // Driver Code int main ( void ) { double s = 25 v = 56 ; timeToMeet ( s v ); return 0 ; }
Java // Java code to find time taken by animals // to meet import java.io.* ; public class GFG { // function to calculate time to meet static void timeToMeet ( double s double v ){ double V = 3 * v / 2 ; double time = s / V ; System . out . println (( float ) time ); } // Driver Code static public void main ( String [] args ) { double s = 25 v = 56 ; timeToMeet ( s v ); } } //This code is contributed by vt_m.
Python3 # Python3 code to find time # taken by animals to meet # function to calculate # time to meet def timeToMeet ( s v ): V = 3 * v / 2 ; time = s / V ; print ( time ); # Driver Code s = 25 ; v = 56 ; timeToMeet ( s v ); # This code is contributed by mits
C# // C# code to find time // taken by animals to meet using System ; public class GFG { // function to calculate time to meet static void timeToMeet ( double s double v ){ double V = 3 * v / 2 ; double time = s / V ; Console . WriteLine (( float ) time ); } // Driver Code static public void Main () { double s = 25 v = 56 ; timeToMeet ( s v ); } } // This code is contributed by vt_m.
PHP // PHP code to find time // taken by animals to meet // function to calculate // time to meet function timeToMeet ( $s $v ) { $V = 3 * $v / 2 ; $time = $s / $V ; echo $time ; } // Driver Code $s = 25 ; $v = 56 ; timeToMeet ( $s $v ); // This code is contributed by anuj_67. ?>
JavaScript < script > // JavaScript code to find time taken by animals // to meet // function to calculate time to meet function timeToMeet ( s v ) { var V = 3 * v / 2 ; var time = s / V ; document . write ( time . toFixed ( 6 )); } // Driver Code var s = 25 v = 56 ; timeToMeet ( s v ); // This code is contributed by todaysgaurav < /script>
Výstup
0.297619
Časová zložitosť: O(1)
Pomocný priestor: O(1)