Multiplexer

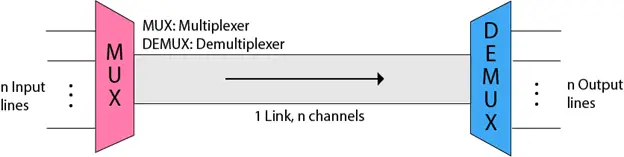
Multiplexer je kombinovaný obvod, ktorý má 2 n vstupné riadky a jeden výstupný riadok. Jednoducho, multiplexor je viacvstupový a jednovýstupový kombinovaný obvod. Binárne informácie sú prijímané zo vstupných liniek a smerované do výstupnej linky. Na základe hodnôt výberových riadkov bude jeden z týchto dátových vstupov pripojený k výstupu.
Na rozdiel od kodéra a dekodéra existuje n výberových riadkov a 2 n vstupné riadky. Celkovo sú teda 2 N možné kombinácie vstupov. S multiplexerom sa tiež zaobchádza ako Mux .
Existujú rôzne typy multiplexerov, ktoré sú nasledovné:
2×1 multiplexer:
V multiplexeri 2×1 sú len dva vstupy, t.j. A 0 a A 1 , 1 riadok výberu, t.j. S 0 a jednotlivé výstupy, t.j. Y. Na základe kombinácie vstupov, ktoré sú prítomné na výberovom riadku S 0 , jeden z týchto 2 vstupov bude pripojený k výstupu. Bloková schéma a pravdivostná tabuľka 2 × 1 multiplexer sú uvedené nižšie.
Bloková schéma:

Tabuľka pravdy:

Logické vyjadrenie výrazu Y je nasledovné:
Y=S 0 '.A 0 +S 0 .A 1
Logický obvod vyššie uvedeného výrazu je uvedený nižšie:

4×1 multiplexer:
V multiplexeri 4×1 sú celkom štyri vstupy, teda A 0 , A 1 , A 2 a A 3 , 2 výberové riadky, t.j. S 0 a S 1 a jeden výstup, t.j. Y. Na základe kombinácie vstupov, ktoré sú prítomné na výberových riadkoch S 0 a S 1 , jeden z týchto 4 vstupov je pripojený k výstupu. Bloková schéma a pravdivostná tabuľka 4 × 1 multiplexer sú uvedené nižšie.
Bloková schéma:

Tabuľka pravdy:

Logické vyjadrenie výrazu Y je nasledovné:
Y=S 1 'S 0 'A 0 +S 1 'S 0 A 1 +S 1 S 0 'A 2 +S 1 S 0 A 3
Logický obvod vyššie uvedeného výrazu je uvedený nižšie:

Multiplexer 8 na 1
V multiplexeri 8 na 1 je celkovo osem vstupov, t.j. A 0 , A 1 , A 2 , A 3 , A 4 , A 5 , A 6 a A 7 , 3 výberové riadky, t.j. S 0 , S 1 a S 2 a jeden výstup, t.j. Y. Na základe kombinácie vstupov, ktoré sú prítomné na výberových riadkoch S 0 , S 1, a S 2 , jeden z týchto 8 vstupov je pripojený k výstupu. Bloková schéma a pravdivostná tabuľka 8 × 1 multiplexer sú uvedené nižšie.
Bloková schéma:

Tabuľka pravdy:

Logické vyjadrenie výrazu Y je nasledovné:
Y=S 0 '.S 1 '.S 2 '.A 0 +S 0 .S 1 '.S 2 '.A 1 +S 0 '.S 1 .S 2 '.A 2 +S 0 .S 1 .S 2 '.A 3 +S 0 '.S 1 '.S 2 A 4 +S 0 .S 1 '.S 2 A 5 +S 0 '.S 1 .S 2 .A 6 +S 0 .S 1 .S 3 .A 7
Logický obvod vyššie uvedeného výrazu je uvedený nižšie:

8 × 1 multiplexer využívajúci 4 × 1 a 2 × 1 multiplexer
Môžeme implementovať 8 × 1 multiplexer s použitím multiplexora nižšieho rádu. Na implementáciu 8 × 1 multiplexer, potrebujeme dva 4 × 1 multiplexer a jeden 2 × 1 multiplexer. 4 × 1 multiplexor má 2 výberové riadky, 4 vstupy a 1 výstup. 2 × 1 multiplexor má iba 1 výberový riadok.
Na získanie 8 dátových vstupov potrebujeme dva 4 × 1 multiplexery. 4 × 1 multiplexor vytvára jeden výstup. Takže, aby sme získali konečný výstup, potrebujeme 2 × 1 multiplexer. Bloková schéma z 8 × 1 multiplexer pomocou 4 × 1 a 2 × 1 multiplexer je uvedený nižšie.

16 na 1 multiplexer
V multiplexeri 16 ku 1 je celkovo 16 vstupov, t.j. 0 , A 1 , …, A 16 , 4 výberové riadky, t.j. S 0 , S 1 , S 2 a S 3 a jeden výstup, t.j. Y. Na základe kombinácie vstupov, ktoré sú prítomné na výberových riadkoch S 0 , S 1 a S 2 , jeden z týchto 16 vstupov bude pripojený k výstupu. Bloková schéma a pravdivostná tabuľka 16 × 1
Bloková schéma:

Tabuľka pravdy:

Logické vyjadrenie výrazu Y je nasledovné:
Y=A 0 .S 0 '.S 1 '.S 2 '.S 3 '+A 1 .S 0 '.S 1 '.S 2 '.S 3 +A 2 .S 0 '.S 1 '.S 2 .S 3 '+A 3 .S 0 '.S 1 '.S 2 .S 3 +A 4 .S 0 '.S 1 .S 2 '.S 3 '+A 5 .S 0 '.S 1 .S 2 '.S 3 +A 6 .S 1 .S 2 .S 3 '+A 7 .S 0 '.S 1 .S 2 .S 3 +A 8 .S 0 .S 1 '.S 2 '.S 3 '+A 9 .S 0 .S 1 '.S 2 '.S 3 +Y 1 0.S 0 .S 1 '.S 2 .S 3 '+A 1 1.S 0 .S 1 '.S 2 .S 3 +A 1 2 S 0 .S 1 .S 2 '.S 3 '+A 1 3.S 0 .S 1 .S 2 '.S 3 +A 1 4.S 0 .S 1 .S 2 .S 3 '+A 1 5.S 0 .S 1 .S 2 '.S 3Logický obvod vyššie uvedeného výrazu je uvedený nižšie:

16×1 multiplexer využívajúci 8×1 a 2×1 multiplexer
Môžeme implementovať 16 × 1 multiplexer s použitím multiplexora nižšieho rádu. Na implementáciu 8 × 1 multiplexer, potrebujeme dva 8 × 1 multiplexer a jeden 2 × 1 multiplexer. 8 × 1 multiplexor má 3 výberové riadky, 4 vstupy a 1 výstup. 2 × 1 multiplexor má iba 1 výberový riadok.
Na získanie 16 dátových vstupov potrebujeme dva 8×1 multiplexory. 8 × 1 multiplexor vytvára jeden výstup. Takže, aby sme získali konečný výstup, potrebujeme 2 × 1 multiplexer. Bloková schéma zo 16 × 1 multiplexer s použitím 8 × 1 a 2 × 1 multiplexer je uvedený nižšie.