Algebraické pojmy ako a na rozdiel od nich: definícia a príklady
Podobné výrazy sú výrazy v algebraických výrazoch, ktoré majú rovnaké premenné umocnené na rovnakú mocninu. Pojmy podobné a odlišné sú typy výrazov v algebre a môžeme rozlišovať medzi podobnými a odlišnými výrazmi jednoduchou kontrolou premenných a ich právomocí. Algebraické členy definujeme ako jednotlivé členy získané z algebraickej rovnice.

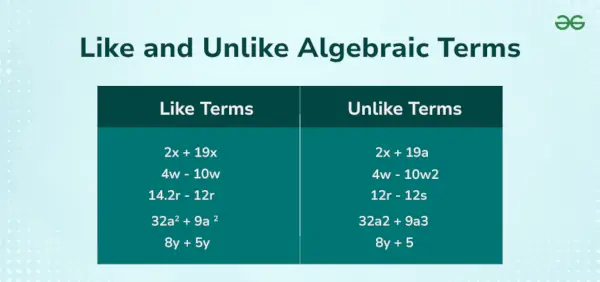
Napríklad v algebraickej rovnici 5x + 3r 2 = 12 máme tri pojmy, ktoré sú, 5x, 3y², a 12 . Tu, 5x, a 3r 2 sú variabilné členy a 12 je konštantný člen. Nasledujúci obrázok zobrazuje podobné a rozdielne výrazy.
V tomto článku sa podrobne dozvieme o podobných výrazoch, na rozdiel od výrazov, ich príkladoch, zjednodušení a iných.
Ako Podmienky
Podobné výrazy sú výrazy, ktoré majú rovnaké premenné a sila každej z premenných je tiež rovnaká. Môžeme kombinovať podobné výrazy, aby sme zjednodušili algebraické výrazy, a to sa dá veľmi ľahko vypočítať. Napríklad 3y + 5y je algebraický výraz s podobnými výrazmi 3y a 5y. Aby sme tento algebraický výraz zjednodušili, pridávame podobné výrazy. Teda zjednodušenie daného výrazu je 8y.
Príklady výrazov Páči sa mi
Podobne ako výrazy sú výrazy, ktoré majú rovnakú premennú s podobnou mocnosťou. Niektoré príklady podobných výrazov sú napr.
- 40xy 2 a 56xy 2 : V prvom príklade xy 2 je spoločný koeficient pre oba pojmy. Sú to teda ako pojmy.
- 30z 2 a 18z 2 : S 2 je spoločný koeficient pre oba pojmy. Sú to teda ako pojmy.
- 45abc a 29abc: abc je spoločný koeficient pre oba pojmy. Sú to teda ako pojmy.
- 18r 3 a 38r 3 : r 3 je spoločný koeficient pre oba pojmy. Sú to teda ako pojmy.
- 2xy a 8xy: xy je spoločný koeficient pre oba členy. Sú to teda ako pojmy.
Sčítanie a odčítanie podobných výrazov
Môžeme ľahko vykonávať sčítanie a odčítanie podobných výrazov a nevyžaduje to žiadne špeciálne pravidlo, zvyčajne sa zjednodušujú pomocou bežných pravidiel sčítania a odčítania. Tento koncept môžeme pochopiť pomocou nasledujúceho príkladu.
Príklad: Zjednodušte 11x 3 + 5x 3
Riešenie:
Ako vidíme, sú to podobné pojmy, pretože majú podobné premenné a ich sila je tiež konštantná.
Tieto výrazy môžeme jednoducho pridať priamo.
= 11x 3 + 5x 3
= 16x 3
Je to možné, pretože majú rovnaké premenné s podobnou silou a možno to chápať tak, že môžeme priamo pripočítať rupie k rupiám, t.j. 5 Rs + 7 Rs je 12 Rs. Ale nemôžeme priamo pridať rupie s dolármi a 5 Rs + 7 dolárov nemožno priamo zjednodušiť.
Podobne môžeme podobné výrazy aj priamo odčítať, len pridať, pridať podobné výrazy, čo možno pochopiť na nasledujúcom príklade.
Príklad 1: Zjednodušte 11x 3 – 5x 3
Riešenie:
Ako vidíme, sú to podobné pojmy, pretože majú podobné premenné a ich sila je tiež konštantná.
Tieto výrazy môžeme jednoducho priamo odčítať.
= 11x 3 – 5x 3
= 6x 3
Príklad 2: Pridajte 3 X + 2 a + 5 a 4 X − 3 a + 7.
Riešenie:
(3 X + 2 a + 5) + (4 X − 3 a + 7)
= (3 X + 4x) +(2r + (-3r))+ (5 + 7)
= 7 X − a + 12
Na rozdiel od podmienok
Na rozdiel od výrazov sú výrazy s rôznymi premennými a každá z premenných môže alebo nemusí mať na sebe rôzne exponenty. Napríklad 9x + 6y je algebraický výraz s na rozdiel od výrazov. Pretože má dve rôzne premenné x a y.
Ak sú premenné rôzne, nekontrolujeme moc, pretože sa v žiadnom prípade nelíšia od pojmov, ale ak sú premenné rovnaké, kontrolujeme ich mocniny, pretože sa môžu, ale nemusia podobať pojmom.
Napríklad 5x 2 a 6x 2 sú ako výrazy, ale 5x 2 a 6x 3 sú odlišné od pojmov.
Príklady výrazov na rozdiel od výrazov
Na rozdiel od termínov sú termíny, ktoré nemajú rovnaké premenné ani podobnú silu. Niektoré príklady odlišných výrazov sú,
- 40xy 2 a 56xy: Tu je v jednom algebraickom výraze premenná xy 2 a v druhom algebraickom výraze je premenná xy. Obe premenné sú rovnaké, ale majú rozdielne sily. Sú teda odlišné od pojmov.
- 45abc a 29ab: Tu je v jednom algebraickom výraze premenná abc a v druhom algebraickom výraze je premenná ab. Obe premenné sú odlišné. Na rozdiel od pojmov teda spadajú do kategórie.
Sčítanie a odčítanie odlišných výrazov
Sčítanie a odčítanie sa medzi pojmami na rozdiel od pojmov nevykonáva, t. j. nemôžeme sčítať ani odčítať na rozdiel od pojmov a dá sa to pochopiť na príklade, že k 6 kg ryže nemôžeme pridať 5 litrov mlieka. Rovnakým spôsobom nemôžeme na rozdiel od pojmov pridávať ani uberať.
Napríklad 3xy + 5x sa nedá ďalej riešiť a necháva sa to rovnako.
Rozdiel medzi podobnými výrazmi a odlišnými výrazmi
Rozdiely medzi podobnými a rozdielnymi výrazmi sú uvedené v tabuľke nižšie.
| Funkcia | Ako Podmienky | Na rozdiel od podmienok |
|---|---|---|
| Definícia | Podobné výrazy sú výrazy, ktoré majú rovnaké premenné a rovnaké hodnoty exponentov. | Na rozdiel od termínov sú termíny, ktoré majú rôzne premenné a exponenty. |
| Zjednodušenie | Podobné výrazy môžeme ľahko zjednodušiť. | Na rozdiel od pojmov, ktoré sa nedajú zjednodušiť. |
| Kombinovanie pojmov | Podobné výrazy je možné priamo kombinovať, aby sa vytvoril výpočet. | Na rozdiel od výrazov sa nedajú priamo kombinovať, pretože predstavujú rôzne množstvá |
| Sčítanie alebo odčítanie | Sčítanie a odčítanie je možné dosiahnuť podobnými výrazmi. | Na rozdiel od výrazov nemôžeme pridávať ani uberať. |
| Príklady | Príkladmi podobných výrazov sú x 2 , 5x 2 , -11/3x 2 , atď. | Príkladmi výrazov na rozdiel od typu sú x 2 a 5x 3 , -11/3x atď. |
Čítaj viac
- Algebraické výrazy
- Typy algebraických výrazov
Príklady algebrických výrazov Páči sa mi a Na rozdiel od neho
Príklad 1: Identifikujte podobné a odlišné výrazy z: 3x, 5xy, 18x 2 a 5x 3 , 29xy, 50x 3
Riešenie:
Výrazy Páči sa mi a Na rozdiel od daných výrazov sú,
Páči sa mi podmienky: (5xy, 29xy) a (5x 3 , 50x 3 )
Na rozdiel od podmienok: 3x, 18x 2 a
Príklad 2: Zjednodušte 3xy + 5x 2 + 11ab – 4xy
Riešenie:
Daný výraz: 3xy + 5x 2 + 11ab – 4xy
Podobne ako výraz v danom výraze, 3xy a -4xy
Pri zjednodušovaní,
= 3xy – 4xy + 5x 2 + 11ab
= -xy + 5x 2 + 11ab
Všetky výrazy sú odlišné od výrazov, takže ich nemožno ďalej riešiť.
Príklad 3: Zjednodušte 8x + 15x 2 + 11x – 4x 2
Riešenie:
Daný výraz: 8x + 15x 2 + 11x – 4x 2
Podobný výraz v danom výraze, (8x, 11x) a (15x 2 , -4x 2 )
Pri zjednodušovaní,
= 8x + 11x + 15x 2 – 4x 2
= 19x – 11x 2
Všetky výrazy sú odlišné od výrazov, takže ich nemožno ďalej riešiť.
Algebraické výrazy páči sa mi a na rozdiel od nich – často kladené otázky
Čo sú algebraické pojmy?
Algebraické členy sú jednotlivé členy získané z algebraickej rovnice, t. j. členy delené operačnými symbolmi ako + a -.
Aké sú výrazy páči sa mi a aké sú odlišné?
Podobné a rozdielne termíny sú termíny algebraického výrazu. Podobne máme podobné premenné a sila exponentu je rovnaká, zatiaľ čo v rozdielnych pojmoch sú premenné a ich moc rozdielne.
Aký je rozdiel medzi podobnými a odlišnými algebraickými výrazmi?
Základný rozdiel medzi podobnými a rozdielnymi výrazmi je v tom, že v podobnom výraze máme rovnakú premennú s rovnakými právomocami, zatiaľ čo na rozdiel od výrazov máme rôzne premenné s rôznymi právomocami.
Ako nájsť algebraické výrazy Páči sa mi a Na rozdiel od neho?
Podobné výrazy sú výrazy, ktoré majú rovnaké premenné s rovnakými mocnosťami, a rozdielne výrazy sú výrazy s rôznymi premennými a rôznymi mocnosťami a môžeme ich ľahko identifikovať len preskúmaním premenných.
Môžeme sčítať alebo odčítať ako algebraické výrazy?
Môžeme jednoducho pridať alebo odčítať, ako sú výrazy ako 5x a 11x ako výrazy a možno ich pripočítať ako 16x.
Môžeme pridať alebo odčítať na rozdiel od algebraických výrazov?
Na rozdiel od výrazov ako 2x a 3y nemôžeme pridávať ani uberať. Na rozdiel od výrazov sa teda nedajú sčítať ani odčítať spolu.