DISKRÉTNE MATEMATICKÉ MRIEŽKY - DISKRÉTNA MATEMATIKA

Nech L je neprázdna množina uzavretá pod dvomi binárnymi operáciami zvanými meet and join, označenými ∧ a ∨. Potom sa L nazýva mriežka, ak platia nasledujúce axiómy, kde a, b, c sú prvky v L:

1) Komutatívny zákon: -
(a) a ∧ b = b ∧ a (b) a ∨ b = b ∨ a

2) Asociačný zákon: -
(a) (a ∧ b)∧ c = a ∧(b∧ c) (b) (a ∨ b) ∨ c = a ∨ (b ∨ c)

3) Absorpčný zákon: -
(a) a ∧ ( a ∨ b) = a (b) a ∨ ( a ∧ b) = a

Dualita:

Duál ľubovoľného výroku v mriežke (L,∧ ,∨ ) je definovaný ako výrok, ktorý sa získa zámenou ∧ an ∨.

Napríklad , duál a ∧ (b ∨ a) = a ∨ a je a ∨ (b ∧ a )= a ∧ a

Ohraničené mriežky:

Mriežka L sa nazýva ohraničená mriežka, ak má najväčší prvok 1 a najmenší prvok 0.

Príklad:

Množina P(S) množiny S pri operáciách prieniku a zjednotenia je ohraničená mriežka, pretože ∅ je najmenší prvok P(S) a množina S je najväčší prvok P(S).
Množina +ve celé číslo I ₊pod zvyčajným rádom ≦ nie je ohraničená mriežka, pretože má najmenší prvok 1, ale najväčší prvok neexistuje.

Vlastnosti ohraničených mriežok:

Ak L je ohraničená mriežka, potom pre akýkoľvek prvok a ∈ L máme tieto identity:

a ∨ 1 = 1
a ∧1= a
a ∨0=a
a ∧0=0

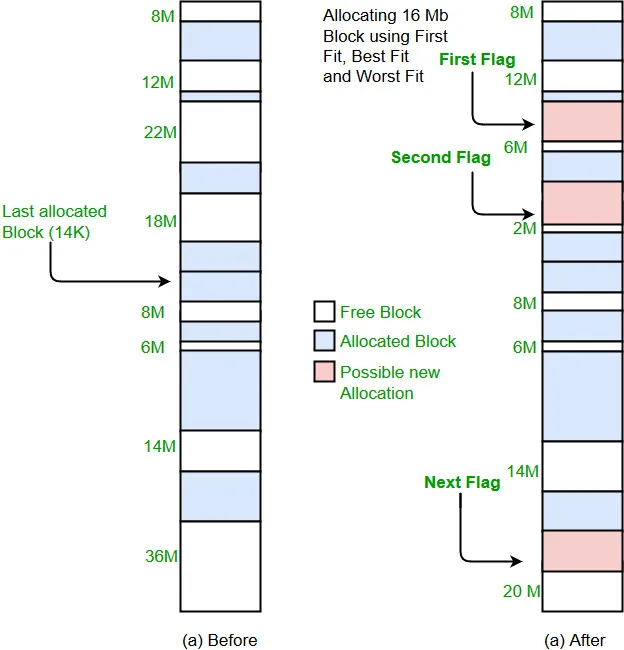
Veta: Dokážte, že každá konečná mriežka L = {a ₁,a ₂,a ₃....a _n} je ohraničený.

dôkaz: Dali sme konečnú mriežku:

L = {a ₁,a ₂,a ₃....a _n}

Najväčším prvkom mriežok L je teda a ₁∨ a ₂∨ a _{3∨.....∨a _n.}

Taktiež najmenší prvok mriežky L je a ₁∧ a ₂∧a ₃∧....∧a _n.

Pretože pre každú konečnú mriežku existujú najväčšie a najmenšie prvky. Preto je L ohraničené.

Podmriežky:

Uvažujme o neprázdnej podmnožine L ₁mriežky L. Potom L ₁sa nazýva podmriežka L, ak L ₁sám je mriežkou, t.j. operácia L, t.j. a ∨ b ∈ L ₁a a ∧ b ∈ L ₁vždy, keď ∈ L ₁a b∈ L ₁.

Príklad: Uvažujme mriežku všetkých +ve celých čísel I ₊pod operáciou deliteľnosti. Mriežka D _nvšetkých deliteľov n > 1 je podmriežkou I ₊.

Určite všetky podmriežky D ₃₀ktoré obsahujú aspoň štyri prvky, D ₃₀={1,2,3,5,6,10,15,30}.

Riešenie: Podmriežky D ₃₀ktoré obsahujú aspoň štyri prvky, sú tieto:

1. {1, 2, 6, 30} 2. {1, 2, 3, 30}
3. {1, 5, 15, 30} 4. {1, 3, 6, 30}
5. {1, 5, 10, 30} 6. {1, 3, 15, 30}
7. {2, 6, 10, 30}

Izomorfné mriežky:

Dve mriežky L ₁a L ₂sa nazývajú izomorfné mriežky, ak existuje bijekcia z L ₁do L ₂t.j. f: L ₁⟶ L ₂tak, že f (a ∧ b) = f(a)∧ f(b) a f (a ∨ b) = f (a) ∨ f (b)

Príklad: Určite, či sú mriežky znázornené na obr izomorfné.

Riešenie: Mriežky zobrazené na obr sú izomorfné. Uvažujme zobrazenie f = {(a, 1), (b, 2), (c, 3), (d, 4)}. Napríklad f (b ∧ c) = f (a) = 1. majú f (b) ∧ f (c) = 2 ∧ 3 = 1

Distribučná mriežka:

Mriežka L sa nazýva distributívna mriežka, ak pre ľubovoľné prvky a, b a c z L spĺňa tieto distribučné vlastnosti:

a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)
a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)

Ak mriežka L nespĺňa vyššie uvedené vlastnosti, nazýva sa nedistributívna mriežka.

Príklad:

Výkonová množina P (S) množiny S pri operácii prieniku a zjednotenia je distributívna funkcia. keďže
a ∩ (b ∪ c) = (a ∩ b) ∪ (a ∩ c)
a tiež a ∪ (b ∩ c) = (a ∪ b) ∩ (a ∪c) pre ľubovoľné množiny a, b a c P(S).
Mriežka znázornená na obr. II je distributívna. Pretože spĺňa distribučné vlastnosti pre všetky objednané trojky, ktoré sú prevzaté z 1, 2, 3 a 4.

Doplnky a doplnené mriežky:

Nech L je ohraničená mriežka s dolnou hranicou o a hornou hranicou I. Nech a je prvok, ak L. Prvok x v L sa nazýva doplnok a, ak a ∨ x = I a a ∧ x = 0

O mriežke L sa hovorí, že je doplnená, ak je L ohraničená a každý prvok v L má doplnok.

Príklad: Určte doplnok a a c na obr.

Riešenie: Doplnkom a je d. Pretože a ∨ d = 1 a a ∧ d = 0

Doplnok c neexistuje. Pretože neexistuje žiadny prvok c taký, že c ∨ c'=1 a c ∧ c'= 0.

Modulárna mriežka:

Mriežka (L, ∧,∨) sa nazýva modulárna mriežka, ak a ∨ (b ∧ c) = (a ∨ b) ∧ c vždy, keď a ≦ c.

Priamy súčin mriežok:

Nechajte (L ₁∨ ₁∧ ₁) a (L ₂∨ ₂∧ ₂) byť dve mriežky. Potom (L, ∧,∨) je priamy súčin mriežok, kde L = L ₁x L ₂v ktorej sú binárne operácie ∨(spojenie) a ∧(stretnutie) na L také, že pre ľubovoľný (a ₁,b ₁) a (a ₂,b ₂) v L.