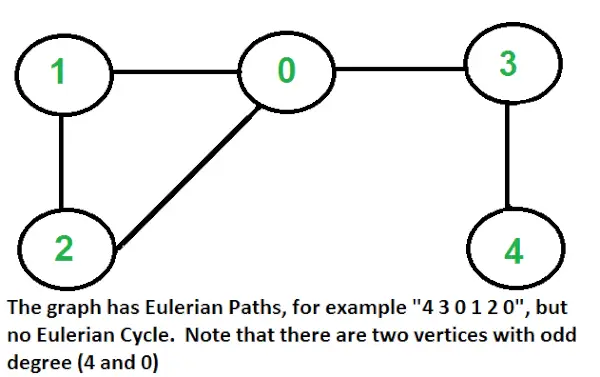
Eulerovská cesta je cesta v grafe, ktorá navštívi každú hranu práve raz. Eulerovský okruh je eulerovská cesta, ktorá začína a končí na rovnakom vrchole.

Ako zistiť, či je daný graf eulerovský alebo nie?

Problém je rovnaký ako v nasledujúcej otázke. Je možné nakresliť daný graf bez toho, aby ste zdvihli ceruzku z papiera a bez toho, aby ste viackrát obkresľovali niektorú z hrán?
Graf sa nazýva eulerovský, ak má eulerovský cyklus, a poloeulerovský, ak má eulerovskú cestu. Zdá sa, že problém je podobný Hamiltonovej ceste, čo je NP úplný problém pre všeobecný graf. Našťastie vieme zistiť, či daný graf má eulerovskú cestu alebo nie v polynomiálnom čase. V skutočnosti ho môžeme nájsť v čase O(V+E).
Nasleduje niekoľko zaujímavých vlastností neorientovaných grafov s eulerovskou dráhou a cyklom. Tieto vlastnosti môžeme použiť na zistenie, či je graf eulerovský alebo nie.

Eulerovský cyklus: Neorientovaný graf má eulerovský cyklus, ak sú splnené dve podmienky.

1. Všetky vrcholy s nenulovým stupňom sú spojené. Nestaráme sa o vrcholy s nulovým stupňom, pretože nepatria do Eulerovského cyklu alebo cesty (berieme do úvahy iba všetky hrany).
2. Všetky vrcholy majú párny stupeň.

Eulerovská cesta: Neorientovaný graf má eulerovskú cestu, ak sú splnené dve podmienky.

1. Rovnaké ako podmienka (a) pre Eulerovský cyklus.
2. Ak nula alebo dva vrcholy majú nepárny stupeň a všetky ostatné vrcholy majú párny stupeň. Všimnite si, že iba jeden vrchol s nepárnym stupňom nie je možný v neorientovanom grafe (súčet všetkých stupňov je vždy párny v neorientovanom grafe)

Všimnite si, že graf bez hrán sa považuje za eulerovský, pretože neexistujú žiadne hrany, ktoré by sa dali prejsť.

Ako to funguje?
V eulerovskej ceste zakaždým, keď navštívime vrchol v, prechádzame cez dve nenavštívené hrany s jedným koncovým bodom ako v. Preto všetky stredné vrcholy v eulerovskej ceste musia mať párny stupeň. Pre Eulerovský cyklus môže byť akýkoľvek vrchol stredným vrcholom, preto musia mať všetky vrcholy párny stupeň.

Odporúčaná prax Eulerov okruh a cesta Vyskúšajte to!

Implementácia:

C++

// A C++ program to check if a given graph is Eulerian or not> #include> #include> using> namespace> std;> // A class that represents an undirected graph> class> Graph> {> > int> V;> // No. of vertices> > list <> int> >*adj;> // A dynamic array of adjacency lists> public> :> > // Constructor and destructor> > Graph(> int> V) {> this> ->V = V; adj => new> list <> int> >[V]; }> > ~Graph() {> delete> [] adj; }> // To avoid memory leak> > // function to add an edge to graph> > void> addEdge(> int> v,> int> w);> > // Method to check if this graph is Eulerian or not> > int> isEulerian();> > // Method to check if all non-zero degree vertices are connected> > bool> isConnected();> > // Function to do DFS starting from v. Used in isConnected();> > void> DFSUtil(> int> v,> bool> visited[]);> };> void> Graph::addEdge(> int> v,> int> w)> {> > adj[v].push_back(w);> > adj[w].push_back(v);> // Note: the graph is undirected> }> void> Graph::DFSUtil(> int> v,> bool> visited[])> {> > // Mark the current node as visited and print it> > visited[v] => true> ;> > // Recur for all the vertices adjacent to this vertex> > list <> int> >::iterátor i;> > for> (i = adj[v].begin(); i != adj[v].end(); ++i)> > if> (!visited[*i])> > DFSUtil(*i, visited);> }> // Method to check if all non-zero degree vertices are connected.> // It mainly does DFS traversal starting from> bool> Graph::isConnected()> {> > // Mark all the vertices as not visited> > bool> visited[V];> > int> i;> > for> (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) návrat false; vrátiť true; } /* Funkcia vráti jednu z nasledujúcich hodnôt 0 --> Ak graf nie je eulerovský 1 --> ak má graf Eulerovu cestu (semieulerovský) 2 --> ak má graf Eulerov obvod (eulerovský) */ int Graph::isEulerian() { // Kontrola, či sú všetky vrcholy nenulového stupňa spojené if (isConnected() == false) return 0; // Počítanie vrcholov s nepárnym stupňom int nepárne = 0; for (int i = 0; i if (adj[i].size() & 1) nepárne++; // Ak je počet väčší ako 2, potom graf nie je eulerovský, ak (nepárne> 2) vráti 0; // Ak je nepárne počet je 2, potom semi-euleriánsky // Ak je nepárny počet 0, potom eulerovský // Všimnite si, že nepárny počet nemôže byť nikdy 1 pre neorientovaný návrat grafu (nepárny) } // Funkcia na spustenie testovacích prípadov test(Graf &g) { int res = g.isEulerian(); if (res == 0) cout < < 'graph is not Eulerian '; else if (res == 1) cout < < 'graph has a Euler path '; else cout < < 'graph has a Euler cycle '; } // Driver program to test above function int main() { // Let us create and test graphs shown in above figures Graph g1(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); test(g1); Graph g2(5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); test(g2); Graph g3(5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); test(g3); // Let us create a graph with 3 vertices // connected in the form of cycle Graph g4(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); test(g4); // Let us create a graph with all vertices // with zero degree Graph g5(3); test(g5); return 0; }>

Java

// A Java program to check if a given graph is Eulerian or not> import> java.io.*;> import> java.util.*;> import> java.util.LinkedList;> // This class represents an undirected graph using adjacency list> // representation> class> Graph> {> > private> int> V;> // No. of vertices> > // Array of lists for Adjacency List Representation> > private> LinkedList adj[];> > // Constructor> > Graph(> int> v)> > {> > V = v;> > adj => new> LinkedList[v];> > for> (> int> i=> 0> ; i adj[i] = new LinkedList(); } //Function to add an edge into the graph void addEdge(int v, int w) { adj[v].add(w);// Add w to v's list. adj[w].add(v); //The graph is undirected } // A function used by DFS void DFSUtil(int v,boolean visited[]) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex Iterator i = adj[v].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from boolean isConnected() { // Mark all the vertices as not visited boolean visited[] = new boolean[V]; int i; for (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) návrat false; vrátiť true; } /* Funkcia vráti jednu z nasledujúcich hodnôt 0 --> Ak graf nie je eulerovský 1 --> ak má graf Eulerovu cestu (semieulerovský) 2 --> ak má graf Eulerov obvod (eulerovský) */ int isEulerian() { // Kontrola, či sú všetky vrcholy nenulového stupňa spojené, ak (isConnected() == false) return 0; // Počítanie vrcholov s nepárnym stupňom int nepárne = 0; for (int i = 0; i if (adj[i].size()%2!=0) nepárne++; // Ak je počet väčší ako 2, potom graf nie je eulerovský, ak (nepárne> 2) vráti 0; / / Ak je nepárny počet 2, potom poloeulerovský // Ak je nepárny počet 0, potom eulerovský // Všimnite si, že nepárny počet nemôže byť nikdy 1 pre neorientovaný návrat grafu (nepárny==2) } //; Funkcia na spustenie testovacích prípadov void test() { int res = isEulerian() if (res == 0) System.out.println('graf nie je eulerovský' else if (res == 1) Systém. out.println('graf má Eulerovu cestu' else System.out.println('graf má Eulerov cyklus' } // Metóda ovládača public static void main(String args[]) { /); / Vytvorme a otestujme grafy uvedené na obrázkoch Graph g1 = new Graph(5); g1.addEdge(0, 2); (0, 3). g1.test(); g2.pridaj(1, 2); pridajHranu(2, 1); g2.pridajHranu(3, 4); g2.test(5); .addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // Vytvorme graf s 3 vrcholmi // spojenými v tvare cyklu Graph g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // Vytvorme graf so všetkými vrcholmi // s nulovým stupňom Graph g5 = new Graph(3); g5.test(); } } // Tento kód prispel Aakash Hasija>

Python3

# Python program to check if a given graph is Eulerian or not> #Complexity : O(V+E)> from> collections> import> defaultdict> # This class represents a undirected graph using adjacency list representation> class> Graph:> > def> __init__(> self> , vertices):> > self> .V> => vertices> # No. of vertices> > self> .graph> => defaultdict(> list> )> # default dictionary to store graph> > # function to add an edge to graph> > def> addEdge(> self> , u, v):> > self> .graph[u].append(v)> > self> .graph[v].append(u)> > # A function used by isConnected> > def> DFSUtil(> self> , v, visited):> > # Mark the current node as visited> > visited[v]> => True> > # Recur for all the vertices adjacent to this vertex> > for> i> in> self> .graph[v]:> > if> visited[i]> => => False> :> > self> .DFSUtil(i, visited)> > '''Method to check if all non-zero degree vertices are> > connected. It mainly does DFS traversal starting from> > node with non-zero degree'''> > def> isConnected(> self> ):> > # Mark all the vertices as not visited> > visited> => [> False> ]> *> (> self> .V)> > # Find a vertex with non-zero degree> > for> i> in> range> (> self> .V):> > if> len> (> self> .graph[i]) !> => 0> :> > break> > # If there are no edges in the graph, return true> > if> i> => => self> .V> -> 1> :> > return> True> > # Start DFS traversal from a vertex with non-zero degree> > self> .DFSUtil(i, visited)> > # Check if all non-zero degree vertices are visited> > for> i> in> range> (> self> .V):> > if> visited[i]> => => False> and> len> (> self> .graph[i])>> 0> :> > return> False> > return> True> > '''The function returns one of the following values> > 0 -->Ak graf nie je eulerovský> > 1 -->Ak má graf Eulerovu cestu (semi-eulerovská)> > 2 -->Ak má graf Eulerov obvod (eulerovský) '''> > def> isEulerian(> self> ):> > # Check if all non-zero degree vertices are connected> > if> self> .isConnected()> => => False> :> > return> 0> > else> :> > # Count vertices with odd degree> > odd> => 0> > for> i> in> range> (> self> .V):> > if> len> (> self> .graph[i])> %> 2> !> => 0> :> > odd> +> => 1> > '''If odd count is 2, then semi-eulerian.> > If odd count is 0, then eulerian> > If count is more than 2, then graph is not Eulerian> > Note that odd count can never be 1 for undirected graph'''> > if> odd> => => 0> :> > return> 2> > elif> odd> => => 2> :> > return> 1> > elif> odd>> 2> :> > return> 0> > # Function to run test cases> > def> test(> self> ):> > res> => self> .isEulerian()> > if> res> => => 0> :> > print> (> 'graph is not Eulerian'> )> > elif> res> => => 1> :> > print> (> 'graph has a Euler path'> )> > else> :> > print> (> 'graph has a Euler cycle'> )> # Let us create and test graphs shown in above figures> g1> => Graph(> 5> )> g1.addEdge(> 1> ,> 0> )> g1.addEdge(> 0> ,> 2> )> g1.addEdge(> 2> ,> 1> )> g1.addEdge(> 0> ,> 3> )> g1.addEdge(> 3> ,> 4> )> g1.test()> g2> => Graph(> 5> )> g2.addEdge(> 1> ,> 0> )> g2.addEdge(> 0> ,> 2> )> g2.addEdge(> 2> ,> 1> )> g2.addEdge(> 0> ,> 3> )> g2.addEdge(> 3> ,> 4> )> g2.addEdge(> 4> ,> 0> )> g2.test()> g3> => Graph(> 5> )> g3.addEdge(> 1> ,> 0> )> g3.addEdge(> 0> ,> 2> )> g3.addEdge(> 2> ,> 1> )> g3.addEdge(> 0> ,> 3> )> g3.addEdge(> 3> ,> 4> )> g3.addEdge(> 1> ,> 3> )> g3.test()> # Let us create a graph with 3 vertices> # connected in the form of cycle> g4> => Graph(> 3> )> g4.addEdge(> 0> ,> 1> )> g4.addEdge(> 1> ,> 2> )> g4.addEdge(> 2> ,> 0> )> g4.test()> # Let us create a graph with all vertices> # with zero degree> g5> => Graph(> 3> )> g5.test()> # This code is contributed by Neelam Yadav>

C#

// A C# program to check if a given graph is Eulerian or not> using> System;> using> System.Collections.Generic;> > // This class represents an undirected graph using adjacency list> // representation> public> class> Graph> {> > private> int> V;> // No. of vertices> > > // Array of lists for Adjacency List Representation> > private> List <> int> >[]adj;> > > // Constructor> > Graph(> int> v)> > {> > V = v;> > adj => new> List <> int> >[v];> > for> (> int> i=0; i adj[i] = new List (); } //Funkcia na pridanie hrany do grafu void addEdge(int v, int w) { adj[v].Add(w);// Pridať w do zoznamu v. adj[w].Add(v); //Graf je neorientovaný } // Funkcia používaná DFS void DFSUtil(int v,bool []navštívené) { // Označenie aktuálneho uzla ako navštívené[v] = true; // Opakuje sa pre všetky vrcholy susediace s týmto vrcholom foreach(int i in adj[v]){ int n = i; if (!navštívené[n]) DFSUtil(n, navštívené); } } // Metóda na kontrolu, či sú // všetky vrcholy nenulového stupňa spojené. Vykonáva hlavne prechod DFS od bool isConnected() { // Označí všetky vrcholy ako nenavštívené bool []navštívené = new bool[V]; int i; for (i = 0; navštívil som[i] = nepravda; // Nájdite vrchol s nenulovým stupňom pre (i = 0; i if (adj[i].Count != 0) break); // Ak existujú žiadne hrany v grafe, return true if (i == V) return true // Spustenie DFS prechodu z vrcholu s nenulovým stupňom DFSUtil(i, navštívené); for (i = 0; i if (navštívené[i] == false && adj[i].Count> 0) return false; return true; } /* Funkcia vráti jednu z nasledujúcich hodnôt 0 --> Ak je graf nie je Eulerovský 1 --> Ak má graf Eulerovu cestu (semi-eulerovský) 2 --> Ak má graf Eulerov obvod (eulerovský) */ int isEulerian() { // Skontrolujte, či sú všetky vrcholy nenulového stupňa spojené, ak (isConnected() == false) return 0 // Spočítajte vrcholy s nepárnym stupňom int nepárne = 0; počet je viac ako 2, potom graf nie je eulerovský, ak (nepárne> 2) vráti 0 // Ak je nepárny počet 2, potom je poloeulerovský // Ak je nepárny počet 0, potom je eulerovský // Všimnite si, že nepárny počet môže nikdy nebude 1 pre nepriamy návrat grafu (nepárne==2)? 1 : 2; } // Funkcia na spustenie testovacích prípadov void test() { int res = isEulerian(); if (res == 0) Console.WriteLine('graf nie je eulerovský'); else if (res == 1) Console.WriteLine('graf má Eulerovu cestu'); else Console.WriteLine('graf má Eulerov cyklus'); } // Metóda ovládača public static void Main(String []args) { // Vytvorme a otestujme grafy zobrazené na obrázkoch vyššie Graph g1 = new Graph(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); g1.test(); Graph g2 = new Graph(5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); g2.test(); Graph g3 = new Graph(5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // Vytvorme graf s 3 vrcholmi // spojenými v tvare cyklu Graph g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // Vytvorme graf so všetkými vrcholmi // s nulovým stupňom Graph g5 = new Graph(3); g5.test(); } } // Tento kód prispel PrinceRaj1992>

Javascript

> // A Javascript program to check if a given graph is Eulerian or not> // This class represents an undirected graph using adjacency list> // representation> class Graph> {> > // Constructor> > constructor(v)> > {> > this> .V = v;> > this> .adj => new> Array(v);> > for> (let i = 0; i this.adj[i] = []; } // Function to add an edge into the graph addEdge(v,w) { this.adj[v].push(w);// Add w to v's list. this.adj[w].push(v); //The graph is undirected } // A function used by DFS DFSUtil(v,visited) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex for(let i of this.adj[v]) { let n = i; if (!visited[n]) this.DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from isConnected() { // Mark all the vertices as not visited let visited = new Array(this.V); let i; for (i = 0; i 0) návrat false; vrátiť true; } /* Funkcia vráti jednu z nasledujúcich hodnôt 0 --> Ak graf nie je eulerovský 1 --> ak má graf Eulerovu cestu (semieulerovský) 2 --> ak má graf Eulerov obvod (eulerovský) */ isEulerian() { // Skontrolujte, či sú všetky vrcholy s nenulovým stupňom spojené, ak (this.isConnected() == false) return 0; // Spočítajte vrcholy s nepárnym stupňom nech nepárny = 0; pre (nech i = 0; i 2) návrat 0; // Ak je nepárny počet 2, potom poloeulerovský. // Ak je nepárny počet 0, potom je eulerovský // Všimnite si, že nepárny počet nemôže byť nikdy 1 pre neorientovaný návrat grafu (nepárny==2)? 1 : 2; } // Funkcia na spustenie testovacích prípadov test() { nech res = this.isEulerian(); if (res == 0) document.write('graf nie je eulerovský '); else if (res == 1) document.write('graf má Eulerovu cestu '); else document.write('graf má Eulerov cyklus '); } } // Metóda ovládača // Vytvorme a otestujme grafy zobrazené na obrázkoch vyššie nech g1 = new Graph(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); g1.test(); nech g2 = new Graph(5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); g2.test(); nech g3 = new Graph(5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // Vytvorme graf s 3 vrcholmi // spojenými v tvare cyklu nech g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // Vytvorme graf so všetkými vrcholmi // s nulovým stupňom nech g5 = new Graph(3); g5.test(); // Tento kód prispel avanitrachhadiya2155>

Výkon

graph has a Euler path graph has a Euler cycle graph is not Eulerian graph has a Euler cycle graph has a Euler cycle 

Časová zložitosť: O(V+E)

Priestorová zložitosť: O(V+E)

Ďalšie články:
Eulerovská cesta a okruh pre riadené grafy.
Fleuryho algoritmus na tlač eulerovskej cesty alebo okruhu?