Skontrolujte, či bod v kruhovom sektore existuje alebo nie.
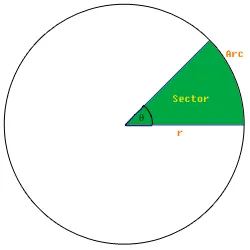
Máme kruh so stredom na začiatku (0 0). Ako vstup je uvedený počiatočný uhol kruhového sektora a veľkosť kruhového sektora v percentách.
Príklady:
Input : Radius = 8 StartAngle = 0 Percentage = 12 x = 3 y = 4 Output : Point (3 4) exists in the circle sector Input : Radius = 12 Startangle = 45 Percentage = 25 x = 3 y = 4 Output : Point (3 4) does not exist in the circle sector
 Zdroj: Wikibook.org
Zdroj: Wikibook.org
Na tomto obrázku je počiatočný uhol 0 stupňov polomer r a predpokladajme, že percento farebnej plochy je 12 %, potom vypočítame koncový uhol ako 360/percento + počiatočný uhol .
Aby sme zistili, či bod (x y) existuje v kruhovom sektore (so stredom v počiatku) alebo nie, nájdeme polárne súradnice tohto bodu a potom prejdeme nasledujúcimi krokmi:
- Pomocou toho preveďte x y na polárne súradnice
Uhol = absencia (y/x); Polomer = sqrt(x * y y y y y y); - Potom musí byť Uhol medzi počiatočným uhlom a koncovým uhlom a polomer medzi 0 a vaším polomerom.
// C++ program to check if a point lies inside a circle // sector. #include using namespace std ; void checkPoint ( int radius int x int y float percent float startAngle ) { // calculate endAngle float endAngle = 360 / percent + startAngle ; // Calculate polar co-ordinates float polarradius = sqrt ( x * x + y * y ); float Angle = atan ( y / x ); // Check whether polarradius is less then radius of circle // or not and Angle is between startAngle and endAngle // or not if ( Angle >= startAngle && Angle <= endAngle && polarradius < radius ) printf ( 'Point (%d %d) exist in the circle sector n ' x y ); else printf ( 'Point (%d %d) does not exist in the circle sector n ' x y ); } // Driver code int main () { int radius = 8 x = 3 y = 4 ; float percent = 12 startAngle = 0 ; checkPoint ( radius x y percent startAngle ); return 0 ; }
Java // Java program to check if // a point lies inside a circle // sector. class GFG { static void checkPoint ( int radius int x int y float percent float startAngle ) { // calculate endAngle float endAngle = 360 / percent + startAngle ; // Calculate polar co-ordinates double polarradius = Math . sqrt ( x * x + y * y ); double Angle = Math . atan ( y / x ); // Check whether polarradius is // less then radius of circle // or not and Angle is between // startAngle and endAngle // or not if ( Angle >= startAngle && Angle <= endAngle && polarradius < radius ) System . out . print ( 'Point' + '(' + x + '' + y + ')' + ' exist in the circle sectorn' ); else System . out . print ( 'Point' + '(' + x + '' + y + ')' + ' exist in the circle sectorn' ); } // Driver Program to test above function public static void main ( String arg [] ) { int radius = 8 x = 3 y = 4 ; float percent = 12 startAngle = 0 ; checkPoint ( radius x y percent startAngle ); } } // This code is contributed // by Anant Agarwal.
Python3 # Python3 program to check if a point # lies inside a circle sector. import math def checkPoint ( radius x y percent startAngle ): # calculate endAngle endAngle = 360 / percent + startAngle # Calculate polar co-ordinates polarradius = math . sqrt ( x * x + y * y ) Angle = math . atan ( y / x ) # Check whether polarradius is less # then radius of circle or not and # Angle is between startAngle and # endAngle or not if ( Angle >= startAngle and Angle <= endAngle and polarradius < radius ): print ( 'Point (' x '' y ') ' 'exist in the circle sector' ) else : print ( 'Point (' x '' y ') ' 'does not exist in the circle sector' ) # Driver code radius x y = 8 3 4 percent startAngle = 12 0 checkPoint ( radius x y percent startAngle ) # This code is contributed by # Smitha Dinesh Semwal
C# // C# program to check if a point lies // inside a circle sector. using System.IO ; using System ; class GFG { static void checkPoint ( int radius int x int y float percent float startAngle ) { // calculate endAngle float endAngle = 360 / percent + startAngle ; // Calculate polar co-ordinates float polarradius = ( float ) Math . Sqrt ( x * x + y * y ); float Angle = ( float ) Math . Atan ( y / x ); // Check whether polarradius is less then // radius of circle or not and Angle is // between startAngle and endAngle or not if ( Angle >= startAngle && Angle <= endAngle && polarradius < radius ) Console . Write ( 'Point ({0} {1}) exist in ' + 'the circle sector' x y ); else Console . Write ( 'Point ({0} {1}) does not ' + 'exist in the circle sector' x y ); } // Driver code public static void Main () { int radius = 8 x = 3 y = 4 ; float percent = 12 startAngle = 0 ; checkPoint ( radius x y percent startAngle ); } } // This code is contributed by Smitha Dinesh Semwal
JavaScript < script > // Javascript program to check if // a point lies inside a circle // sector. function checkPoint ( radius x y percent startAngle ) { // Calculate endAngle let endAngle = 360 / percent + startAngle ; // Calculate polar co-ordinates let polarradius = Math . sqrt ( x * x + y * y ); let Angle = Math . atan ( y / x ); // Check whether polarradius is // less then radius of circle // or not and Angle is between // startAngle and endAngle // or not if ( Angle >= startAngle && Angle <= endAngle && polarradius < radius ) document . write ( 'Point' + '(' + x + '' + y + ')' + ' exist in the circle sectorn' ); else document . write ( 'Point' + '(' + x + '' + y + ')' + ' exist in the circle sectorn' ); } // Driver code let radius = 8 x = 3 y = 4 ; let percent = 12 startAngle = 0 ; checkPoint ( radius x y percent startAngle ); // This code is contributed by splevel62 < /script>
výstup:
Point(3 4) exists in the circle sector
Časová zložitosť: O(1)
Pomocný priestor: O(1)