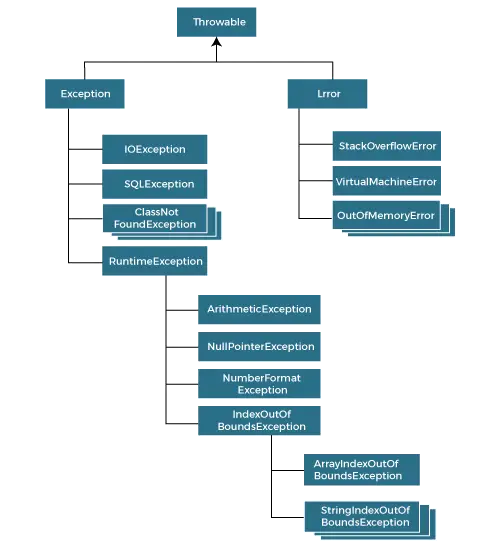
ANALÝZA ALGORITMOV | VEĽKÝ - Θ (BIG THETA) ZÁPIS - TECHCODEVIEW.COM

V analýza algoritmov asymptotické zápisy sa používajú na vyhodnotenie výkonu algoritmu v jeho najlepšie prípady a najhoršie prípady . Tento článok sa bude zaoberať notáciami Big – Theta reprezentovanými gréckym písmenom (Θ).

Definícia: Nech g a f je funkcia z množiny prirodzených čísel pre seba. O funkcii f hovoríme, že je Θ(g), ak existujú konštanty c ₁ , c ₂ > 0 a prirodzené číslo n ₀ také, že c ₁ * g(n) ≤ f(n) ≤ c ₂ * g(n) pre všetky n ≥ n ₀

Matematické znázornenie:

Θ (g(n)) = {f(n): existujú kladné konštanty c ₁ , c ₂ a n ₀ tak, že 0 ≤ c ₁ * g(n) ≤ f(n) ≤ c ₂ * g(n) pre všetky n ≥ n ₀ }
Poznámka: Θ(g) je množina

Vyššie uvedená definícia znamená, že ak f(n) je theta g(n), potom hodnota f(n) je vždy medzi c1 * g(n) a c2 * g(n) pre veľké hodnoty n (n ≥ n ₀ ). Definícia theta tiež vyžaduje, aby f(n) bolo nezáporné pre hodnoty n väčšie ako n ₀ .

Grafické znázornenie:

Grafické znázornenie

V jednoduchom jazyku, Big – Theta (Θ) zápis špecifikuje asymptotické hranice (horné aj dolné) pre funkciu f(n) a poskytuje priemernú časovú zložitosť algoritmu.

Ak chcete zistiť priemernú časovú zložitosť akéhokoľvek programu, postupujte podľa nasledujúcich krokov:

Rozdeľte program na menšie časti.
Nájdite všetky typy a počet vstupov a vypočítajte počet operácií, ktoré je potrebné vykonať. Uistite sa, že vstupné prípady sú rovnomerne rozdelené.
Nájdite súčet všetkých vypočítaných hodnôt a vydeľte súčet celkovým počtom vstupov, povedzme, že získaná funkcia n je g(n) po odstránení všetkých konštánt, potom v notácii Θ je reprezentovaná ako Θ(g(n))

Príklad: Zvážte príklad pomocou lineárneho vyhľadávania zistite, či kľúč v poli existuje alebo nie . Myšlienka je prejsť po poli a skontrolujte každý prvok, či sa rovná kľúču alebo nie.

Pseudokód je nasledovný:

bool linearSearch(int a[], int n, int key) {  for (int i = 0; i   if (a[i] == key)  return true;  }   return false; }

Nižšie je uvedená implementácia vyššie uvedeného prístupu:

C++

// C++ program for the above approach> #include> using> namespace> std;> // Function to find whether a key exists in an> // array or not using linear search> bool> linearSearch(> int> a[],> int> n,> int> key)> {> > // Traverse the given array, a[]> > for> (> int>

i = 0; i   // Check if a[i] is equal to key  if (a[i] == key)  return true;  }  return false; } // Driver Code int main() {  // Given Input  int arr[] = { 2, 3, 4, 10, 40 };  int x = 10;  int n = sizeof(arr) / sizeof(arr[0]);  // Function Call    if (linearSearch(arr, n, x))  cout  < < 'Element is present in array';  else  cout  < < 'Element is not present in array';  return 0; }>

Java

// Java program for the above approach> import> java.lang.*;> import> java.util.*;> class> GFG{> // Function to find whether a key exists in an> // array or not using linear search> static> boolean> linearSearch(> int> a[],> int> n,> > int> key)> {> > > // Traverse the given array, a[]> > for> (> int> i => 0>

; i   {    // Check if a[i] is equal to key  if (a[i] == key)  return true;  }  return false; } // Driver code public static void main(String[] args) {    // Given Input  int arr[] = { 2, 3, 4, 10, 40 };  int x = 10;  int n = arr.length;  // Function Call  if (linearSearch(arr, n, x))  System.out.println('Element is present in array');  else  System.out.println('Element is not present in array'); } } // This code is contributed by avijitmondal1998>

Python3

# Python3 program for the above approach> # Function to find whether a key exists in an> # array or not using linear search> def> linearSearch(a, n, key):> > # Traverse the given array, a[]> > for> i> in> range> (> 0> , n):> > # Check if a[i] is equal to key> > if> (a[i]> => => key):> > return> True> > > return> False> # Driver Code> # Given Input> arr> => 2> ,> 3> ,> 4> ,> 10> ,> 40> x> => 10> n> => len> (arr)> # Function Call> if> (linearSearch(arr, n, x)):> > print> (> 'Element is present in array'> )> else> :> > print> (> 'Element is not present in array'> )> > # This code is contributed by shivanisinghss2110>

C#

// C# program for above approach> using> System;> class> GFG{> // Function to find whether a key exists in an> // array or not using linear search> static> bool> linearSearch(> int> [] a,> int> n,> > int> key)> {> > > // Traverse the given array, a[]> > for> (> int>

i = 0; i   {    // Check if a[i] is equal to key  if (a[i] == key)  return true;  }  return false; } // Driver Code static void Main() {  // Given Input  int[] arr = { 2, 3, 4, 10, 40 };  int x = 10;  int n = arr.Length;  // Function Call  if (linearSearch(arr, n, x))  Console.Write('Element is present in array');  else  Console.Write('Element is not present in array'); } } // This code is contributed by sanjoy_62.>

Javascript

> // JavaScript program for the above approach> // Function to find whether a key exists in an> // array or not using linear search> function> linearSearch(a, n, key)> {> > > // Traverse the given array, a[]> > for> (> var>

i = 0; i   {    // Check if a[i] is equal to key  if (a[i] == key)  return true;  }  return false; } // Driver code  // Given Input  var arr = [ 2, 3, 4, 10, 40 ];  var x = 10;  var n = arr.length;  // Function Call  if (linearSearch(arr, n, x))  document.write('Element is present in array');  else  document.write('Element is not present in array'); // This code is contributed by shivanisinghss2110>

Výkon

Element is present in array

Časová zložitosť: O(n)
Pomocný priestor: O(1)

Pri lineárnom vyhľadávacom probléme predpokladajme, že sú to všetky prípady rovnomerne rozložené (vrátane prípadu, keď kľúč v poli chýba). Takže spočítajte všetky prípady (keď je kľúč prítomný na pozícii 1, 2, 3, ……, n a nie je prítomný, a vydeľte súčet n + 1.

Priemerná časová zložitosť prípadu = $frac{sum_{i=1}^{n+1} heta(i)}{n + 1}$

⇒ $frac{ heta((n+1)*(n+2)/2)}{n+1}$

⇒

⇒ (konštanty sú odstránené)

Kedy použiť veľký – Θ zápis: Big – Θ analyzuje algoritmus s najpresnejšou presnosťou, pretože pri výpočte Big – Θ sa berie do úvahy rovnomerné rozdelenie rôzneho typu a dĺžky vstupov, poskytuje priemernú časovú zložitosť algoritmu, ktorá je pri analýze najpresnejšia, ale v praxi niekedy je ťažké nájsť rovnomerne rozloženú množinu vstupov pre algoritmus, v tom prípade, Big-O zápis sa používa, ktorý predstavuje asymptotickú hornú hranicu funkcie f.

Ďalšie podrobnosti nájdete na stránke: Návrh a analýza algoritmov .