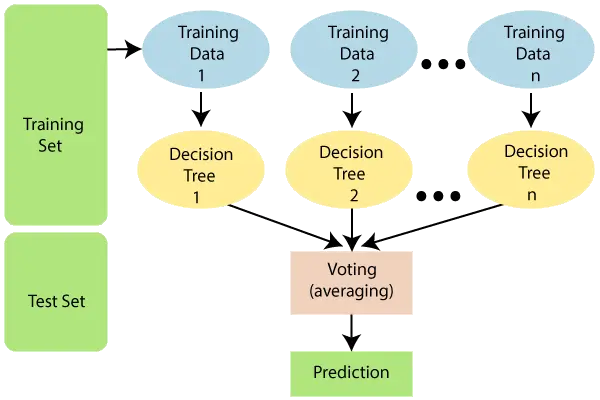
Acoperirea totală a tuturor zerourilor într-o matrice binară

 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; } Având în vedere o matrice binară, care conține doar 0 și 1, trebuie să găsim suma acoperirii tuturor zerourilor matricei, unde acoperirea pentru un anumit 0 este definită ca numărul total de unități în jurul unui zero în direcțiile stânga-dreapta sus și jos. Acestea pot fi oriunde până la un colț într-o direcție.
Exemple:
Input : mat[][] = {0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0} Output : 20 First four zeros are surrounded by only one 1. So coverage for zeros in first row is 1 + 1 + 1 + 1 Zeros in second row are surrounded by three 1's. Note that there is no 1 above. There are 1's in all other three directions. Coverage of zeros in second row = 3 + 3. Similarly counting for others also we get overall count as below. 1 + 1 + 1 + 1 + 3 + 3 + 2 + 2 + 2 + 2 + 2 = 20 Input : mat[][] = {1 1 1 0 1 0 0 1} Output : 8 Coverage of first zero is 2 Coverages of other two zeros is 3 Total coverage = 2 + 3 + 3 = 8 Recommended Practice Acoperirea tuturor zerourilor într-o matrice binară Încearcă! O solutie simpla Pentru a rezolva această problemă, este numărarea celor în jurul zerourilor în mod independent, adică rulăm bucla de patru ori în fiecare direcție pentru fiecare celulă pentru matricea dată. Ori de câte ori găsim un 1 în orice buclă, întrerupem bucla și creștem rezultatul cu 1.
Un solutie eficienta este să faci următoarele.
- Parcurgeți toate rândurile de la stânga la dreapta rezultatul creșterii dacă un 1 este deja văzut (în traversarea curentă) și elementul curent este 0.
- Parcurgeți toate rândurile de la dreapta la stânga rezultatul incrementarii dacă un 1 este deja văzut (în traversarea curentă) și elementul curent este 0.
- Parcurgeți toate coloanele de sus în jos rezultatul creșterii dacă un 1 este deja văzut (în traversarea curentă) și elementul curent este 0.
- Parcurgeți toate coloanele de jos în sus, rezultatul creșterii dacă un 1 este deja văzut (în traversarea curentă) și elementul curent este 0.
În codul de mai jos este luată o variabilă booleană isOne, care devine adevărată de îndată ce se întâlnește una în traversarea curentă pentru toate zerourile, după ce rezultatul iterației este incrementat printr-o procedură aplicată în toate cele patru direcții pentru a obține răspunsul final. Resetăm isOne la false după fiecare traversare.
C++ // C++ program to get total coverage of all zeros in // a binary matrix #include using namespace std ; #define R 4 #define C 4 // Returns total coverage of all zeros in mat[][] int getTotalCoverageOfMatrix ( int mat [ R ][ C ]) { int res = 0 ; // looping for all rows of matrix for ( int i = 0 ; i < R ; i ++ ) { bool isOne = false ; // 1 is not seen yet // looping in columns from left to right // direction to get left ones for ( int j = 0 ; j < C ; j ++ ) { // If one is found from left if ( mat [ i ][ j ] == 1 ) isOne = true ; // If 0 is found and we have found // a 1 before. else if ( isOne ) res ++ ; } // Repeat the above process for right to // left direction. isOne = false ; for ( int j = C -1 ; j >= 0 ; j -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns for up and down // directions. for ( int j = 0 ; j < C ; j ++ ) { bool isOne = false ; // 1 is not seen yet for ( int i = 0 ; i < R ; i ++ ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( int i = R -1 ; i >= 0 ; i -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } // Driver code to test above methods int main () { int mat [ R ][ C ] = {{ 0 0 0 0 } { 1 0 0 1 } { 0 1 1 0 } { 0 1 0 0 } }; cout < < getTotalCoverageOfMatrix ( mat ); return 0 ; }
Java // Java program to get total // coverage of all zeros in // a binary matrix import java . io . * ; class GFG { static int R = 4 ; static int C = 4 ; // Returns total coverage // of all zeros in mat[][] static int getTotalCoverageOfMatrix ( int [][] mat ) { int res = 0 ; // looping for all // rows of matrix for ( int i = 0 ; i < R ; i ++ ) { // 1 is not seen yet boolean isOne = false ; // looping in columns from // left to right direction // to get left ones for ( int j = 0 ; j < C ; j ++ ) { // If one is found // from left if ( mat [ i ][ j ] == 1 ) isOne = true ; // If 0 is found and we // have found a 1 before. else if ( isOne ) res ++ ; } // Repeat the above // process for right // to left direction. isOne = false ; for ( int j = C - 1 ; j >= 0 ; j -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns // for up and down directions. for ( int j = 0 ; j < C ; j ++ ) { // 1 is not seen yet boolean isOne = false ; for ( int i = 0 ; i < R ; i ++ ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( int i = R - 1 ; i >= 0 ; i -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } // Driver code static public void main ( String [] args ) { int [][] mat = {{ 0 0 0 0 } { 1 0 0 1 } { 0 1 1 0 } { 0 1 0 0 }}; System . out . println ( getTotalCoverageOfMatrix ( mat )); } } // This code is contributed by anuj_67.
Python3 # Python3 program to get total coverage of all zeros in # a binary matrix R = 4 C = 4 # Returns total coverage of all zeros in mat[][] def getTotalCoverageOfMatrix ( mat ): res = 0 # looping for all rows of matrix for i in range ( R ): isOne = False # 1 is not seen yet # looping in columns from left to right # direction to get left ones for j in range ( C ): # If one is found from left if ( mat [ i ][ j ] == 1 ): isOne = True # If 0 is found and we have found # a 1 before. else if ( isOne ): res += 1 # Repeat the above process for right to # left direction. isOne = False for j in range ( C - 1 - 1 - 1 ): if ( mat [ i ][ j ] == 1 ): isOne = True else if ( isOne ): res += 1 # Traversing across columns for up and down # directions. for j in range ( C ): isOne = False # 1 is not seen yet for i in range ( R ): if ( mat [ i ][ j ] == 1 ): isOne = True else if ( isOne ): res += 1 isOne = False for i in range ( R - 1 - 1 - 1 ): if ( mat [ i ][ j ] == 1 ): isOne = True else if ( isOne ): res += 1 return res # Driver code mat = [[ 0 0 0 0 ][ 1 0 0 1 ][ 0 1 1 0 ][ 0 1 0 0 ]] print ( getTotalCoverageOfMatrix ( mat )) # This code is contributed by shubhamsingh10
C# // C# program to get total coverage // of all zeros in a binary matrix using System ; class GFG { static int R = 4 ; static int C = 4 ; // Returns total coverage of all zeros in mat[][] static int getTotalCoverageOfMatrix ( int [] mat ) { int res = 0 ; // looping for all rows of matrix for ( int i = 0 ; i < R ; i ++ ) { // 1 is not seen yet bool isOne = false ; // looping in columns from left to // right direction to get left ones for ( int j = 0 ; j < C ; j ++ ) { // If one is found from left if ( mat [ i j ] == 1 ) isOne = true ; // If 0 is found and we // have found a 1 before. else if ( isOne ) res ++ ; } // Repeat the above process for // right to left direction. isOne = false ; for ( int j = C - 1 ; j >= 0 ; j -- ) { if ( mat [ i j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns // for up and down directions. for ( int j = 0 ; j < C ; j ++ ) { // 1 is not seen yet bool isOne = false ; for ( int i = 0 ; i < R ; i ++ ) { if ( mat [ i j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( int i = R - 1 ; i >= 0 ; i -- ) { if ( mat [ i j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } // Driver code to test above methods static public void Main () { int [] mat = {{ 0 0 0 0 } { 1 0 0 1 } { 0 1 1 0 } { 0 1 0 0 }}; Console . WriteLine ( getTotalCoverageOfMatrix ( mat )); } } // This code is contributed by vt_m.
JavaScript < script > // Javascript program to get total // coverage of all zeros in // a binary matrix let R = 4 ; let C = 4 ; // Returns total coverage // of all zeros in mat[][] function getTotalCoverageOfMatrix ( mat ) { let res = 0 ; // looping for all // rows of matrix for ( let i = 0 ; i < R ; i ++ ) { // 1 is not seen yet let isOne = false ; // looping in columns from // left to right direction // to get left ones for ( let j = 0 ; j < C ; j ++ ) { // If one is found // from left if ( mat [ i ][ j ] == 1 ) isOne = true ; // If 0 is found and we // have found a 1 before. else if ( isOne ) res ++ ; } // Repeat the above // process for right // to left direction. isOne = false ; for ( let j = C - 1 ; j >= 0 ; j -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns // for up and down directions. for ( let j = 0 ; j < C ; j ++ ) { // 1 is not seen yet let isOne = false ; for ( let i = 0 ; i < R ; i ++ ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( let i = R - 1 ; i >= 0 ; i -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } let mat = [[ 0 0 0 0 ] [ 1 0 0 1 ] [ 0 1 1 0 ] [ 0 1 0 0 ]]; document . write ( getTotalCoverageOfMatrix ( mat )); < /script>
Ieșire
20
Complexitatea timpului: O(n 2 )
Spațiu auxiliar: O(1)
Creați un test