Componente puternic conectate (SCC) sunt un concept fundamental în teoria grafurilor și algoritmi. Într-un grafic direcționat, a Componentă puternic conectată este un subset de vârfuri în care fiecare vârf din submulțime este accesibil de la orice alt vârf din aceeași submulțime prin parcurgerea muchiilor direcționate. Găsirea SCC-uri a unui grafic poate oferi perspective importante asupra structurii și conectivității graficului, cu aplicații în diverse domenii, cum ar fi analiza rețelelor sociale, accesarea cu crawlere web și rutarea rețelei . Acest tutorial va explora definiția, proprietățile și algoritmii eficienți pentru identificarea componentelor puternic conectate în structurile de date grafice

Cuprins

• Ce este Componentele Strongly Connected (SCC)?
• De ce sunt importante componentele puternic conectate (SCC)?
• Diferența dintre componentele conectate și cele puternic conectate (SCC)
• De ce metoda DFS convențională nu poate fi folosită pentru a găsi componente puternic conectate?
• Conectarea a două componente puternic conectate printr-o margine unidirecțională
• Abordarea forței brute pentru găsirea de componente puternic conectate
• Abordare eficientă pentru găsirea de componente puternic conectate (SCC)
• 1. Algoritmul lui Kosaraju:
• 2. Algoritmul lui Tarjan:
• Concluzie

Ce este Componentele Strongly Connected (SCC)?

A componentă puternic conectată a unui graf direcționat este un subgraf maxim în care fiecare pereche de vârfuri este reciproc accesibilă. Aceasta înseamnă că pentru oricare două noduri A și B din acest subgraf, există o cale de la A la B și o cale de la B la A.

De exemplu: Graficul de mai jos are două componente puternic conectate {1,2,3,4} și {5,6,7}, deoarece există o cale de la fiecare vârf la fiecare alt vârf în aceeași componentă puternic conectată.

Componentă puternic conectată

De ce sunt importante componentele puternic conectate (SCC)?

Înțelegerea SCC-urilor este crucială pentru diverse aplicații, cum ar fi:

• Analiza rețelei : Identificarea clusterelor de noduri strâns interconectate.
• Optimizarea crawlerelor web : determinarea unor părți ale graficului web care sunt strâns legate.
• Rezolvarea dependenței : În software, înțelegerea care module sunt interdependente.

Diferența dintre componentele conectate și cele puternic conectate ( SCC)

Conectivitate în a grafic nedirecţionat se referă la dacă două vârfuri sunt accesibile unul de celălalt sau nu. Se spune că două vârfuri sunt conectate dacă există o cale între ele. Între timp Puternic conectat este aplicabil numai pentru grafice dirijate . Un subgraf al unui graf direcționat este considerat a fi un Componente puternic conectate (SCC) dacă și numai dacă pentru fiecare pereche de vârfuri A și B , există o cale de la A la B si o cale de la B la A . Să vedem de ce metoda standard dfs pentru a găsi componentele conectate într-un grafic nu poate fi folosit pentru a determina componente puternic conectate.

Luați în considerare următorul grafic:

Acum, să începem a dfs apel de la vârful 1 pentru a vizita alte vârfuri.

De ce metoda DFS convențională nu poate fi folosită pentru a găsi componentele puternic conectate?

Toate vârfurile pot fi atinse de la vârful 1. Dar vârfurile 1 și 5,6,7 nu pot fi în aceeași componentă puternic conectată deoarece nu există o cale direcționată de la vârful 5,6 sau 7 la vârful 1. Graficul are două puncte puternice. componentele conectate {1,2,3,4} și {5,6,7}. Deci metoda convențională dfs nu poate fi folosită pentru a găsi componentele puternic conectate.

Conectarea a două componente puternic conectate printr-o margine unidirecțională

Două componente conectate diferite devin o singură componentă dacă se adaugă o muchie între un vârf de la o componentă la un vârf al altei componente. Dar nu este cazul componentelor puternic conectate. Două componente puternic conectate nu devin o singură componentă puternic conectată dacă există doar o margine unidirecțională de la un SCC la altul SCC.

Abordarea forței brute pentru găsirea de componente puternic conectate

Metoda simplă va fi pentru fiecare vârf i (care nu face parte din nicio componentă puternică) găsiți vârfurile care vor fi partea componentei puternic conectate care conține vârful i. Două vârfuri i și j vor fi în aceeași componentă puternic conectată dacă există o cale direcționată de la vârful i la vârful j și invers.

Să înțelegem abordarea cu ajutorul următorului exemplu:

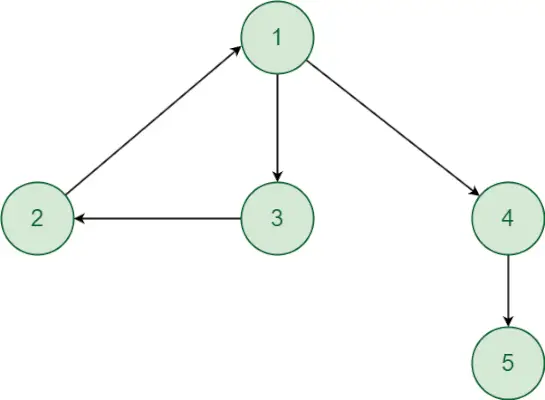
• Începând cu vârful 1. Există o cale de la vârful 1 la vârful 2 și invers. În mod similar, există o cale de la vârful 1 la vârful 3 și invers. Deci, vârfurile 2 și 3 vor fi în aceeași componentă puternic conectată ca vârful 1. Deși există o cale direcționată de la vârful 1 la vârful 4 și vârful 5. Dar nu există o cale direcționată de la vârful 4,5 la vârful 1, deci vârful 4 iar 5 nu va fi în aceeași componentă puternic conectată ca vârful 1. Astfel, vârfurile 1,2 și 3 formează o componentă puternic conectată.
• Pentru Vertex 2 și 3, Componenta puternic conectată a fost deja determinată.
• Pentru vârful 4, există o cale de la vârful 4 la vârful 5, dar nu există o cale de la vârful 5 la vârful 4. Deci vârfurile 4 și 5 nu vor fi în aceeași componentă puternic conectată. Deci, atât Vertex 4, cât și Vertex 5 vor face parte din Componenta Single Strongly Connected.
• Prin urmare, vor exista 3 componente puternic conectate {1,2,3}, {4} și {5}.

Mai jos este implementarea abordării de mai sus:

#include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector >& adj, vector & vis) { // Dacă nodul curr este destinația return true if (curr == des) { return true;  } vis[curr] = 1;  for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Pentru a spune dacă există o cale de la sursă la // destinație bool isPath(int src, int des, vector >& adj) { vector vis(adj.size() + 1, 0);  return dfs(src, des, adj, vis);  } // Funcție pentru a returna toată // componenta puternic conectată a unui grafic.  vector > findSCC(int n, vector >& a) { // Stochează toate componentele puternic conectate.  vector > ans;  // Stochează dacă un vârf este o parte a oricărui vector Componentă puternic // conectată is_scc(n + 1, 0);  vector > adj(n + 1);  pentru (int i = 0; i < a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i  <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector scc;  scc.push_back(i);  pentru (int j = i + 1; j <= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector > muchii{ { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  vector > ans = obj.findSCC(V, margini);  cout < < 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout  < < y  < < ' ';  }  cout  < < '
';  } } 

import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List > adj, Listă vis) { // Dacă nodul curr este destinația return true if (curr == des) { return true;  } vis.set(curr, 1);  for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Pentru a spune dacă există o cale de la sursă la // destinație boolean isPath(int src, int des, List > adj) { Listă vis = new ArrayList(adj.size() + 1);  pentru (int i = 0; i <= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List > findSCC(int n, List > a) { // Stochează toate componentele puternic conectate.  Listă > ans = new ArrayList();  // Stochează dacă un vârf face parte dintr-o listă de componente puternic // conectată is_scc = new ArrayList(n + 1);  pentru (int i = 0; i <= n; i++) {  is_scc.add(0);  }  List > adj = new ArrayList();  pentru (int i = 0; i <= n; i++) {  adj.add(new ArrayList());  }  for (List edge : a) { adj.get(edge.get(0)).add(edge.get(1));  } // Parcurgerea tuturor vârfurilor pentru (int i = 1; i <= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = new ArrayList();  scc.add(i);  pentru (int j = i + 1; j <= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List > margini = new ArrayList();  edges.add(new ArrayList(Lista.of(1, 3)));  edges.add(new ArrayList(Lista.of(1, 4)));  edges.add(new ArrayList(Lista.of(2, 1)));  edges.add(new ArrayList(Lista.of(3, 2)));  edges.add(new ArrayList(Lista.of(4, 5)));  Listă > ans = obj.findSCC(V, margini);  System.out.println('Componentele puternic conectate sunt:');  pentru (Lista x : ans) { for (int y : x) { System.out.print(y + ' ');  } System.out.println();  } } } // Acest cod este contribuit de shivamgupta310570>> Piton   C#   
using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List > adj, Listă vis) { // Dacă nodul curr este destinația, returnează adevărat dacă (curr == des) { returnează adevărat;  } vis[curr] = 1;  foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Pentru a spune dacă există o cale de la sursă la destinație public bool IsPath(int src, int des, List > adj) { var show = listă nouă (adj.Număr + 1);  pentru (int i = 0; i < adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List > FindSCC(int n, List > a) { // Stochează toate componentele puternic conectate var ans = listă nouă >();  // Stochează dacă un vârf face parte dintr-o componentă puternic conectată var isScc = listă nouă (n + 1);  pentru (int i = 0; i < n + 1; i++)  {  isScc.Add(0);  }  var adj = new List >(n + 1);  pentru (int i = 0; i < n + 1; i++)  {  adj.Add(new List ());  } pentru (int i = 0; i < a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i  <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Add(i);  pentru (int j = i + 1; j <= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List > margini = Listă nouă > { Listă nouă { 1, 3 }, listă nouă { 1, 4 }, listă nouă { 2, 1 }, listă nouă { 3, 2 }, listă nouă { 4, 5 } };  Listă > ans = obj.FindSCC(V, edges);  Console.WriteLine('Componentele puternic conectate sunt:');  foreach (var x in ans) { foreach (var y in x) { Consola.Scrie(y + ' ');  } Console.WriteLine();  } } } // Acest cod este contribuit de shivamgupta310570>> Javascript     
  Ieșire   
Strongly Connected Components are: 1 2 3 4 5 
  
    Complexitatea timpului: O(n * (n + m)),     deoarece pentru fiecare pereche de vârfuri verificăm dacă există o cale între ele.   
    Spațiu auxiliar: O(N)     
  
 Abordare eficientă pentru găsirea de componente puternic conectate (SCC)  
 
 Pentru a găsi SCC-uri într-un grafic, putem folosi algoritmi precum     Algoritmul lui Kosaraju     sau     Algoritmul lui Tarjan     . Să explorăm acești algoritmi pas cu pas.  
  
 1.    Algoritmul lui Kosaraju    :  
 
 Algoritmul lui Kosaraju implică două faze principale:  
  
 
    Efectuarea căutării în profunzime (DFS) pe graficul original     :  
 
 Mai întâi facem un DFS pe graficul original și înregistrăm timpii de terminare a nodurilor (adică, momentul la care DFS termină explorarea completă a unui nod).  
 
 
 
    Efectuarea DFS pe graficul transpus     :  
 
 Apoi inversăm direcția tuturor muchiilor din grafic pentru a crea graficul transpus.  
 
 În continuare, efectuăm un DFS pe graficul transpus, luând în considerare nodurile în ordinea descrescătoare a timpilor lor de sfârșit înregistrați în prima fază.  
 
 Fiecare traversare DFS în această fază ne va oferi un SCC.  
 
 
 
 
 Iată o versiune simplificată a algoritmului lui Kosaraju:  
  
 
    DFS pe graficul original     : Înregistrați timpii de terminare.  
 
    Transpuneți graficul     : inversează toate marginile.  
 
    DFS pe graficul transpus     : Procesează nodurile în ordinea descrescătoare a timpilor de terminare pentru a găsi SCC-uri.  
 
 
 2.   Algoritmul lui Tarjan   :  
 
 Algoritmul lui Tarjan este mai eficient deoarece găsește SCC-uri într-o singură trecere DFS folosind o stivă și o contabilitate suplimentară:  
  
 
    Traversare DFS     : În timpul DFS, mențineți un index pentru fiecare nod și cel mai mic index (valoare low-link) la care se poate ajunge din nod.  
 
    Grămadă     : Țineți evidența nodurilor aflate în prezent în stiva de recursivitate (o parte a SCC-ului curent în curs de explorare).  
 
    Identificarea SCC-urilor     : Când valoarea low-link a unui nod este egală cu indicele său, înseamnă că am găsit un SCC. Scoateți toate nodurile din stivă până ajungem la nodul curent.  
 
 
 Iată o schiță simplificată a algoritmului lui Tarjan:  
  
 
 Inițializați  index>  la 0.  
 
 Pentru fiecare nod nevizitat, executați DFS.  
 
 Setați indexul nodului și valoarea low-link.  
 
 Împingeți nodul pe stivă.  
 
 Pentru fiecare nod adiacent, fie efectuați DFS dacă nu este vizitat, fie actualizați valoarea low-link dacă se află în stivă.  
 
 Dacă valoarea low-link a nodului este egală cu indicele său, scoateți nodurile din stivă pentru a forma un SCC.  
 
 
 
 
 Concluzie  
 
 Înțelegerea și găsirea     componente puternic conectate     într-un grafic direcționat este esențial pentru multe aplicații în informatică.     a lui Kosaraju     și     a lui Tarjan     algoritmii sunt modalități eficiente de a identifica SCC, fiecare cu propria abordare și avantaje. Prin stăpânirea acestor concepte, puteți analiza și optimiza mai bine structura și comportamentul rețelelor complexe.