Având în vedere a BST , sarcina este de a căuta un nod în acesta BST .

Pentru a căuta o valoare în BST, considerați-o ca o matrice sortată. Acum putem efectua cu ușurință operația de căutare în BST folosind Algoritmul de căutare binar .

Algoritm pentru căutarea unei chei într-un arbore de căutare binar dat:

Să presupunem că vrem să căutăm numărul X, Începem de la rădăcină. Apoi:

• Comparăm valoarea de căutat cu valoarea rădăcinii.
  • Dacă este egal, am terminat cu căutarea dacă este mai mic, știm că trebuie să mergem la subarborele din stânga deoarece într-un arbore de căutare binar toate elementele din subarborele din stânga sunt mai mici și toate elementele din subarborele din dreapta sunt mai mari.
• Repetați pasul de mai sus până când nu mai este posibilă traversarea
• Dacă la orice iterație, cheia este găsită, returnați True. Altfel Fals.

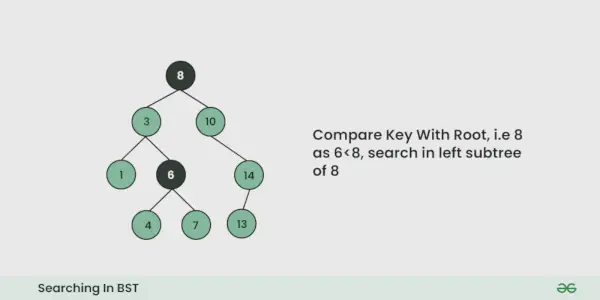
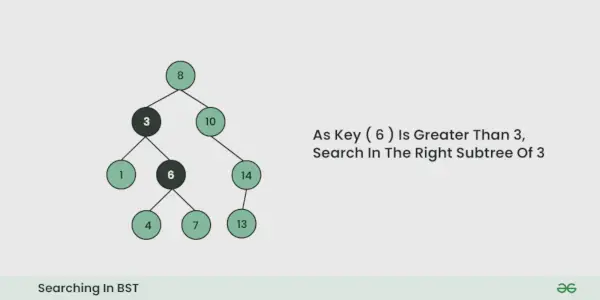
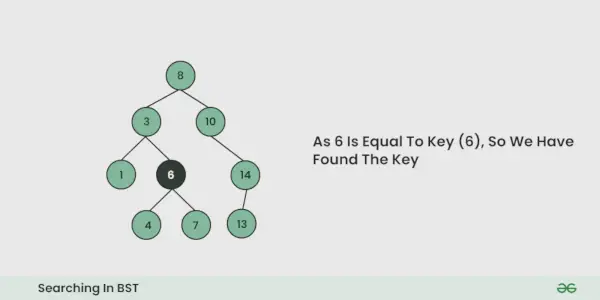
Ilustrație a căutării într-un BST:

Vezi ilustrația de mai jos pentru o mai bună înțelegere:

Program pentru implementarea căutării în BST:

C++

C

Java

>   
 
     
 
     
 
  
     
   
  
     
  
     
     
     
  
 
  
  
  
  
  # Python3 function to search a given key in a given BST>   class>   Node:>   >  # Constructor to create a new node>   >  def>   __init__(>  self>  , key):>   >  self>  .key>  =>   key>   >  self>  .left>  =>   None>   >  self>  .right>  =>   None>   # A utility function to insert>   # a new node with the given key in BST>   def>   insert(node, key):>   >  # If the tree is empty, return a new node>   >  if>   node>  is>   None>  :>   >  return>   Node(key)>   >  # Otherwise, recur down the tree>   >  if>   key   node.left = insert(node.left, key)  elif key>node.key: node.right = insert(node.right, key) # Returnează (neschimbat) indicatorul de nod return node # Funcție utilitar pentru a căuta o cheie într-o căutare BST def (rădăcină, cheie): # Cazuri de bază: root este nul sau cheia este prezentă la rădăcină dacă rădăcină este Niciunul sau root.key == cheie: return root # Cheia este mai mare decât cheia rădăcină dacă root.key return search(root.right, key) # Cheia este mai mică decât rădăcină Cheia 's return search(root.left, key) # Driver Code if __name__ == '__main__': root = None root = insert(root, 50) insert(root, 30) insert(root, 20) insert (rădăcină, 40) inserare (rădăcină, 70) inserare (rădăcină, 60) inserare (rădăcină, 80) # Cheie de găsit cheie = 6 # Căutare într-un BST dacă căutare (rădăcină, cheie) nu este None: print(cheie, 'not found') else: print(cheie, 'found') key = 60 # Căutare într-un BST dacă căutarea (rădăcină, cheie) nu este None: print(key, 'not found') else: print(cheie, 'găsit')>  
  
  
  
  
 
     
 
   
 
     
 
   
 
  
C# 
     
 
  
     
   
  
     
  
     
     
     
  
 
  
  
  
  
  // C# function to search a given key in a given BST>   using>   System;>   public>   class>   Node {>   >  public>   int>   key;>   >  public>   Node left, right;>   }>   public>   class>   BinaryTree {>   >  // A utility function to create a new BST node>   >  public>   Node NewNode(>  int>   item)>   >  {>   >  Node temp =>  new>   Node();>   >  temp.key = item;>   >  temp.left = temp.right =>  null>  ;>   >  return>   temp;>   >  }>   >  // A utility function to insert>   >  // a new node with given key in BST>   >  public>   Node Insert(Node node,>  int>   key)>   >  {>   >  // If the tree is empty, return a new node>   >  if>   (node ==>  null>  )>   >  return>   NewNode(key);>   >  // Otherwise, recur down the tree>   >  if>   (key   node.left = Insert(node.left, key);  else if (key>node.key) node.right = Insert(node.right, key);  // Returnează nodul de returnare a indicatorului de nod (neschimbat);  } // Funcție de utilitate pentru a căuta o cheie într-un nod public BST Căutare (rădăcină nod, cheie int) // Cazuri de bază: rădăcină este nulă sau cheia este prezentă la rădăcină dacă (rădăcină == null // Cod driver public static void Principal () { Node rădăcină = null; BinaryTree bt = new BinaryTree(); , 40); bt.Insert(root, 70); bt.Insert(root, 80); bt.Search(root, key) == null) Console.WriteLine(key + 'not found'); else Console.WriteLine(key + ' found'); if (bt.Search(root, key) == null) Console.WriteLine(key + ' not found'); else Console.WriteLine(key + ' found');  
  
  
  
  
 
     
 
  
>   
 
     
 
     
 
  
     
   
  
     
  
     
     
     
  
 
  
  
  
  
  // Javascript function to search a given key in a given BST>   class Node {>   >  constructor(key) {>   >  this>  .key = key;>   >  this>  .left =>  null>  ;>   >  this>  .right =>  null>  ;>   >  }>   }>   // A utility function to insert>   // a new node with given key in BST>   function>   insert(node, key) {>   >  // If the tree is empty, return a new node>   >  if>   (node ===>  null>  ) {>   >  return>   new>   Node(key);>   >  }>   >  // Otherwise, recur down the tree>   >  if>   (key   node.left = insert(node.left, key);  } else if (key>node.key) { node.right = insert(node.right, key);  } // Returnează nodul de returnare a indicatorului de nod (neschimbat); } // Funcție utilitar pentru a căuta o cheie într-o funcție BST search(root, key) { // Cazuri de bază: rădăcină este nulă sau cheia este prezentă la rădăcină dacă (rădăcină === null || root.key === cheie ) { returnează rădăcină;  } // Cheia este mai mare decât cheia rădăcină dacă (root.key return search(root.right, key); } // Cheia este mai mică decât cheia rădăcină return search(root.left, key); } // Driver Code let root = insert (rădăcină, 50); 60); insert (rădăcină, 80); găsit'); } else { console.log(key + ' found' } key = 60 // Căutare în BST if (search(root, key) === null(); key + ' not found' } else { console.log(key + ' found' }>'>).  
  
  
  
  
 
     
 
  
>   
 
     
 
      Complexitatea timpului:     O(h), unde h este înălțimea BST.   
    Spațiu auxiliar:     O(h), unde h este înălțimea BST. Acest lucru se datorează faptului că cantitatea maximă de spațiu necesară pentru stocarea stivei recursive ar fi     h     .  
  
    Linkuri conexe:        
  
  
   Operația de inserare a arborelui de căutare binar    
  
  Operația de ștergere a arborelui de căutare binar