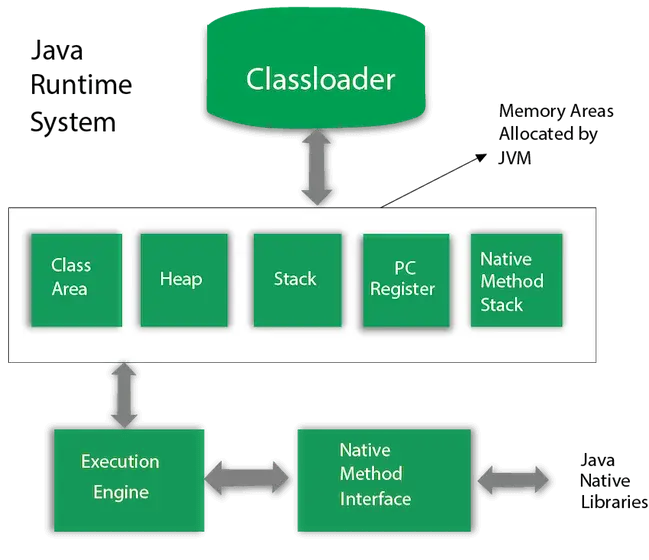
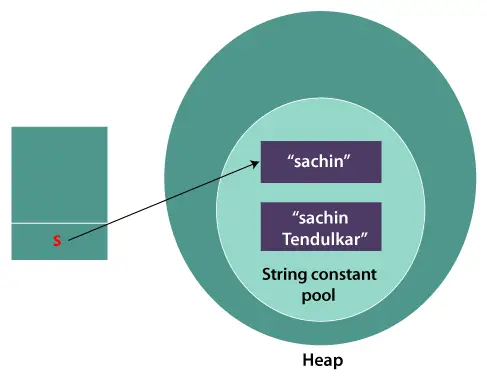
Model de filotaxis în Python | O unitate de botanică algoritmică

Filotaxia/filotaxia este aranjarea frunzelor pe tulpina unei plante, iar spiralele filotactice formează o clasă distinctivă de modele în natură. Cuvântul în sine provine din grecescul phullon care înseamnă „frunză” și taxis care înseamnă „aranjament”. Aranjamentele filotaxice florale de bază includ:
1. Filotaxie în spirală -
În filotaxia spirală, organele florale individuale sunt create într-un interval de timp regulat cu același unghi divergent. Unghiul divergent într-o floare cu filotaxie în spirală este de aproximativ 137,5 grade, ceea ce indică un model care urmează o
Seria Fibonacci
.Imaginea de mai jos arată modelele de filotaxie spirală având atât modele spiralate în sensul acelor de ceasornic, cât și în sens invers acelor de ceasornic.

Puncte importante de reținut:
- Serii Fibonacci descriu de obicei spiralele găsite în natură. Se calculează ca o serie în care perechea anterioară de numere se însumează cu următorul număr din serie. Seria este 1 1 2 3 5 8 13 21 34 55 89 … .
- Există de fapt un set de spirale în sensul acelor de ceasornic și unul în sens invers acelor de ceasornic.
- Spiralele organelor florale urmează un set de numărător și numitor de numere Fibonacci compensate (1/2 1/3 2/5 3/8 5/13 8/21 13/34 …). Numărătorul este numărul de ori sau întoarceri în jurul axei pentru a reveni la originea inițierii. Numitorul indică numărul de organe inițiate în timpul virajelor. Prin urmare, un 2/5 ar indica 2 rotații în jurul axei și 5 organe pentru a reveni la origine.
- ex. - La pin avem (2 3) (5 3) si (5 8) filotaxele in capituli perechile gasite sunt (21 34) (55 34) (55 89) si (89 144) iar la ananas cu solzi hexagonali tripletii (8 13 21) sau in functie de marimea exemplarului sunt gasite (34 21) .
- Prevalența secvenței Fibonacci în filotaxie este adesea denumită „misterul filotaxiei”.
Alte tipuri de aranjamente florale filotaxice sunt:
2. Filotaxie în spirală 3. Filotaxie în spirală simplă 4. Filotaxie în spirală complexă și 5. Filotaxie neregulată
Formarea modelului: Rezumat
Frumoasa aranjare a frunzelor din unele plante numită filotaxie se supune unui număr de relații matematice subtile. De exemplu, buchețelele din capul unei floarea-soarelui formează două spirale direcționate opus: 55 dintre ele în sensul acelor de ceasornic și 34 în sens invers acelor de ceasornic. În mod surprinzător
- Aceste numere sunt numere Fibonacci consecutive.
- Rapoartele numerelor Fibonacci alternative sunt date de convergentele la φ^(-2) unde φ este raportul de aur și se spune că măsoară fracția de rotație între frunzele succesive de pe tulpina unei plante:
- ex. : 1/2 pentru ulm si tei 1/3 pentru fag si alun 2/5 pentru stejar si mar 3/8 pentru plop si trandafir 5/13 pentru salcie si migdal etc.
- Fiecare frunză nouă de pe tulpina unei plante este poziționată la un anumit unghi față de cea anterioară și că acest unghi este constant între frunze: de obicei aproximativ 137,5 grade.
Adică dacă te uiți de sus la plantă și măsori unghiul format între o linie trasată de la tulpină la frunză și o linie corespunzătoare pentru frunza următoare, vei descoperi că există în general un unghi fix numit unghi de divergență. Aici suntem interesați de Spiral phyllotaxy și vom codifica pentru a forma un model Spiral Phyllotaxy în python folosind grafica țestoasă.
Proiectarea Codului
- Vom codifica două funcții, una pentru a desena modelul de filotaxie și cealaltă pentru a desena petalele.
- Petalele trebuie desenate numai după ce modelul de filotaxie este finalizat. Așa că vom apela funcția drawPetal() din interiorul funcției drawPhyllPattern(), ultimele coordonate x și y fiind vizitate după desenarea modelului de filotaxis.
- Funcția drawPetal() va desena petalele cu funcții și caracteristici ale broaștei testoase Programare broasca testoasa .
Pentru a codifica modelul de filotaxie trebuie să urmăm următoarele ecuații:
x = r*cos(θ)
y = r*sin(θ)
r θ can also vary - so the to form phyllotactic pattern we substitutethe cartesian form
by polar form:
r = c*sqrt(n)
θ = n*137.508°
 Reduces the problem to optimal packing on a disc so
Reduces the problem to optimal packing on a disc so
r = c*sqrt(n) is from the area of the circle
Area = πr² and n fills the Area in some units
c1 * n/π = r² c is 1/sqrt(c1/π)
So r = some constant c * sqrt(n)
PseudoCod: Model de filotaxis
IMPORT MODULES ( MATH TURTLE )
FUNCTION - DrawPhyllotaxisPattern( turtle t length petalstart angle = 137.508 size cspread)
turtleColor('Black')
FillColor(''Orange')
Convert angle to radians (Φ)
initialize ( xcenterycenter ) = ( 00 )
Drawing the Pattern Starts:
For n in Range ( 0t ):
r = cspread * sqrt(n)
θ = n * Φ
x = r * cos(θ) + xcenter
y = r * sin(θ) + ycenter
TURTLE POSITION(xy)
START DRAWING():
if Drawing pattern ends:
DrawFlowerPetals()
FUNCTION - DrawFlowerPetals(Turtle x coordinate y coordinate)
DRAW using Turtle methods
Create Turtle = gfg
Call DrawPhyllotaxisPattern( gfg t length petalstart angle = 137.508 size cspread)
END
Python Pattern APython Pattern Bimport math import turtle def drawPhyllPattern ( turtle t petalstart angle = 137.508 size = 2 cspread = 4 ): '''print a pattern of circles using spiral phyllotactic data''' # initialize position # turtle.pen(outline=1 pencolor='black' fillcolor='orange') turtle . color ( 'black' ) turtle . fillcolor ( 'orange' ) phi = angle * ( math . pi / 180.0 ) #we convert to radian xcenter = 0.0 ycenter = 0.0 # for loops iterate in this case from the first value until < 4 so for n in range ( 0 t ): r = cspread * math . sqrt ( n ) theta = n * phi x = r * math . cos ( theta ) + xcenter y = r * math . sin ( theta ) + ycenter # move the turtle to that position and draw turtle . up () turtle . setpos ( x y ) turtle . down () # orient the turtle correctly turtle . setheading ( n * angle ) if n > petalstart - 1 : turtle . color ( 'yellow' ) drawPetal ( turtle x y ) else : turtle . stamp () def drawPetal ( turtle x y ): turtle . penup () turtle . goto ( x y ) turtle . pendown () turtle . color ( 'black' ) turtle . fillcolor ( 'yellow' ) turtle . begin_fill () turtle . right ( 20 ) turtle . forward ( 70 ) turtle . left ( 40 ) turtle . forward ( 70 ) turtle . left ( 140 ) turtle . forward ( 70 ) turtle . left ( 40 ) turtle . forward ( 70 ) turtle . penup () turtle . end_fill () # this is needed to complete the last petal gfg = turtle . Turtle () gfg . shape ( 'turtle' ) gfg . speed ( 0 ) # make the turtle go as fast as possible drawPhyllPattern ( gfg 200 160 137.508 ) gfg . penup () gfg . forward ( 1000 )Ieșire:
Modele de filotaxis.

Creați un test