Max Heap în Python

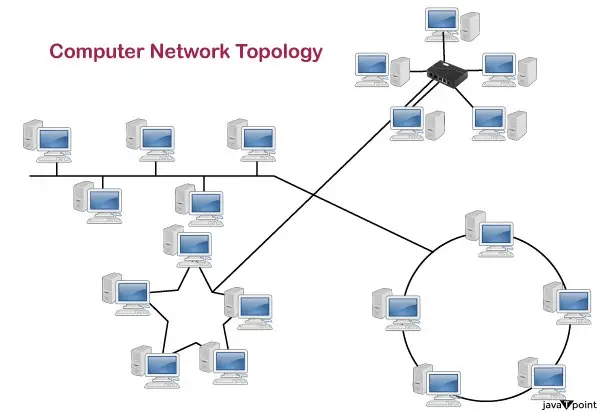
A Max-Heap este un arbore binar complet în care valoarea din fiecare nod intern este mai mare sau egală cu valorile din copiii acelui nod. Maparea elementelor unui heap într-o matrice este trivială: dacă un nod este stocat un index k, atunci copilul său din stânga este stocat la index 2k+1 și copilul său drept la index 2k+2 .
Exemple de Max Heap:

Cum este reprezentat Max Heap?
Un maxim Heap este un arbore binar complet. Un heap maxim este de obicei reprezentat ca o matrice. Elementul rădăcină va fi la Arr[0]. Tabelul de mai jos prezintă indici ai altor noduri pentru al-lea nod, adică Arr[i]:
- Arr[(i-1)/2] Returnează nodul părinte.
- Arr[(2*i)+1] Returnează nodul copil stâng.
- Arr[(2*i)+2] Returnează nodul secundar corect.
Operațiuni pe Max Heap:
- getMax() : returnează elementul rădăcină din Max Heap. Timpul Complexitatea acestei operațiuni este O(1) .
- extractMax() : elimină elementul maxim din MaxHeap. Timpul Complexitatea acestei operațiuni este O(log n) deoarece această operație trebuie să mențină proprietatea heap (prin apelarea heapify()) după eliminarea rădăcinii.
- introduce() : Introducerea unei noi chei ia O(log n) timp. Adăugăm o cheie nouă la capătul arborelui. Dacă noua cheie este mai mică decât cea părinte, atunci nu trebuie să facem nimic. În caz contrar, trebuie să traversăm în sus pentru a remedia proprietatea heap încălcată.
Notă: În implementarea de mai jos, facem indexare din indexul 1 pentru a simplifica implementarea.
Piton
# Python3 implementation of Max Heap> import> sys> class> MaxHeap:> > def> __init__(> self> , maxsize):> > > self> .maxsize> => maxsize> > self> .size> => 0> > self> .Heap> => [> 0> ]> *> (> self> .maxsize> +> 1> )> > self> .Heap[> 0> ]> => sys.maxsize> > self> .FRONT> => 1> > # Function to return the position of> > # parent for the node currently> > # at pos> > def> parent(> self> , pos):> > > return> pos> /> /> 2> > # Function to return the position of> > # the left child for the node currently> > # at pos> > def> leftChild(> self> , pos):> > > return> 2> *> pos> > # Function to return the position of> > # the right child for the node currently> > # at pos> > def> rightChild(> self> , pos):> > > return> (> 2> *> pos)> +> 1> > # Function that returns true if the passed> > # node is a leaf node> > def> isLeaf(> self> , pos):> > > if> pos>>>> self> .Heap[> self> .rightChild(pos)]):> > self> .swap(pos,> self> .leftChild(pos))> > self> .maxHeapify(> self> .leftChild(pos))> > # Swap with the right child and heapify> > # the right child> > else> :> > self> .swap(pos,> self> .rightChild(pos))> > self> .maxHeapify(> self> .rightChild(pos))> > # Function to insert a node into the heap> > def> insert(> self> , element):> > > if> self> .size>>>> self> .Heap[> self> .parent(current)]):> > self> .swap(current,> self> .parent(current))> > current> => self> .parent(current)> > # Function to print the contents of the heap> > def> Print> (> self> ):> > > for> i> in> range> (> 1> , (> self> .size> /> /> 2> )> +> 1> ):> > print> (> 'PARENT : '> +> str> (> self> .Heap[i])> +> > 'LEFT CHILD : '> +> str> (> self> .Heap[> 2> *> i])> +> > 'RIGHT CHILD : '> +> str> (> self> .Heap[> 2> *> i> +> 1> ]))> > # Function to remove and return the maximum> > # element from the heap> > def> extractMax(> self> ):> > popped> => self> .Heap[> self> .FRONT]> > self> .Heap[> self> .FRONT]> => self> .Heap[> self> .size]> > self> .size> -> => 1> > self> .maxHeapify(> self> .FRONT)> > > return> popped> # Driver Code> if> __name__> => => '__main__'> :> > > print> (> 'The maxHeap is '> )> > > maxHeap> => MaxHeap(> 15> )> > maxHeap.insert(> 5> )> > maxHeap.insert(> 3> )> > maxHeap.insert(> 17> )> > maxHeap.insert(> 10> )> > maxHeap.insert(> 84> )> > maxHeap.insert(> 19> )> > maxHeap.insert(> 6> )> > maxHeap.insert(> 22> )> > maxHeap.insert(> 9> )> > maxHeap.> Print> ()> > > print> (> 'The Max val is '> +> str> (maxHeap.extractMax()))> |
Ieșire
The maxHeap is PARENT : 84LEFT CHILD : 22RIGHT CHILD : 19 PARENT : 22LEFT CHILD : 17RIGHT CHILD : 10 PARENT : 19LEFT CHILD : 5RIGHT CHILD : 6 PARENT : 17LEFT CHILD : 3RIGHT CHILD : 9 The Max val is 84
Utilizarea funcțiilor Bibliotecii:
Folosim heapq clasă pentru a implementa Heap în Python. În mod implicit, Min Heap este implementat de această clasă. Dar înmulțim fiecare valoare cu -1, astfel încât să o putem folosi ca MaxHeap.
Python3
# Python3 program to demonstrate working of heapq> from> heapq> import> heappop, heappush, heapify> # Creating empty heap> heap> => []> heapify(heap)> # Adding items to the heap using heappush> # function by multiplying them with -1> heappush(heap,> -> 1> *> 10> )> heappush(heap,> -> 1> *> 30> )> heappush(heap,> -> 1> *> 20> )> heappush(heap,> -> 1> *> 400> )> # printing the value of maximum element> print> (> 'Head value of heap : '> +> str> (> -> 1> *> heap[> 0> ]))> # printing the elements of the heap> print> (> 'The heap elements : '> )> for> i> in> heap:> > print> ((> -> 1> *> i), end> => ' '> )> print> (> '
'> )> element> => heappop(heap)> # printing the elements of the heap> print> (> 'The heap elements : '> )> for> i> in> heap:> > print> (> -> 1> *> i, end> => ' '> )> |
Ieșire
Head value of heap : 400 The heap elements : 400 30 20 10 The heap elements : 30 10 20
Utilizarea funcțiilor Bibliotecă cu metoda dunder pentru numere, șiruri, tupluri, obiecte etc
Folosim heapq clasă pentru a implementa Heaps în Python. În mod implicit, Min Heap este implementat de această clasă.
Pentru a implementa MaxHeap nu limitându-ne doar la numere, ci la orice tip de obiect (String, Tuple, Object etc) ar trebui să
- Creați o clasă Wrapper pentru elementul din listă.
- Ignorați __lt__ metoda dunder pentru a da rezultat invers.
În continuare este implementarea metodei menționate aici.
Python3
'''> Python3 program to implement MaxHeap Operation> with built-in module heapq> for String, Numbers, Objects> '''> from> functools> import> total_ordering> import> heapq> |_+_| |