Arborele AVL:

Arborele AVL este un arbore de căutare binar cu auto-echilibrare ( BST ) unde diferența dintre înălțimile subarborilor din stânga și din dreapta nu poate fi mai mare de unu pentru toate nodurile.

Exemplu de arbore AVL:

Arborele de mai sus este AVL deoarece diferențele dintre înălțimile subarborilor din stânga și din dreapta pentru fiecare nod sunt mai mici sau egale cu 1.

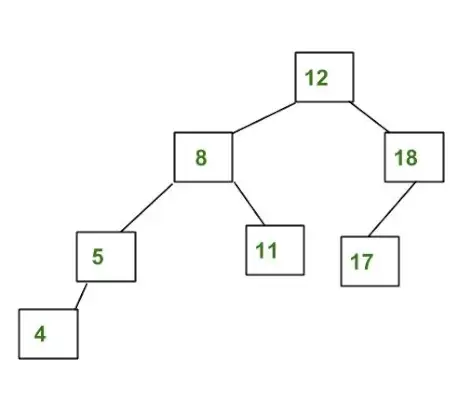
Exemplu de arbore care NU este un arbore AVL:

Arborele de mai sus nu este AVL deoarece diferențele dintre înălțimile subarborilor din stânga și din dreapta pentru 8 și 12 sunt mai mari decât 1.

De ce arbori AVL?

Majoritatea operațiunilor BST (de exemplu, căutare, max, min, inserare, ștergere etc.) iau Oh) timp unde h este înălțimea BST. Costul acestor operațiuni poate deveni Pe) Pentru o Arborele binar înclinat . Dacă ne asigurăm că înălțimea copacului rămâne O(log(n)) după fiecare inserare și ștergere, atunci putem garanta o limită superioară a O(log(n)) pentru toate aceste operațiuni. Înălțimea unui arbore AVL este întotdeauna O(log(n)) Unde n este numărul de noduri din arbore.

Inserare în arborele AVL:

Pentru a ne asigura că arborele dat rămâne AVL după fiecare inserare, trebuie să creștem operația standard de inserare BST pentru a efectua o reechilibrare.
Următoarele sunt două operațiuni de bază care pot fi efectuate pentru a echilibra un BST fără a încălca proprietatea BST (taste (stânga)

• Rotație la stânga
• Rotire dreapta

T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side) y x /  Right Rotation /  x T3 - - - - - - ->T1 și /  <- - - - - - - /  T1 T2 Left Rotation T2 T3 Keys in both of the above trees follow the following order keys(T1)  < key(x)  < keys(T2)  < key(y)  < keys(T3) So BST property is not violated anywhere. 

Practică recomandată Inserarea arborelui AVL Încercați!

Pași de urmat pentru inserare:

Fie nodul nou introdus În

• Efectuați standardul BST insert pentru În .
• Începând de la În , călătoriți sus și găsiți-l pe primul nod dezechilibrat . Lăsa Cu fi primul nod dezechilibrat, și fie copil de Cu care vine pe calea de la În la Cu și X fie nepotul de Cu care vine pe calea de la În la Cu .
• Reechilibrați arborele efectuând rotații adecvate pe subarborele înrădăcinat cu Cu. Pot exista 4 cazuri posibile care trebuie tratate ca X y și Cu poate fi aranjat în 4 moduri.
• Iată cele 4 posibile aranjamente:
  • y este copilul din stânga al lui z și x este copilul din stânga al lui y (cazul stânga stânga)
  • y este copilul din stânga al lui z și x este copilul din dreapta al lui y (cazul stânga dreapta)
  • y este copilul drept al lui z și x este copilul drept al lui y (cazul drept dreapta)
  • y este copilul din dreapta al lui z și x este copilul din stânga al lui y (cazul din dreapta stânga)

Următoarele sunt operațiunile care trebuie efectuate în cele 4 cazuri menționate mai sus. În toate cazurile, trebuie doar să o facem reechilibrare subarborele înrădăcinat cu Cu iar arborele complet devine echilibrat pe măsură ce înălțimea subarborelui (După rotații corespunzătoare) înrădăcinată cu Cu devine la fel ca înainte de inserare.

1. Stânga Stânga Casă

T1, T2, T3 and T4 are subtrees. z y /  /  y T4 Right Rotate (z) x z /  - - - - - - - - ->/  /  x T3 T1 T2 T3 T4 /  T1 T2 

2. Carcasa stânga dreapta

 z z x /  /  /  y T4 Left Rotate (y) x T4 Right Rotate(z) y z /  - - - - - - - - ->/  - - - - - - - -> /  /  T1 x y T3 T1 T2 T3 T4 /  /  T2 T3 T1 T2 

3. Carcasa dreapta dreapta

 z y /  /  T1 y Left Rotate(z) z x /  - - - - - - - ->/  /  T2 x T1 T2 T3 T4 /  T3 T4 

4. Carcasa Dreapta Stânga

 z z x /  /  /  T1 y Right Rotate (y) T1 x Left Rotate(z) z y /  - - - - - - - - ->/  - - - - - - - -> /  /  x T4 T2 y T1 T2 T3 T4 /  /  T2 T3 T3 T4 

Ilustrație a inserției la arborele AVL

Abordare:

Ideea este să folosim inserția recursivă BST, după inserare, obținem indicii către toți strămoșii unul câte unul într-o manieră de jos în sus. Deci nu avem nevoie de un indicator pentru părinte pentru a călători în sus. Codul recursiv însuși călătorește în sus și vizitează toți strămoșii nodului nou introdus.

Urmați pașii menționați mai jos pentru a implementa ideea:

• Faceți normalul Inserarea BST.
• Nodul curent trebuie să fie unul dintre strămoșii nodului nou introdus. Actualizați înălţime a nodului curent.
• Obțineți factorul de echilibru (înălțimea arborelui din stânga – înălțimea arborelui din dreapta) a nodului curent.
• Dacă factorul de echilibru este mai mare decât 1, atunci nodul curent este dezechilibrat și suntem fie în Stânga Stânga sau stânga Carcasa dreapta . Pentru a verifica dacă este minuscul stânga sau nu, comparați cheia nou introdusă cu cheia din rădăcină subarbore stângă .
• Dacă factorul de echilibru este mai mic decât -1 , atunci nodul curent este dezechilibrat și suntem fie în cazul Dreapta Dreapta, fie în cazul Dreapta-Stânga. Pentru a verifica dacă este cazul sau nu dreapta dreapta, comparați cheia nou introdusă cu cheia din rădăcina subarborescului din dreapta.

Mai jos este implementarea abordării de mai sus:

C++14

// C++ program to insert a node in AVL tree> #include> using> namespace> std;> > // An AVL tree node> class> Node> {> > public> :> > int> key;> > Node *left;> > Node *right;> > int> height;> };> > // A utility function to get the> // height of the tree> int> height(Node *N)> {> > if> (N == NULL)> > return> 0;> > return> N->înălţime;>>> > /* Helper function that allocates a> > new node with the given key and> > NULL left and right pointers. */> Node* newNode(> int> key)> {> > Node* node => new> Node();> > node->cheie = cheie;>>> node->dreapta = NULL;>>> > // added at leaf> > return> (node);> }> > // A utility function to right> // rotate subtree rooted with y> // See the diagram given above.> Node *rightRotate(Node *y)> {> > Node *x = y->stânga;>>> > // Perform rotation> > x->dreapta = y;>>> > // Update heights> > y->înălțime = max(înălțime (y->stânga),> > height(y->dreapta)) + 1;>>> > // Return new root> > return> x;> }> > // A utility function to left> // rotate subtree rooted with x> // See the diagram given above.> Node *leftRotate(Node *x)> {> > Node *y = x->dreapta;>>> > // Perform rotation> > y->stânga = x;>>> > // Update heights> > x->înălțime = max(înălțime (x->stânga),> > height(x->dreapta)) + 1;>>> > // Return new root> > return> y;> }> > // Get Balance factor of node N> int> getBalance(Node *N)> {> > if> (N == NULL)> > return> 0;> > return> height(N->stânga) - înălțime (N->dreapta);>>> else> if> (key>nod->cheie)>>> else> // Equal keys are not allowed in BST> > return> node;> > > /* 2. Update height of this ancestor node */> > node->înălțime = 1 + max(înălțime (nod->stânga),> > height(node->dreapta));>>> return> rightRotate(node);> > > // Right Right Case> > if> (balance node->dreapta->tasta)>>> {> > node->stânga = stângaRotire(nod->stânga);>>> {> > node->dreapta = dreaptaRotire(nod->dreapta);>>> stânga); precomandă(rădăcină->dreapta); } } // Cod driver int main() { Nod *root = NULL; /* Construirea arborelui dat în figura de mai sus */ root = insert(root, 10); rădăcină = insert (rădăcină, 20); rădăcină = insert (rădăcină, 30); rădăcină = insert(rădăcină, 40); rădăcină = insert (rădăcină, 50); rădăcină = insert (rădăcină, 25); /* Arborele AVL construit ar fi 30 / 20 40 / 10 25 50 */ cout < < 'Preorder traversal of the ' 'constructed AVL tree is '; preOrder(root); return 0; } // This code is contributed by // rathbhupendra>

C

// C program to insert a node in AVL tree> #include> #include> > // An AVL tree node> struct> Node> {> > int> key;> > struct> Node *left;> > struct> Node *right;> > int> height;> };> > // A utility function to get the height of the tree> int> height(> struct> Node *N)> {> > if> (N == NULL)> > return> 0;> > return> N->înălţime;>>> > /* Helper function that allocates a new node with the given key and> > NULL left and right pointers. */> struct> Node* newNode(> int> key)> {> > struct> Node* node = (> struct> Node*)> > malloc> (> sizeof> (> struct> Node));> > node->cheie = cheie;>>> node->dreapta = NULL;>>> > return> (node);> }> > // A utility function to right rotate subtree rooted with y> // See the diagram given above.> struct> Node *rightRotate(> struct> Node *y)> {> > struct> Node *x = y->stânga;>>> > // Perform rotation> > x->dreapta = y;>>> > // Update heights> > y->înălțime = max(înălțime (y->stânga),> > height(y->dreapta)) + 1;>>> > // Return new root> > return> x;> }> > // A utility function to left rotate subtree rooted with x> // See the diagram given above.> struct> Node *leftRotate(> struct> Node *x)> {> > struct> Node *y = x->dreapta;>>> > // Perform rotation> > y->stânga = x;>>> > // Update heights> > x->înălțime = max(înălțime (x->stânga),> > height(x->dreapta)) + 1;>>> > // Return new root> > return> y;> }> > // Get Balance factor of node N> int> getBalance(> struct> Node *N)> {> > if> (N == NULL)> > return> 0;> > return> height(N->stânga) - înălțime (N->dreapta);>>> else> if> (key>nod->cheie)>>> else> // Equal keys are not allowed in BST> > return> node;> > > /* 2. Update height of this ancestor node */> > node->înălțime = 1 + max(înălțime (nod->stânga),> > height(node->dreapta));>>> return> rightRotate(node);> > > // Right Right Case> > if> (balance node->dreapta->tasta)>>> {> > node->stânga = stângaRotire(nod->stânga);>>> {> > node->dreapta = dreaptaRotire(nod->dreapta);>>> , root->cheie);>>> preOrder(root->dreapta);>>> > ' tree is '> );> > preOrder(root);> > > return> 0;> }>

Java

// Java program for insertion in AVL Tree> class> Node {> > int> key, height;> > Node left, right;> > > Node(> int> d) {> > key = d;> > height => 1> ;> > }> }> > class> AVLTree {> > > Node root;> > > // A utility function to get the height of the tree> > int> height(Node N) {> > if> (N ==> null> )> > return> 0> ;> > > return> N.height;> > }> > > // A utility function to get maximum of two integers> > int> max(> int> a,> int> b) {> > return> (a>b) ? a:b;>>>

Python3

# Python code to insert a node in AVL tree> > # Generic tree node class> class> TreeNode(> object> ):> > def> __init__(> self> , val):> > self> .val> => val> > self> .left> => None> > self> .right> => None> > self> .height> => 1> > # AVL tree class which supports the> # Insert operation> class> AVL_Tree(> object> ):> > > # Recursive function to insert key in> > # subtree rooted with node and returns> > # new root of subtree.> > def> insert(> self> , root, key):> > > # Step 1 - Perform normal BST> > if> not> root:> > return> TreeNode(key)> > elif> key root.left = self.insert(root.left, key) else: root.right = self.insert(root.right, key) # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right)) # Step 3 - Get the balance factor balance = self.getBalance(root) # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance>1 și cheia returnează self.rightRotate (rădăcină) # Cazul 2 - Dreapta Dreapta dacă echilibru <-1 and key>root.right.val: return self.leftRotate(root) # Cazul 3 - Stânga Dreapta dacă echilibru> 1 și cheie> root.left.val: root.left = self.leftRotate(root.left) return self.rightRotate(rădăcină ) # Cazul 4 - Dreapta Stânga dacă este echilibrat <-1 and key root.right = self.rightRotate(root.right) return self.leftRotate(root) return root def leftRotate(self, z): y = z.right T2 = y.left # Perform rotation y.left = z z.right = T2 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def rightRotate(self, z): y = z.left T3 = y.right # Perform rotation y.right = z z.left = T3 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def getHeight(self, root): if not root: return 0 return root.height def getBalance(self, root): if not root: return 0 return self.getHeight(root.left) - self.getHeight(root.right) def preOrder(self, root): if not root: return print('{0} '.format(root.val), end='') self.preOrder(root.left) self.preOrder(root.right) # Driver program to test above function myTree = AVL_Tree() root = None root = myTree.insert(root, 10) root = myTree.insert(root, 20) root = myTree.insert(root, 30) root = myTree.insert(root, 40) root = myTree.insert(root, 50) root = myTree.insert(root, 25) '''The constructed AVL Tree would be 30 / 20 40 / 10 25 50''' # Preorder Traversal print('Preorder traversal of the', 'constructed AVL tree is') myTree.preOrder(root) print() # This code is contributed by Ajitesh Pathak>

C#

// C# program for insertion in AVL Tree> using> System;> > class> Node> {> > public> int> key, height;> > public> Node left, right;> > > public> Node(> int> d)> > {> > key = d;> > height = 1;> > }> }> > public> class> AVLTree> {> > > Node root;> > > // A utility function to get> > // the height of the tree> > int> height(Node N)> > {> > if> (N ==> null> )> > return> 0;> > > return> N.height;> > }> > > // A utility function to get> > // maximum of two integers> > int> max(> int> a,> int> b)> > {> > return> (a>b) ? a:b;>>>

Javascript

> > > // JavaScript program for insertion in AVL Tree> > class Node {> > constructor(d) {> > this> .key = d;> > this> .height = 1;> > this> .left => null> ;> > this> .right => null> ;> > }> > }> > > class AVLTree {> > constructor() {> > this> .root => null> ;> > }> > > // A utility function to get> > // the height of the tree> > height(N) {> > if> (N ==> null> )> return> 0;> > > return> N.height;> > }> > > // A utility function to get> > // maximum of two integers> > max(a, b) {> > return> a>b? a:b;>>>

Ieșire

Preorder traversal of the constructed AVL tree is 30 20 10 25 40 50 

Analiza complexității

Complexitatea timpului: O(log(n)), pentru inserare
Spațiu auxiliar: O(1)

Operațiile de rotație (rotire la stânga și la dreapta) durează constant, deoarece doar câteva indicatori sunt modificate acolo. Actualizarea înălțimii și obținerea factorului de echilibru necesită, de asemenea, timp constant. Deci, complexitatea de timp a inserției AVL rămâne aceeași cu inserția BST, care este O(h) unde h este înălțimea arborelui. Deoarece arborele AVL este echilibrat, înălțimea este O(Logn). Deci, complexitatea de timp a inserției AVL este O (Logn).

Comparație cu Red Black Tree:

Arborele AVL și alți arbori de căutare cu auto-echilibrare, cum ar fi Red Black, sunt utile pentru a realiza toate operațiunile de bază în timp O(log n). Arborii AVL sunt mai echilibrați în comparație cu arborii roșu-negru, dar pot provoca mai multe rotații în timpul inserării și ștergerii. Deci, dacă aplicația dvs. implică multe inserări și ștergeri frecvente, atunci arborii roșu negru ar trebui să fie preferați. Și dacă inserările și ștergerile sunt mai puțin frecvente și căutarea este operația mai frecventă, atunci arborele AVL ar trebui să fie preferat față de arborele negru roșu.

Mai jos este postarea pentru ștergere în arborele AVL:
Arbore AVL | Setul 2 (Ștergere)