Algoritmul Floyd Warshall
The Algoritmul Floyd-Warshall , numit după creatorii săi Robert Floyd și Stephen Warshall , este un algoritm fundamental în informatică și teoria grafurilor. Este folosit pentru a găsi cele mai scurte căi între toate perechile de noduri dintr-un grafic ponderat. Acest algoritm este foarte eficient și poate gestiona grafice cu ambele pozitiv si n greutăți de margine negative , ceea ce îl face un instrument versatil pentru rezolvarea unei game largi de probleme de rețea și conectivitate.
Cuprins
- Algoritmul Floyd Warshall
- Ideea din spatele algoritmului Floyd Warshall
- Algoritmul Floyd Warshall Algoritmul
- Pseudo-cod al algoritmului Floyd Warshall
- Ilustrație a algoritmului Floyd Warshall
- Analiza complexității algoritmului Floyd Warshall
- De ce algoritmul Floyd-Warshall este mai bun pentru graficele dense și nu pentru graficele rare?
- Întrebări importante la interviu legate de Floyd-Warshall
- Aplicații din lumea reală ale algoritmului Floyd-Warshall

Algoritmul Floyd Warshall:
The Algoritmul Floyd Warshall este un algoritm de calea cea mai scurtă, spre deosebire de toate perechile Dijkstra și Bellman Ford care sunt algoritmi cu calea cea mai scurtă cu o singură sursă. Acest algoritm funcționează atât pentru regizat și ponderat nedirecţionat grafice. Dar, nu funcționează pentru graficele cu cicluri negative (unde suma marginilor dintr-un ciclu este negativă). Urmează Programare dinamică abordare pentru a verifica fiecare cale posibilă care trece prin fiecare nod posibil pentru a calcula distanța cea mai scurtă dintre fiecare pereche de noduri.
Ideea din spatele algoritmului Floyd Warshall:
Să presupunem că avem un grafic G[][] cu ÎN vârfuri din 1 la N . Acum trebuie să evaluăm a shortestPathMatrix[][] unde s hortestPathMatrix[i][j] reprezintă calea cea mai scurtă între vârfuri i și j .
Evident, cea mai scurtă cale între i la j va avea unele k numărul de noduri intermediare. Ideea din spatele algoritmului floyd warshall este de a trata fiecare vârf din 1 la N ca un nod intermediar unul câte unul.
Următoarea figură arată proprietatea optimă a substructurii de mai sus în algoritmul floyd warshall:

Algoritmul Floyd Warshall Algoritmul:
- Inițializați matricea soluției la fel ca matricea graficului de intrare ca prim pas.
- Apoi actualizați matricea soluției considerând toate vârfurile ca un vârf intermediar.
- Ideea este de a alege toate nodurile unul câte unul și de a actualiza toate căile cele mai scurte care includ vârful ales ca vârf intermediar în calea cea mai scurtă.
- Când alegem numărul de vârf k ca vârf intermediar, am luat deja în considerare vârfurile {0, 1, 2, .. k-1} ca vârfuri intermediare.
- Pentru fiecare pereche (i, j) dintre vârfurile sursă și respectiv destinație, există două cazuri posibile.
- k nu este un vârf intermediar pe calea cea mai scurtă de la i la j . Păstrăm valoarea de dist[i][j] așa cum este.
- k este un vârf intermediar pe calea cea mai scurtă de la i la j . Actualizăm valoarea lui dist[i][j] la fel de dist[i][k] + dist[k][j], dacă dist[i][j]> dist[i][k] + dist[k][j]
Algoritmul Pseudo-Cod al lui Floyd Warshall: >
Pentru k = 0 până la n – 1
Pentru i = 0 până la n – 1
Pentru j = 0 până la n – 1
Distanța[i, j] = min(Distanța[i, j], Distanța[i, k] + Distanța[k, j])unde i = Nodul sursă, j = Nodul Destinație, k = Nodul Intermediar
Ilustrație a algoritmului Floyd Warshall:
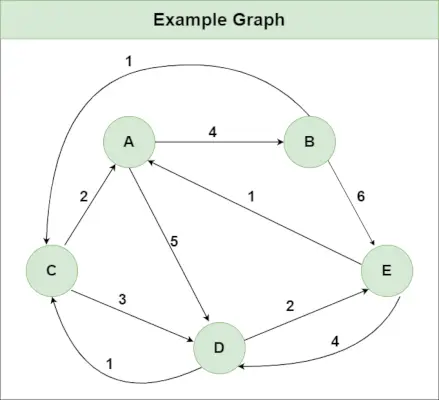
Practică recomandată Încercați!Să presupunem că avem un grafic așa cum se arată în imagine:

Pasul 1 : Inițializați matricea Distanță[][] folosind graficul de intrare astfel încât Distanța[i][j]= greutatea muchiei de la i la j , de asemenea Distanța[i][j] = Infinit dacă nu există margine de la i la j.

Pasul 2 : Trata nodul A ca nod intermediar și calculați Distanța[][] pentru fiecare pereche de noduri {i,j} folosind formula:
= Distanța[i][j] = minimă (Distanța[i][j], (Distanța de la i la A ) + (Distanța de la A la j))
= Distanța[i][j] = minimă (Distanța[i][j], Distanța[i][ A ] + Distanța[ A ][j])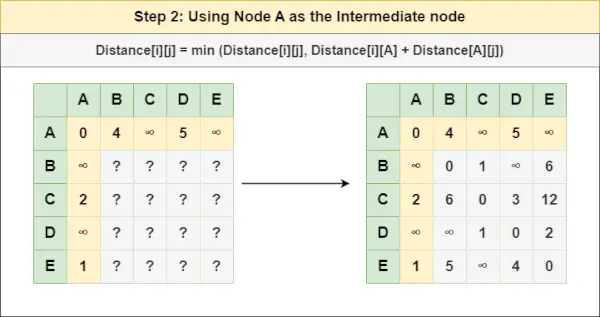
Pasul 3 : Trata nodul B ca nod intermediar și calculați Distanța[][] pentru fiecare pereche de noduri {i,j} folosind formula:
= Distanța[i][j] = minimă (Distanța[i][j], (Distanța de la i la B ) + (Distanța de la B la j))
= Distanța[i][j] = minimă (Distanța[i][j], Distanța[i][ B ] + Distanța[ B ][j])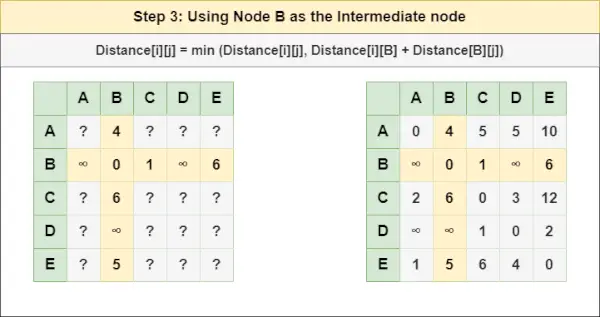
Pasul 4 : Trata nodul C ca nod intermediar și calculați Distanța[][] pentru fiecare pereche de noduri {i,j} folosind formula:
= Distanța[i][j] = minimă (Distanța[i][j], (Distanța de la i la C ) + (Distanța de la C la j))
= Distanța[i][j] = minimă (Distanța[i][j], Distanța[i][ C ] + Distanța[ C ][j])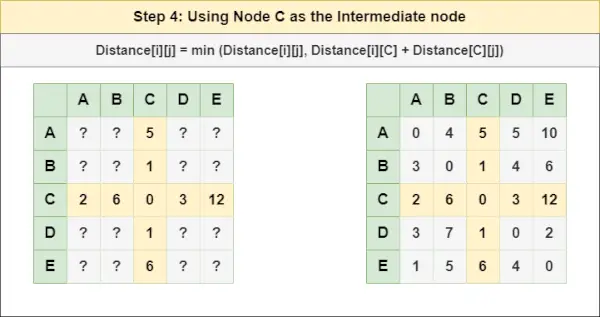
Pasul 5 : Trata nodul D ca nod intermediar și calculați Distanța[][] pentru fiecare pereche de noduri {i,j} folosind formula:
= Distanța[i][j] = minimă (Distanța[i][j], (Distanța de la i la D ) + (Distanța de la D la j))
= Distanța[i][j] = minimă (Distanța[i][j], Distanța[i][ D ] + Distanța[ D ][j])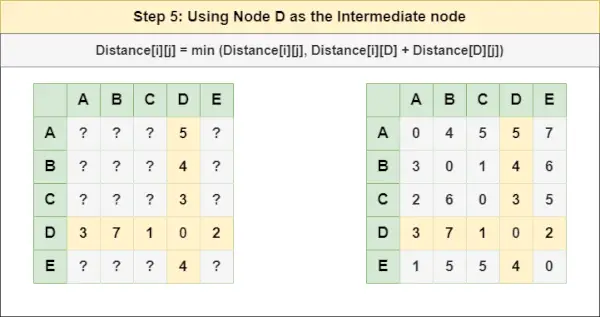
Pasul 6 : Trata nodul ȘI ca nod intermediar și calculați Distanța[][] pentru fiecare pereche de noduri {i,j} folosind formula:
= Distanța[i][j] = minimă (Distanța[i][j], (Distanța de la i la ȘI ) + (Distanța de la ȘI la j))
= Distanța[i][j] = minimă (Distanța[i][j], Distanța[i][ ȘI ] + Distanța[ ȘI ][j])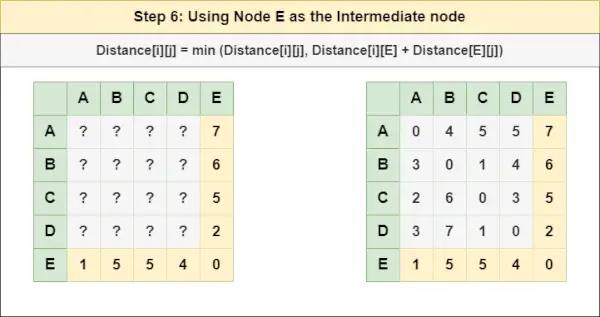
Pasul 7 : Deoarece toate nodurile au fost tratate ca un nod intermediar, acum putem returna matricea Distanță[][] actualizată ca matrice de răspuns.

Mai jos este implementarea abordării de mai sus:
C++ // C++ Program for Floyd Warshall Algorithm #include using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Înainte de începerea unei iterații, avem cele mai scurte distanțe între toate perechile de vârfuri, astfel încât cele mai scurte distanțe să considere doar vârfurile din mulțimea {0, 1, 2, .. k-1} ca vârfuri intermediare. ----> După terminarea unei iterații, vârful nr. k se adaugă la mulțimea vârfurilor intermediare și mulțimea devine {0, 1, 2, .. k} */ pentru (k = 0; k < V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path from // i to j, then update the value of // dist[i][j] if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Imprimă cea mai scurtă distanță matrice printSolution(dist); } /* O funcție utilitar pentru a tipări soluția */ void printSolution(int dist[][V]) { cout < < 'The following matrix shows the shortest ' 'distances' ' between every pair of vertices
'; for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { if (dist[i][j] == INF) cout < < 'INF' < < ' '; else cout < < dist[i][j] < < ' '; } cout < < endl; } } // Driver's code int main() { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } }; // Apelul funcției floydWarshall(graph); întoarce 0; } // Acest cod este contribuit de Mythri J L>>> C (3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1}, { INF, INF, INF, 0}}; // Apelul funcției floydWarshall(graph); întoarce 0; }>>> Java (3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } }; AllPairShortestPath a = nou AllPairShortestPath(); // Apel de funcție a.floydWarshall(graph); } } // A contribuit de Aakash Hasija>>> Python3 Înainte de începerea unei iterații, avem cele mai scurte distanțe între toate perechile de vârfuri, astfel încât cele mai scurte distanțe să considere doar vârfurile din mulțimea {0, 1, 2, .. k-1} ca vârfuri intermediare. ----> După terminarea unei iterații, vârful nr. k se adaugă la mulțimea de vârfuri intermediare și mulțimea devine {0, 1, 2, .. k} ''' pentru k în intervalul (V): # alegeți toate vârfurile ca sursă unul câte unul pentru i în range(V): # Alegeți toate vârfurile ca destinație pentru # sursa aleasă mai sus pentru j în intervalul (V): # Dacă vârful k este pe calea cea mai scurtă de la # i la j, atunci actualizați valoarea dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # O funcție utilitar pentru a tipări soluția def printSolution (dist): print('Următoarea matrice arată cele mai scurte distanțe între fiecare pereche de vârfuri') pentru i în interval (V): pentru j în interval (V): if(dist[i][j] == INF): print('%7s' % ('INF'), final=' ') else: print('%7d ' % (dist[i][j]), end=' ') if j == V-1: print() # Codul driverului if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 ''' grafic = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Apelul funcției floydWarshall(graph) # Acest cod este contribuit de Mythri J L C# // C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath { readonly static int INF = 99999, V = 4; void floydWarshall(int[, ] graph) { int[, ] dist = new int[V, V]; int i, j, k; // Initialize the solution matrix // same as input graph matrix // Or we can say the initial // values of shortest distances // are based on shortest paths // considering no intermediate // vertex for (i = 0; i < V; i++) { for (j = 0; j < V; j++) { dist[i, j] = graph[i, j]; } } /* Add all vertices one by one to the set of intermediate vertices. --->Înainte de începerea unei iterații, avem cele mai scurte distanțe între toate perechile de vârfuri, astfel încât cele mai scurte distanțe să considere doar vârfurile din mulțimea {0, 1, 2, .. k-1} ca vârfuri intermediare. ---> După terminarea unei iterații, vârful nr. k se adaugă la mulțimea vârfurilor intermediare și mulțimea devine {0, 1, 2, .. k} */ pentru (k = 0; k < V; k++) { // Pick all vertices as source // one by one for (i = 0; i < V; i++) { // Pick all vertices as destination // for the above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest // path from i to j, then update // the value of dist[i][j] if (dist[i, k] + dist[k, j] < dist[i, j]) { dist[i, j] = dist[i, k] + dist[k, j]; } } } } // Print the shortest distance matrix printSolution(dist); } void printSolution(int[, ] dist) { Console.WriteLine( 'Following matrix shows the shortest ' + 'distances between every pair of vertices'); for (int i = 0; i < V; ++i) { for (int j = 0; j < V; ++j) { if (dist[i, j] == INF) { Console.Write('INF '); } else { Console.Write(dist[i, j] + ' '); } } Console.WriteLine(); } } // Driver's Code public static void Main(string[] args) { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int[, ] grafic = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } }; AllPairShortestPath a = nou AllPairShortestPath(); // Apel de funcție a.floydWarshall(graph); } } // Acest articol este contribuit de // Abdul Mateen Mohammed Javascript // A JavaScript program for Floyd Warshall All // Pairs Shortest Path algorithm. var INF = 99999; class AllPairShortestPath { constructor() { this.V = 4; } floydWarshall(graph) { var dist = Array.from(Array(this.V), () =>nou Array(this.V).fill(0)); var i, j, k; // Inițializați matricea soluției // la fel ca și matricea graficului de intrare // Sau putem spune că // valorile inițiale ale celor mai scurte distanțe // se bazează pe cele mai scurte căi // luând în considerare niciun punct intermediar // pentru (i = 0; i < this.V; i++) { for (j = 0; j < this.V; j++) { dist[i][j] = graph[i][j]; } } /* Add all vertices one by one to the set of intermediate vertices. --->Înainte de începerea unei iterații, avem cele mai scurte distanțe între toate perechile de vârfuri, astfel încât cele mai scurte distanțe să considere doar vârfurile din mulțimea {0, 1, 2, .. k-1} ca vârfuri intermediare. ---> După terminarea unei iterații, vârful nr. k se adaugă la mulțimea vârfurilor intermediare și mulțimea devine {0, 1, 2, .. k} */ pentru (k = 0; k < this.V; k++) { // Pick all vertices as source // one by one for (i = 0; i < this.V; i++) { // Pick all vertices as destination // for the above picked source for (j = 0; j < this.V; j++) { // If vertex k is on the shortest // path from i to j, then update // the value of dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) { dist[i][j] = dist[i][k] + dist[k][j]; } } } } // Print the shortest distance matrix this.printSolution(dist); } printSolution(dist) { document.write( 'Following matrix shows the shortest ' + 'distances between every pair of vertices ' ); for (var i = 0; i < this.V; ++i) { for (var j = 0; j < this.V; ++j) { if (dist[i][j] == INF) { document.write(' INF '); } else { document.write(' ' + dist[i][j] + ' '); } } document.write(' '); } } } // Driver Code /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ var grafic = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ]; var a = nou AllPairShortestPath(); // Imprimă soluția a.floydWarshall(graph); // Acest cod este contribuit de rdtaank.>>> PHP (3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ $graph = array(array(0, 5, $INF, 10), array($INF, 0, 3, $INF), array($ INF, $INF, 0, 1), matrice ($INF, $INF, $INF, 0)); // Apelul funcției floydWarshall($graph, $V, $INF); // Acest cod este contribuit de Ryuga ?> Ieșire
The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0
Analiza complexității algoritmului Floyd Warshall:
- Complexitatea timpului: O(V 3 ), unde V este numărul de vârfuri din grafic și rulăm trei bucle imbricate fiecare cu dimensiunea V
- Spațiu auxiliar: O(V 2 ), pentru a crea o matrice 2-D pentru a stoca cea mai scurtă distanță pentru fiecare pereche de noduri.
Notă : Programul de mai sus tipărește doar cele mai scurte distanțe. Putem modifica soluția pentru a imprima cele mai scurte căi și prin stocarea informațiilor predecesorului într-o matrice 2D separată.
De ce algoritmul Floyd-Warshall este mai bun pentru graficele dense și nu pentru graficele rare?
Graficul dens : Un grafic în care numărul de muchii este semnificativ mult mai mare decât numărul de vârfuri.
Grafic rar : Un grafic în care numărul de muchii este foarte mic.Indiferent de câte muchii există în grafic Algoritmul Floyd Warshall rulează pentru O(V 3 ) ori prin urmare este cel mai potrivit pentru Grafice dense . În cazul graficelor rare, Algoritmul lui Johnson este mai potrivit.
Întrebări importante de interviu legate de Floyd-Warshall:
- Cum se detectează ciclul negativ într-un grafic folosind algoritmul Floyd Warshall?
- Cum este algoritmul Floyd-warshall diferit de algoritmul lui Dijkstra?
- Cum este algoritmul Floyd-warshall diferit de algoritmul Bellman-Ford?
Aplicații în lumea reală ale algoritmului Floyd-Warshall:
- În rețelele de calculatoare, algoritmul poate fi folosit pentru a găsi calea cea mai scurtă între toate perechile de noduri dintr-o rețea. Aceasta este denumită ca rutarea rețelei .
- Conectivitate de zbor În industria aviației pentru a găsi cea mai scurtă cale între aeroporturi.
- GIS ( Sisteme Informaţionale Geografice ) aplicațiile implică adesea analiza datelor spațiale, cum ar fi rețelele de drumuri, pentru a găsi cele mai scurte căi între locații.
- algoritmul lui Kleene care este o generalizare a lui Floyd Warshall, poate fi folosită pentru a găsi expresii regulate pentru un limbaj obișnuit.