BUCKET SORT - STRUCTURI DE DATE ȘI TUTORIALE PENTRU ALGORITMI - TECHCODEVIEW.COM

Sortare cu găleată este o tehnică de sortare care implică împărțirea elementelor în diferite grupuri, sau găleți. Aceste găleți sunt formate prin distribuirea uniformă a elementelor. Odată ce elementele sunt împărțite în găleți, acestea pot fi sortate folosind orice alt algoritm de sortare. În cele din urmă, elementele sortate sunt adunate împreună într-o manieră ordonată.

Algoritmul de sortare al găleților:

Crea n goliți găleți (Sau liste) și faceți următoarele pentru fiecare element de matrice arr[i].

Introduceți arr[i] în bucket[n*array[i]]
Sortați găleți individuale folosind sortarea prin inserție.
Concatenează toate gălețile sortate.

Cum funcționează Bucket Sort?

Pentru a aplica sortarea găleților pe matricea de intrare [0,78, 0,17, 0,39, 0,26, 0,72, 0,94, 0,21, 0,12, 0,23, 0,68] , urmam acești pași:

Pasul 1: Creați o matrice de dimensiunea 10, în care fiecare slot reprezintă o găleată.

Crearea de găleți pentru sortare

Pasul 2: Inserați elemente în găleți din matricea de intrare în funcție de intervalul lor.

Introducerea elementelor în găleți:

Luați fiecare element din tabloul de intrare.
Înmulțiți elementul cu dimensiunea matricei de găleți (10 în acest caz). De exemplu, pentru elementul 0,23, obținem 0,23 * 10 = 2,3.
Convertiți rezultatul într-un număr întreg, care ne oferă indicele găleții. În acest caz, 2.3 este convertit în întregul 2.
Introduceți elementul în găleată corespunzătoare indicelui calculat.
Repetați acești pași pentru toate elementele din matricea de intrare.

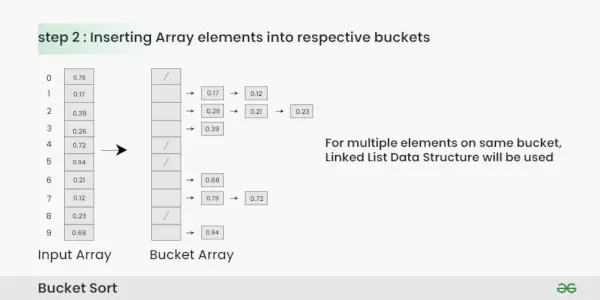
Inserarea elementelor Array în gălețile respective

Pasul 3: Sortați elementele din fiecare găleată. În acest exemplu, folosim sortarea rapidă (sau orice algoritm de sortare stabil) pentru a sorta elementele din fiecare găleată.

Sortarea elementelor din fiecare găleată:

Aplicați un algoritm de sortare stabil (de exemplu, Sortare cu bule, Sortare îmbinare) pentru a sorta elementele din fiecare grupă.
Elementele din fiecare găleată sunt acum sortate.

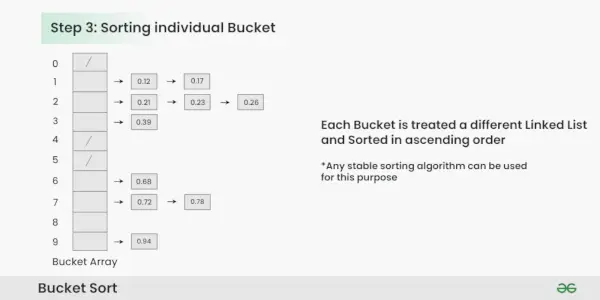
Sortare găleată individuală

Pasul 4: Adunați elementele din fiecare găleată și puneți-le înapoi în matricea originală.

Adunarea elementelor din fiecare găleată:

Repetați fiecare găleată în ordine.
Introduceți fiecare element individual din găleată în matricea originală.
Odată ce un element este copiat, acesta este scos din găleată.
Repetați acest proces pentru toate gălețile până când toate elementele au fost adunate.

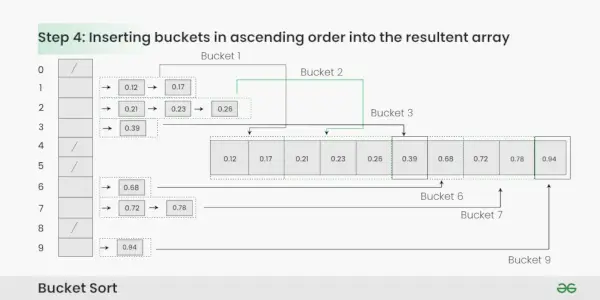
Inserarea găleților în ordine crescătoare în matricea rezultată

Pasul 5: Matricea originală conține acum elementele sortate.

Matricea sortată finală folosind sortarea găleților pentru intrarea dată este [0.12, 0.17, 0.21, 0.23, 0.26, 0.39, 0.68, 0.72, 0.78, 0.94].

Returnează matricea sortată

Implementarea algoritmului de sortare a găleților:

Mai jos este implementarea pentru sortarea găleții:

C++

  #include  #include  using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector & găleată) { pentru (int i = 1; i < bucket.size(); ++i) {  float key = bucket[i];  int j = i - 1;  while (j>= 0 && găleată[j]> cheie) { găleată[j + 1] = găleată[j];  j--;  } găleată[j + 1] = cheie;  } } // Funcție pentru a sorta arr[] de dimensiunea n folosind bucket sort void bucketSort(float arr[], int n) { // 1) Creați n vector de găleți goale b[n];  // 2) Pune elemente de matrice în diferite compartimente pentru (int i = 0; i < n; i++) {  int bi = n * arr[i];  b[bi].push_back(arr[i]);  }  // 3) Sort individual buckets using insertion sort  for (int i = 0; i  < n; i++) {  insertionSort(b[i]);  }  // 4) Concatenate all buckets into arr[]  int index = 0;  for (int i = 0; i  < n; i++) {  for (int j = 0; j  < b[i].size(); j++) {  arr[index++] = b[i][j];  }  } } // Driver program to test above function int main() {  float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434};  int n = sizeof(arr) / sizeof(arr[0]);  bucketSort(arr, n);  cout  < < 'Sorted array is 
';  for (int i = 0; i  < n; i++) {  cout  < < arr[i]  < < ' ';  }  return 0; }

Java

  import java.util.ArrayList; import java.util.List; public class Main {  // Insertion sort function to sort individual buckets  public static void insertionSort(List găleată) { for (int i = 1; i < bucket.size(); ++i) {  float key = bucket.get(i);  int j = i - 1;  while (j>= 0 && bucket.get(j)> key) { bucket.set(j + 1, bucket.get(j));  j--;  } bucket.set(j + 1, cheie);  } } // Funcție de sortare arr[] de dimensiunea n folosind bucket sort public static void bucketSort(float[] arr) { int n = arr.length;  // 1) Creați n listă de găleți goale [] buckets = new ArrayList[n];  pentru (int i = 0; i < n; i++) {  buckets[i] = new ArrayList();  }  // 2) Put array elements in different buckets  for (int i = 0; i  < n; i++) {  int bi = (int) (n * arr[i]);  buckets[bi].add(arr[i]);  }  // 3) Sort individual buckets using insertion sort  for (int i = 0; i  < n; i++) {  insertionSort(buckets[i]);  }  // 4) Concatenate all buckets into arr[]  int index = 0;  for (int i = 0; i  < n; i++) {  for (int j = 0; j  < buckets[i].size(); j++) {  arr[index++] = buckets[i].get(j);  }  }  }  // Driver program to test above function  public static void main(String[] args) {  float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f};  bucketSort(arr);  System.out.println('Sorted array is:');  for (float num : arr) {  System.out.print(num + ' ');  }  } }

Piton

  def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 și bucket[j]> cheie: bucket[j + 1] = bucket[j] j -= 1 bucket[j + 1] = key def bucket_sort(arr): n = len(arr) buckets = [[] pentru _ în interval(n)] # Pune elemente de matrice în diferite găleți pentru num în arr: bi = int(n * num) găleți[bi].append(num) # Sortează găleți individuale folosind sortarea inserției pentru găleți în găleți: insertion_sort (găleată) # Concatenați toate gălețile în arr[] index = 0 pentru găleată în găleți: pentru num în găleată: arr[index] = num index += 1 arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434] (arr) print('Matricea sortată este:') print(' '.join(map(str, arr)))

  using System; using System.Collections.Generic; class Program {  // Insertion sort function to sort individual buckets  static void InsertionSort(List găleată) { for (int i = 1; i < bucket.Count; ++i)  {  float key = bucket[i];  int j = i - 1;  while (j>= 0 && găleată[j]> cheie) { găleată[j + 1] = găleată[j];  j--;  } găleată[j + 1] = cheie;  } } // Funcție de sortare arr[] de dimensiunea n folosind bucket sort static void BucketSort(float[] arr) { int n = arr.Length;  // 1) Creați n listă de găleți goale [] găleți = Listă nouă [n];  pentru (int i = 0; i < n; i++)  {  buckets[i] = new List ();  } // 2) Pune elemente de matrice în diferite compartimente pentru (int i = 0; i < n; i++)  {  int bi = (int)(n * arr[i]);  buckets[bi].Add(arr[i]);  }  // 3) Sort individual buckets using insertion sort  for (int i = 0; i  < n; i++)  {  InsertionSort(buckets[i]);  }  // 4) Concatenate all buckets into arr[]  int index = 0;  for (int i = 0; i  < n; i++)  {  for (int j = 0; j  < buckets[i].Count; j++)  {  arr[index++] = buckets[i][j];  }  }  }  // Driver program to test above function  static void Main(string[] args)  {  float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f };  BucketSort(arr);  Console.WriteLine('Sorted array is:');  foreach (float num in arr)  {  Console.Write(num + ' ');  }  } }

JavaScript

  function insertionSort(bucket) {  for (let i = 1; i  < bucket.length; ++i) {  let key = bucket[i];  let j = i - 1;  while (j>= 0 && găleată[j]> cheie) { găleată[j + 1] = găleată[j];  j--;  } găleată[j + 1] = cheie;  } } function bucketSort(arr) { let n = arr.length;  let buckets = Array.from({lungime: n}, () => []);  // Pune elemente de matrice în diferite găleți pentru (fie i = 0; i < n; i++) {  let bi = Math.floor(n * arr[i]);  buckets[bi].push(arr[i]);  }  // Sort individual buckets using insertion sort  for (let i = 0; i  < n; i++) {  insertionSort(buckets[i]);  }  // Concatenate all buckets into arr[]  let index = 0;  for (let i = 0; i  < n; i++) {  for (let j = 0; j  < buckets[i].length; j++) {  arr[index++] = buckets[i][j];  }  } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));

Ieșire

Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897

Analiza complexității algoritmului de sortare a găleților:

Complexitatea timpului: Pe ² ),

Dacă presupunem că inserarea într-o găleată durează O(1) timp, atunci pașii 1 și 2 ai algoritmului de mai sus iau în mod clar O(n) timp.
O(1) este ușor posibil dacă folosim o listă legată pentru a reprezenta o găleată.
Pasul 4 necesită, de asemenea, timp O(n), deoarece vor fi n articole în toate gălețile.
Pasul principal de analizat este pasul 3. Acest pas necesită, de asemenea, timp O(n) în medie dacă toate numerele sunt distribuite uniform.

Spațiu auxiliar: O(n+k)