Viteza este pur și simplu așa cum cunoașteți măsura cât de repede sau încet se mișcă un obiect, cum ar fi cât de repede conduceți o mașină. Acum, aici vorbim de un anumit tip de viteză. Viteza unghiulară este doar un tip de viteză, dar aici corpul trebuie să se miște pe o cale circulară.

Formula vitezei unghiulare

Viteza unghiulară este definită ca rata de modificare a deplasării unghiulare, adică unghiul parcurs de un corp de-a lungul unei căi circulare. Viteza unghiulară este calculată în funcție de un număr de rotații/revoluții efectuate de un corp la timpul necesar. Viteza unghiulară este desemnată cu litera greacă, „ω” cunoscută sub numele de Omega. Unitatea SI a vitezei unghiulare este rad/s.

Viteza unghiulară este calculată folosind două formule diferite,

ω = θ/t ω = v/r

Derivarea formulei

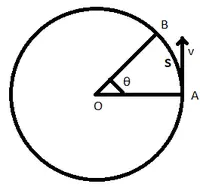
Să considerăm un corp care se deplasează pe o cale circulară cu raza r prezentată mai sus cu o viteză liniară v. Să presupunem că corpul se deplasează din punctul A în B acoperind o distanță s prin arcul de cerc și traversând un unghi θ în perioada de timp t.

Cale circulară acoperită de un corp

După cum se știe, viteza unghiulară este rata de schimbare a deplasării – Viteza unghiulară, ω = θ/t

Deci formula pentru viteza unghiulară este ω = θ/t .

O altă formulă pentru viteza unghiulară

În ciuda formulei menționate mai sus, există o altă formulă și mai utilizată pentru calcularea vitezei unghiulare din punctul de vedere al examenelor de concurs.

Ca ω = θ/t ⇢ (1)

Acum știm că distanța deplasată de-a lungul arcului de cerc este egală cu raza înmulțită cu unghiul parcurs. Asa de,

s = rθ

=> θ = s/r ⇢ (2)

De la (1) și (2),

ω = s/(rt) ⇢ (3)

De asemenea, din înțelegerea generală a vitezelor liniare,

v = s/t ⇢ (4)

De la (3) și (4),

ω = v/r

Exemple de probleme

Întrebarea 1: Luați în considerare un corp care se mișcă pe o cale circulară cu raza de 5 m. Acoperă jumătate de revoluție în 5 secunde. Calculați-i viteza unghiulară.

Soluţie:

În jumătate de rotație, unghiul parcurs este de 180 de grade. În radiani, este egal cu π radiani.

ω = θ/t

=> ω = π/5 = 0,628 rad/s

Întrebarea 2: O roată de mașină cu raza de 2m se rotește cu o viteză liniară de 10m/s. Calculați viteza unghiulară.

Soluţie:

ω = v/r

ω = 10/2

= 5 rad/s

Întrebarea 3: Luați în considerare o mașină de curse care se deplasează pe o pistă circulară cu o viteză de 18 km/h și raza pistei este de 0,2 m. Calculați viteza unghiulară a mașinii.

Soluţie:

v = 18 km/h = 5 m/s

r = 0,2 m

ω = v/r

= 5/0,2

= 25 rad/s

Întrebarea 4: O mașină se deplasează pe o cale circulară cu raza de 2m cu o viteză unghiulară de 2 rad/s. Calculați unghiul în grade prin care mașina se mișcă în 2s.

Soluţie:

Dat, ω = 2 rad/s și t = 2s

Deoarece ω = θ/t => θ = ωt

=> θ = (2 × 2) = 4 rad

În grade, θ = 4 × (180/π) = 229,18 grade

Întrebarea 5: Câte rotații a făcut un corp deplasându-se pe o cale circulară cu o viteză unghiulară de 7π rad/s în 0,5s?

Soluţie:

Având în vedere ω = 7π rad/s și t = 0,5s

Deoarece ω = θ/t => θ = ωt

θ = (7π × 0,5) = 3,5π

În 2π rad, rotațiile acoperite sunt 1

=> În 1 rad, revoluția acoperită este (1/2π)

=> În 3,5π rad, rotații = 3,5π/2π = 1,75 rotații

Deci, corpul va efectua 1 rotație completă și 3/4 din următoarea revoluție într-o perioadă de timp de 0,5 s.

Întrebarea 6: Care va fi viteza unghiulară a unui corp care se deplasează pe o cale circulară cu raza de 2m care acoperă 4m de lungime a arcului 5s.

Soluţie:

Având în vedere s = 4m, r = 2m, t = 5s

Folosind formula s = rθ => θ = s/r

θ = 4/2 = 2 rad

Deoarece ω = θ/t

=> ω = 2/5 = 0,4 rad/s