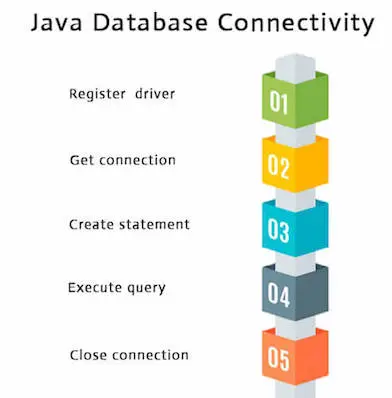
Treliças:

Seja L um conjunto não vazio fechado sob duas operações binárias chamadas meet and join, denotadas por ∧ e ∨. Então L é chamado de rede se os seguintes axiomas forem válidos onde a, b, c são elementos em L:
1) Lei Comutativa: -
(a) a ∧ b = b ∧ a (b) a ∨ b = b ∨ a
2) Direito Associativo: -
(a) (a ∧ b)∧ c = a ∧(b∧ c) (b) (a ∨ b) ∨ c = a ∨ (b ∨ c)
3) Lei de Absorção: -
(a) a ∧ ( a ∨ b) = a (b) a ∨ ( a ∧ b) = a
Dualidade:
O dual de qualquer afirmação em uma rede (L,∧ ,∨ ) é definido como uma afirmação obtida pela troca de ∧ e ∨.
Por exemplo , o dual de a ∧ (b ∨ a) = a ∨ a é a ∨ (b ∧ a )= a ∧ a
Redes limitadas:
Uma rede L é chamada de rede limitada se tiver o maior elemento 1 e o menor elemento 0.
Exemplo:
- O conjunto de potências P(S) do conjunto S sob as operações de interseção e união é um reticulado limitado, pois ∅ é o menor elemento de P(S) e o conjunto S é o maior elemento de P(S).
- O conjunto de +ve inteiro I + sob a ordem usual de ≦ não é uma rede limitada, pois tem o menor elemento 1, mas o maior elemento não existe.
Propriedades de redes limitadas:
Se L é uma rede limitada, então para qualquer elemento a ∈ L, temos as seguintes identidades:
- uma ∨ 1 = 1
- uma ∧1= uma
- uma ∨0=uma
- uma ∧0=0
Teorema: Prove que toda rede finita L = {a 1 ,a 2 ,a 3 ....a n } é limitado.
Prova: Demos a rede finita:
eu = {uma 1 ,a 2 ,a 3 ....a n }
Assim, o maior elemento das redes L é um 1 ∨ um 2 ∨ um 3∨....∨a n .
Além disso, o menor elemento da rede L é um 1 ∧ uma 2 ∧a 3 ∧....∧a n .
Desde então, os maiores e menores elementos existem para cada rede finita. Portanto, L é limitado.
Sub-redes:
Considere um subconjunto não vazio L 1 de uma rede L. Então L 1 é chamado de sub-rede de L se L 1 em si é uma rede, ou seja, a operação de L, ou seja, a ∨ b ∈ L 1 e a ∧ b ∈ L 1 sempre que um ∈ L 1 eb ∈ eu 1 .
Exemplo: Considere a rede de todos os + cinco inteiros I + sob a operação de divisibilidade. A treliça D n de todos os divisores de n > 1 é uma sub-rede de I + .
Determine todas as sub-redes de D 30 que contêm pelo menos quatro elementos, D 30 ={1,2,3,5,6,10,15,30}.
Solução: As sub-redes de D 30 que contêm pelo menos quatro elementos são os seguintes:
1. {1, 2, 6, 30} 2. {1, 2, 3, 30}
3. {1, 5, 15, 30} 4. {1, 3, 6, 30}
5. {1, 5, 10, 30} 6. {1, 3, 15, 30}
7. {2, 6, 10, 30}
Redes Isomórficas:
Duas treliças L 1 e eu 2 são chamadas de redes isomórficas se houver uma bijeção de L 1 para mim 2 ou seja, f: L 1 ⟶ eu 2 , tal que f (a ∧ b) =f(a)∧ f(b) e f (a ∨ b) = f (a) ∨ f (b)
Exemplo: Determine se as redes mostradas na fig são isomórficas.
Solução: As redes mostradas na fig são isomórficas. Considere o mapeamento f = {(a, 1), (b, 2), (c, 3), (d, 4)}. Por exemplo f (b ∧ c) = f (a) = 1. Além disso, nós tem f (b) ∧ f (c) = 2 ∧ 3 = 1

Rede Distributiva:
Uma rede L é chamada de rede distributiva se, para quaisquer elementos a, b e c de L, ela satisfaz as seguintes propriedades distributivas:
- a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)
- a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)
Se a rede L não satisfaz as propriedades acima, ela é chamada de rede não distributiva.
Exemplo:
- O conjunto de potências P (S) do conjunto S sob a operação de interseção e união é uma função distributiva. Desde,
uma ∩ (b ∪ c) = (a ∩ b) ∪ (a ∩ c)
e, também a ∪ (b ∩ c) = (a ∪ b) ∩ (a ∪c) para quaisquer conjuntos a, b e c de P(S). - A rede mostrada na fig. II é distributiva. Visto que satisfaz as propriedades distributivas para todos os triplos ordenados que são obtidos de 1, 2, 3 e 4.

Complementos e reticulados complementados:
Seja L uma rede limitada com limite inferior o e limite superior I. Seja a um elemento se L. Um elemento x em L é chamado de complemento de a se a ∨ x = I e a ∧ x = 0
Dizemos que uma rede L é complementada se L for limitada e todo elemento de L tiver um complemento.
Exemplo: Determine o complemento de a e c na fig:

Solução: O complemento de a é d. Visto que, a ∨ d = 1 e a ∧ d = 0
O complemento de c não existe. Visto que não existe nenhum elemento c tal que c ∨ c'=1 e c ∧ c'= 0.
Malha Modular:
Uma rede (L, ∧,∨) é chamada de rede modular se a ∨ (b ∧ c) = (a ∨ b) ∧ c sempre que a ≦ c.
Produto direto de redes:
Deixe (L 1 ∨ 1 ∧ 1 )e eu 2 ∨ 2 ∧ 2 ) sejam duas redes. Então (L, ∧,∨) é o produto direto das redes, onde L = L 1 xL 2 em que a operação binária ∨(join) e ∧(meet) em L são tais que para qualquer (a 1 ,b 1 )e (um 2 ,b 2 ) em L.
(a 1 ,b 1 )∨(uma 2 ,b 2 )=(uma 1 ∨ 1 a 2 ,b 1 ∨ 2 b 2 )
e (um 1 ,b 1 ) ∧ (uma 2 ,b 2 )=(uma 1 ∧ 1 a 2 ,b 1 ∧ 2 b 2 ).
Exemplo: Considere uma rede (L, ≦) conforme mostrado na fig. onde eu = {1, 2}. Determine as redes (L 2 , ≦), onde eu 2 =L x L.

Solução: A treliça (L 2 , ≦) é mostrado na fig: