Conversão de código binário para BCD

O código BCD desempenha um papel importante nos circuitos digitais. O BCD significa Número Decimal Codificado Binário. No código BCD, cada dígito do número decimal é representado como seu número binário equivalente. Portanto, o LSB e o MSB dos números decimais são representados como seus números binários. Existem as seguintes etapas para converter o número binário em BCD:
- Primeiro, converteremos o número binário em decimal.
- Converteremos o número decimal em BCD.
Vamos dar um exemplo para entender o processo de conversão de um número binário em BCD
Exemplo 1: (11110) 2
1. Primeiro, converta o número binário fornecido em um número decimal.
Número binário: (11110) 2
Encontrando o equivalente decimal do número:
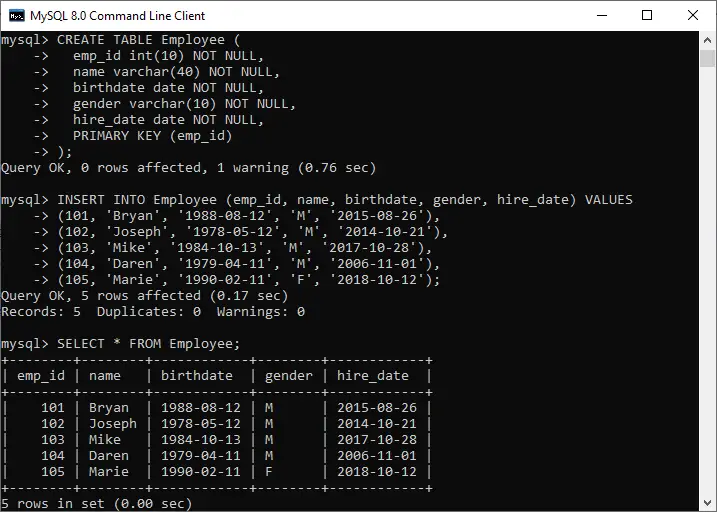
| Passos | Número binário | Número decimal |
|---|---|---|
| 1) | (11110) 2 | ((1 × 2 4 ) + (1 × 2 3 ) + (1 × 2 2 ) + (1 × 2 1 ) + (0 × 2 0 )) 10 |
| 2) | (11110) 2 | (16 + 8 + 4 + 2 + 0) 10 |
| 3) | (11110) 2 | (30) 10 |
Número decimal do número binário (11110) 2 é (30) 10
2. Agora, convertemos o decimal para BCD
Convertemos cada dígito do número decimal em grupos do número binário de quatro bits.
| Passos | Número decimal | Conversão |
|---|---|---|
| Passo 1 | 30 10 | (0011) 2 (0000) 2 |
| Passo 2 | 30 10 | (00110000) BCD |
Resultado:
(11110) 2 = (00110000) BCD
Abaixo está a tabela que contém o código BCD do número decimal e binário.
| Código binário | Número decimal | Código BCD |
|---|---|---|
| A B C D | B 4 :B 3 B 2 B 1 B 0 | |
| 0 0 0 0 | 0 | 0: 0 0 0 0 |
| 0 0 0 1 | 1 | 0: 0 0 0 1 |
| 0 0 1 0 | 2 | 0: 0 0 1 0 |
| 0 0 1 1 | 3 | 0: 0 0 1 1 |
| 0 1 0 0 | 4 | 0: 0 1 0 0 |
| 0 1 0 1 | 5 | 0: 0 1 0 1 |
| 0 1 1 0 | 6 | 0: 0 1 1 0 |
| 0 1 1 1 | 7 | 0: 0 1 1 1 |
| 1 0 0 0 | 8 | 0: 1 0 0 0 |
| 1 0 0 1 | 9 | 0: 1 0 0 1 |
| 1 0 1 0 | 10 | 1: 0 0 0 0 |
| 1 0 1 1 | onze | 1: 0 0 0 1 |
| 1 1 0 0 | 12 | 1: 0 0 1 0 |
| 1 1 0 1 | 13 | 1: 0 0 1 1 |
| 1 1 1 0 | 14 | 1: 0 1 0 0 |
| 1 1 1 1 | quinze | 1: 0 1 0 1 |
Na tabela acima, o bit mais significativo do número decimal é representado pelo bit B4, e os bits menos significativos são representados por B3, B2, B1 e B0. A partir da tabela acima, podemos expressar a função SOP para diferentes bits do código BCD da seguinte forma:

Os mapas K das funções SOP acima são os seguintes:





Conversão de BCD para binário
O processo de conversão do código BCD em binário é oposto ao processo de conversão do código binário em BCD. Existem as seguintes etapas para converter o código BCD em binário:
Na primeira etapa, vamos converter o número BCD em decimal, formando os grupos de quatro bits e encontrando o número decimal equivalente para cada grupo.
Na última etapa, converteremos um número decimal em binário usando o processo de conversão de número decimal em binário.
Exemplo 1: (00101000) BCD
1) Converter BCD em decimal
Faça os grupos de 4 dígitos e encontre o número decimal equivalente como:
| Passos | Número BCD | Conversão |
|---|---|---|
| Passo 1 | (00101000) BCD | (0010) 2 (1000) 2 |
| Passo 2 | (00101000) BCD | (2) 10 (8) 10 |
| etapa 3 | (00101000) BCD | (28) 10 |
O número decimal do código BCD fornecido é: (28) 10
2. Converter Decimal em Binário
Use o método de divisão longa para converter o número decimal em um número binário como:
| Passos | Operação | Resultado | Restante |
|---|---|---|---|
| 1. | 28/2 | 14 | 0 |
| 2. | 14/2 | 7 | 0 |
| 3. | 02/07 | 3 | 1 |
| 4. | 3/2 | 1 | 1 |
| 5. | 1/2 | 0 | 1 |
Organize os restos na ordem inversa. Portanto, o LSB do número binário é o primeiro resto, e o MSB do número binário é o último resto.
O número binário do número decimal (18) 10 é: (11100) 2
Resultado:
(00101000) BCD = (11100) 2