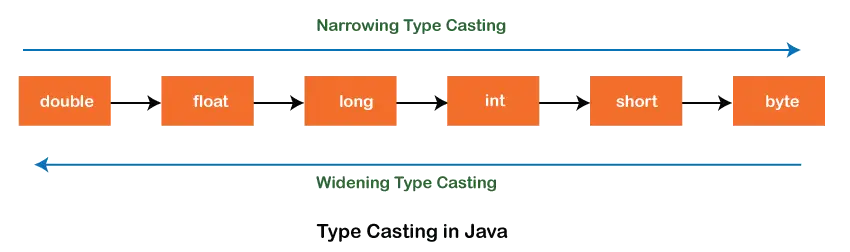
Całkowite pokrycie wszystkich zer w macierzy binarnej

 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; } Biorąc pod uwagę macierz binarną, która zawiera tylko zera i jedynki, musimy znaleźć sumę pokrycia wszystkich zer macierzy, gdzie pokrycie dla konkretnego 0 jest zdefiniowane jako całkowita liczba jedynek wokół zera w kierunkach od lewej do prawej w górę i w dół. Te mogą znajdować się w dowolnym miejscu, aż do punktu narożnego w określonym kierunku.
Przykłady:
Input : mat[][] = {0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0} Output : 20 First four zeros are surrounded by only one 1. So coverage for zeros in first row is 1 + 1 + 1 + 1 Zeros in second row are surrounded by three 1's. Note that there is no 1 above. There are 1's in all other three directions. Coverage of zeros in second row = 3 + 3. Similarly counting for others also we get overall count as below. 1 + 1 + 1 + 1 + 3 + 3 + 2 + 2 + 2 + 2 + 2 = 20 Input : mat[][] = {1 1 1 0 1 0 0 1} Output : 8 Coverage of first zero is 2 Coverages of other two zeros is 3 Total coverage = 2 + 3 + 3 = 8 Recommended Practice Pokrycie wszystkich zer w macierzy binarnej Spróbuj! A proste rozwiązanie aby rozwiązać ten problem, należy niezależnie liczyć jedynki wokół zer, tj. wykonujemy pętlę cztery razy w każdym kierunku dla każdej komórki danej macierzy. Ilekroć w dowolnej pętli znajdziemy 1, przerywamy pętlę i zwiększamy wynik o 1.
Jakiś wydajne rozwiązanie jest wykonanie następujących czynności.
- Przejdź przez wszystkie wiersze od lewej do prawej, zwiększ wynik, jeśli 1 jest już widoczna (w bieżącym przejściu), a bieżący element ma wartość 0.
- Przejdź przez wszystkie wiersze od prawej do lewej, zwiększając wynik, jeśli 1 jest już widoczna (w bieżącym przejściu), a bieżący element ma wartość 0.
- Przejrzyj wszystkie kolumny od góry do dołu, zwiększ wynik, jeśli 1 jest już widoczna (w bieżącym przejściu), a bieżący element ma wartość 0.
- Przejrzyj wszystkie kolumny od dołu do góry, zwiększ wynik, jeśli 1 jest już widoczna (w bieżącym przejściu), a bieżący element ma wartość 0.
W poniższym kodzie brana jest zmienna logiczna isOne, która staje się prawdziwa w momencie napotkania jedynki w bieżącym przejściu dla wszystkich zer, po czym wynik iteracji jest zwiększany o jedną tę samą procedurę, która jest stosowana we wszystkich czterech kierunkach, aby uzyskać ostateczną odpowiedź. Po każdym przejściu resetujemy isOne do wartości false.
C++ // C++ program to get total coverage of all zeros in // a binary matrix #include using namespace std ; #define R 4 #define C 4 // Returns total coverage of all zeros in mat[][] int getTotalCoverageOfMatrix ( int mat [ R ][ C ]) { int res = 0 ; // looping for all rows of matrix for ( int i = 0 ; i < R ; i ++ ) { bool isOne = false ; // 1 is not seen yet // looping in columns from left to right // direction to get left ones for ( int j = 0 ; j < C ; j ++ ) { // If one is found from left if ( mat [ i ][ j ] == 1 ) isOne = true ; // If 0 is found and we have found // a 1 before. else if ( isOne ) res ++ ; } // Repeat the above process for right to // left direction. isOne = false ; for ( int j = C -1 ; j >= 0 ; j -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns for up and down // directions. for ( int j = 0 ; j < C ; j ++ ) { bool isOne = false ; // 1 is not seen yet for ( int i = 0 ; i < R ; i ++ ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( int i = R -1 ; i >= 0 ; i -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } // Driver code to test above methods int main () { int mat [ R ][ C ] = {{ 0 0 0 0 } { 1 0 0 1 } { 0 1 1 0 } { 0 1 0 0 } }; cout < < getTotalCoverageOfMatrix ( mat ); return 0 ; }
Java // Java program to get total // coverage of all zeros in // a binary matrix import java . io . * ; class GFG { static int R = 4 ; static int C = 4 ; // Returns total coverage // of all zeros in mat[][] static int getTotalCoverageOfMatrix ( int [][] mat ) { int res = 0 ; // looping for all // rows of matrix for ( int i = 0 ; i < R ; i ++ ) { // 1 is not seen yet boolean isOne = false ; // looping in columns from // left to right direction // to get left ones for ( int j = 0 ; j < C ; j ++ ) { // If one is found // from left if ( mat [ i ][ j ] == 1 ) isOne = true ; // If 0 is found and we // have found a 1 before. else if ( isOne ) res ++ ; } // Repeat the above // process for right // to left direction. isOne = false ; for ( int j = C - 1 ; j >= 0 ; j -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns // for up and down directions. for ( int j = 0 ; j < C ; j ++ ) { // 1 is not seen yet boolean isOne = false ; for ( int i = 0 ; i < R ; i ++ ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( int i = R - 1 ; i >= 0 ; i -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } // Driver code static public void main ( String [] args ) { int [][] mat = {{ 0 0 0 0 } { 1 0 0 1 } { 0 1 1 0 } { 0 1 0 0 }}; System . out . println ( getTotalCoverageOfMatrix ( mat )); } } // This code is contributed by anuj_67.
Python3 # Python3 program to get total coverage of all zeros in # a binary matrix R = 4 C = 4 # Returns total coverage of all zeros in mat[][] def getTotalCoverageOfMatrix ( mat ): res = 0 # looping for all rows of matrix for i in range ( R ): isOne = False # 1 is not seen yet # looping in columns from left to right # direction to get left ones for j in range ( C ): # If one is found from left if ( mat [ i ][ j ] == 1 ): isOne = True # If 0 is found and we have found # a 1 before. else if ( isOne ): res += 1 # Repeat the above process for right to # left direction. isOne = False for j in range ( C - 1 - 1 - 1 ): if ( mat [ i ][ j ] == 1 ): isOne = True else if ( isOne ): res += 1 # Traversing across columns for up and down # directions. for j in range ( C ): isOne = False # 1 is not seen yet for i in range ( R ): if ( mat [ i ][ j ] == 1 ): isOne = True else if ( isOne ): res += 1 isOne = False for i in range ( R - 1 - 1 - 1 ): if ( mat [ i ][ j ] == 1 ): isOne = True else if ( isOne ): res += 1 return res # Driver code mat = [[ 0 0 0 0 ][ 1 0 0 1 ][ 0 1 1 0 ][ 0 1 0 0 ]] print ( getTotalCoverageOfMatrix ( mat )) # This code is contributed by shubhamsingh10
C# // C# program to get total coverage // of all zeros in a binary matrix using System ; class GFG { static int R = 4 ; static int C = 4 ; // Returns total coverage of all zeros in mat[][] static int getTotalCoverageOfMatrix ( int [] mat ) { int res = 0 ; // looping for all rows of matrix for ( int i = 0 ; i < R ; i ++ ) { // 1 is not seen yet bool isOne = false ; // looping in columns from left to // right direction to get left ones for ( int j = 0 ; j < C ; j ++ ) { // If one is found from left if ( mat [ i j ] == 1 ) isOne = true ; // If 0 is found and we // have found a 1 before. else if ( isOne ) res ++ ; } // Repeat the above process for // right to left direction. isOne = false ; for ( int j = C - 1 ; j >= 0 ; j -- ) { if ( mat [ i j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns // for up and down directions. for ( int j = 0 ; j < C ; j ++ ) { // 1 is not seen yet bool isOne = false ; for ( int i = 0 ; i < R ; i ++ ) { if ( mat [ i j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( int i = R - 1 ; i >= 0 ; i -- ) { if ( mat [ i j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } // Driver code to test above methods static public void Main () { int [] mat = {{ 0 0 0 0 } { 1 0 0 1 } { 0 1 1 0 } { 0 1 0 0 }}; Console . WriteLine ( getTotalCoverageOfMatrix ( mat )); } } // This code is contributed by vt_m.
JavaScript < script > // Javascript program to get total // coverage of all zeros in // a binary matrix let R = 4 ; let C = 4 ; // Returns total coverage // of all zeros in mat[][] function getTotalCoverageOfMatrix ( mat ) { let res = 0 ; // looping for all // rows of matrix for ( let i = 0 ; i < R ; i ++ ) { // 1 is not seen yet let isOne = false ; // looping in columns from // left to right direction // to get left ones for ( let j = 0 ; j < C ; j ++ ) { // If one is found // from left if ( mat [ i ][ j ] == 1 ) isOne = true ; // If 0 is found and we // have found a 1 before. else if ( isOne ) res ++ ; } // Repeat the above // process for right // to left direction. isOne = false ; for ( let j = C - 1 ; j >= 0 ; j -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } // Traversing across columns // for up and down directions. for ( let j = 0 ; j < C ; j ++ ) { // 1 is not seen yet let isOne = false ; for ( let i = 0 ; i < R ; i ++ ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } isOne = false ; for ( let i = R - 1 ; i >= 0 ; i -- ) { if ( mat [ i ][ j ] == 1 ) isOne = true ; else if ( isOne ) res ++ ; } } return res ; } let mat = [[ 0 0 0 0 ] [ 1 0 0 1 ] [ 0 1 1 0 ] [ 0 1 0 0 ]]; document . write ( getTotalCoverageOfMatrix ( mat )); < /script>
Wyjście
20
Złożoność czasowa: O(n 2 )
Przestrzeń pomocnicza: O(1)
Utwórz quiz