Warunek wstępny: Regresja liniowa

Regresja liniowa to algorytm uczenia maszynowego oparty na uczeniu nadzorowanym. Wykonuje zadanie regresji. Regresja modeluje docelową wartość przewidywaną w oparciu o zmienne niezależne. Stosowany jest głównie do ustalania związku między zmiennymi i prognozowania. Różne modele regresji różnią się w zależności od rodzaju relacji między zmiennymi zależnymi i niezależnymi, które uwzględniają, oraz liczby używanych zmiennych niezależnych. W tym artykule zademonstrujemy, jak używać różnych bibliotek Pythona do implementacji regresji liniowej na danym zbiorze danych. Zademonstrujemy binarny model liniowy, ponieważ będzie on łatwiejszy do wizualizacji. W tej demonstracji model będzie korzystał z metody gradientowej do nauki. Możesz się o tym dowiedzieć tutaj.

Krok 1: Importowanie wszystkich wymaganych bibliotek

Python3

import> numpy as np> import> pandas as pd> import> seaborn as sns> import> matplotlib.pyplot as plt> from> sklearn> import> preprocessing, svm> from> sklearn.model_selection> import> train_test_split> from> sklearn.linear_model> import> LinearRegression>

Krok 2: Odczytywanie zbioru danych:

Python3

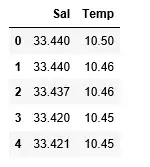
df> => pd.read_csv(> 'bottle.csv'> )> df_binary> => df[[> 'Salnty'> ,> 'T_degC'> ]]> > # Taking only the selected two attributes from the dataset> df_binary.columns> => [> 'Sal'> ,> 'Temp'> ]> #display the first 5 rows> df_binary.head()>

Wyjście:

Krok 3: Badanie rozproszenia danych

Python3

#plotting the Scatter plot to check relationship between Sal and Temp> sns.lmplot(x> => 'Sal'> , y> => 'Temp'> , data> => df_binary, order> => 2> , ci> => None> )> plt.show()>

Wyjście:

Krok 4: Czyszczenie danych

Python3

# Eliminating NaN or missing input numbers> df_binary.fillna(method> => 'ffill'> , inplace> => True> )>

Krok 5: Trening naszego modelu

Python3

X> => np.array(df_binary[> 'Sal'> ]).reshape(> -> 1> ,> 1> )> y> => np.array(df_binary[> 'Temp'> ]).reshape(> -> 1> ,> 1> )> > # Separating the data into independent and dependent variables> # Converting each dataframe into a numpy array> # since each dataframe contains only one column> df_binary.dropna(inplace> => True> )> > # Dropping any rows with Nan values> X_train, X_test, y_train, y_test> => train_test_split(X, y, test_size> => 0.25> )> > # Splitting the data into training and testing data> regr> => LinearRegression()> > regr.fit(X_train, y_train)> print> (regr.score(X_test, y_test))>

Wyjście:

Krok 6: Badanie naszych wyników

Python3

y_pred> => regr.predict(X_test)> plt.scatter(X_test, y_test, color> => 'b'> )> plt.plot(X_test, y_pred, color> => 'k'> )> > plt.show()> # Data scatter of predicted values>

Wyjście:

Niski wynik dokładności naszego modelu sugeruje, że nasz model regresyjny nie pasuje zbyt dobrze do istniejących danych. Sugeruje to, że nasze dane nie nadają się do regresji liniowej. Czasami jednak zbiór danych może zaakceptować regresor liniowy, jeśli weźmiemy pod uwagę tylko jego część. Sprawdźmy taką możliwość.

Krok 7: Praca z mniejszym zbiorem danych

Python3

df_binary500> => df_binary[:][:> 500> ]> > # Selecting the 1st 500 rows of the data> sns.lmplot(x> => 'Sal'> , y> => 'Temp'> , data> => df_binary500,> > order> => 2> , ci> => None> )>

Wyjście:

Widzimy już, że pierwsze 500 wierszy ma model liniowy. Kontynuując te same kroki, co poprzednio.

Python3

df_binary500.fillna(method> => 'fill'> , inplace> => True> )> > X> => np.array(df_binary500[> 'Sal'> ]).reshape(> -> 1> ,> 1> )> y> => np.array(df_binary500[> 'Temp'> ]).reshape(> -> 1> ,> 1> )> > df_binary500.dropna(inplace> => True> )> X_train, X_test, y_train, y_test> => train_test_split(X, y, test_size> => 0.25> )> > regr> => LinearRegression()> regr.fit(X_train, y_train)> print> (regr.score(X_test, y_test))>

Wyjście:

Python3

y_pred> => regr.predict(X_test)> plt.scatter(X_test, y_test, color> => 'b'> )> plt.plot(X_test, y_pred, color> => 'k'> )> > plt.show()>

Wyjście:

Krok 8: Metryki oceny dla regresji

Na koniec sprawdzamy wydajność modelu regresji liniowej za pomocą metryk ewaluacyjnych. W przypadku algorytmów regresji powszechnie używamy metryk mean_absolute_error i mean_squared_error w celu sprawdzenia wydajności modelu.

Python3

from> sklearn.metrics> import> mean_absolute_error,mean_squared_error> > mae> => mean_absolute_error(y_true> => y_test,y_pred> => y_pred)> #squared True returns MSE value, False returns RMSE value.> mse> => mean_squared_error(y_true> => y_test,y_pred> => y_pred)> #default=True> rmse> => mean_squared_error(y_true> => y_test,y_pred> => y_pred,squared> => False> )> > print> (> 'MAE:'> ,mae)> print> (> 'MSE:'> ,mse)> print> (> 'RMSE:'> ,rmse)>

Wyjście:

MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078