Struktury danych to sposób organizowania danych w taki sposób, aby można było do nich uzyskać bardziej efektywny dostęp w zależności od sytuacji. Struktury danych są podstawą każdego języka programowania, wokół którego budowany jest program. Python pomaga nauczyć się podstaw tych struktur danych w prostszy sposób w porównaniu do innych języków programowania.

W tym artykule omówimy struktury danych w języku programowania Python i ich powiązanie z niektórymi konkretnymi wbudowanymi strukturami danych, takimi jak krotki list, słowniki itp., a także niektórymi zaawansowanymi strukturami danych, takimi jak drzewa, wykresy itp.

Listy

Listy Pythona działają podobnie jak tablice, zadeklarowane w innych językach i stanowią uporządkowany zbiór danych. Jest bardzo elastyczny, ponieważ pozycje na liście nie muszą być tego samego typu.

Implementacja Python List jest podobna do Vectors w C++ lub ArrayList w JAVA. Kosztowną operacją jest wstawienie lub usunięcie elementu z początku Listy, gdyż konieczne jest przesunięcie wszystkich elementów. Wstawianie i usuwanie na końcu listy może być również kosztowne w przypadku zapełnienia wcześniej przydzielonej pamięci.

Możemy utworzyć listę w Pythonie, jak pokazano poniżej.

Przykład: tworzenie listy Pythona

Python3

List> => [> 1> ,> 2> ,> 3> ,> 'GFG'> ,> 2.3> ]> print> (> List> )>

Wyjście

[1, 2, 3, 'GFG', 2.3] 

Dostęp do elementów listy można uzyskać poprzez przypisany indeks. W indeksie początkowym listy w Pythonie sekwencja wynosi 0, a indeks końcowy to (jeśli jest tam N elementów) N-1.

Przykład: operacje na listach w Pythonie

Python3

# Creating a List with> # the use of multiple values> List> => [> 'Geeks'> ,> 'For'> ,> 'Geeks'> ]> print> (> ' List containing multiple values: '> )> print> (> List> )> # Creating a Multi-Dimensional List> # (By Nesting a list inside a List)> List2> => [[> 'Geeks'> ,> 'For'> ], [> 'Geeks'> ]]> print> (> ' Multi-Dimensional List: '> )> print> (List2)> # accessing a element from the> # list using index number> print> (> 'Accessing element from the list'> )> print> (> List> [> 0> ])> print> (> List> [> 2> ])> # accessing a element using> # negative indexing> print> (> 'Accessing element using negative indexing'> )> > # print the last element of list> print> (> List> [> -> 1> ])> > # print the third last element of list> print> (> List> [> -> 3> ])>

Wyjście

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks 

Słownik

Słownik Pythona jest jak tablice mieszające w dowolnym innym języku ze złożonością czasową O(1). Jest to nieuporządkowany zbiór wartości danych, używany do przechowywania wartości danych jak mapa, który w przeciwieństwie do innych typów danych, które przechowują tylko jedną wartość jako element, Słownik przechowuje parę klucz:wartość. W słowniku dostępna jest wartość klucz-wartość, aby była bardziej zoptymalizowana.

Indeksowanie słownika Pythona odbywa się za pomocą kluczy. Są to dowolne typy haszujące, tj. obiekty, których nigdy nie można zmieniać, jak ciągi znaków, liczby, krotki itp. Słownik możemy utworzyć za pomocą nawiasów klamrowych ({}) lub zrozumienie słownika .

Przykład: operacje słownikowe w Pythonie

Python3

# Creating a Dictionary> Dict> => {> 'Name'> :> 'Geeks'> ,> 1> : [> 1> ,> 2> ,> 3> ,> 4> ]}> print> (> 'Creating Dictionary: '> )> print> (> Dict> )> # accessing a element using key> print> (> 'Accessing a element using key:'> )> print> (> Dict> [> 'Name'> ])> # accessing a element using get()> # method> print> (> 'Accessing a element using get:'> )> print> (> Dict> .get(> 1> ))> # creation using Dictionary comprehension> myDict> => {x: x> *> *> 2> for> x> in> [> 1> ,> 2> ,> 3> ,> 4> ,> 5> ]}> print> (myDict)>

Wyjście

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} 

Krotka

Krotka Pythona to zbiór obiektów Pythona, podobny do listy, ale krotki są z natury niezmienne, tj. elementów krotki nie można dodawać ani usuwać po utworzeniu. Podobnie jak lista, krotka może również zawierać elementy różnych typów.

W Pythonie krotki tworzy się poprzez umieszczenie sekwencji wartości oddzielonych „przecinkiem” z użyciem nawiasów lub bez nich w celu grupowania sekwencji danych.

Notatka: Krotki można również tworzyć za pomocą pojedynczego elementu, ale jest to nieco trudne. Posiadanie jednego elementu w nawiasach nie wystarczy; musi znajdować się na końcu „przecinek”, aby był to krotka.

Przykład: operacje na krotkach w Pythonie

Python3

# Creating a Tuple with> # the use of Strings> Tuple> => (> 'Geeks'> ,> 'For'> )> print> (> ' Tuple with the use of String: '> )> print> (> Tuple> )> > # Creating a Tuple with> # the use of list> list1> => [> 1> ,> 2> ,> 4> ,> 5> ,> 6> ]> print> (> ' Tuple using List: '> )> Tuple> => tuple> (list1)> # Accessing element using indexing> print> (> 'First element of tuple'> )> print> (> Tuple> [> 0> ])> # Accessing element from last> # negative indexing> print> (> ' Last element of tuple'> )> print> (> Tuple> [> -> 1> ])> > print> (> ' Third last element of tuple'> )> print> (> Tuple> [> -> 3> ])>

Wyjście

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 

Ustawić

Zestaw Pythona to nieuporządkowany zbiór danych, który jest modyfikowalny i nie pozwala na duplikację elementu. Zestawy są zasadniczo używane do testowania członkostwa i eliminowania duplikatów wpisów. Wykorzystana w tym struktura danych to Hashing, popularna technika wykonywania wstawiania, usuwania i przeglądania średnio w O(1).

Jeśli na tej samej pozycji indeksu znajduje się wiele wartości, wówczas wartość jest dodawana do tej pozycji indeksu, tworząc listę połączoną. W tym zestawie zestawy CPython są implementowane przy użyciu słownika ze zmiennymi fikcyjnymi, w których kluczowe elementy są ustawiane przez członków z większymi optymalizacjami pod kątem złożoności czasowej.

Implementacja zestawu:

Zestawy z wieloma operacjami na pojedynczej tabeli HashTable:

Przykład: operacje na zestawach w Pythonie

Python3

# Creating a Set with> # a mixed type of values> # (Having numbers and strings)> Set> => set> ([> 1> ,> 2> ,> 'Geeks'> ,> 4> ,> 'For'> ,> 6> ,> 'Geeks'> ])> print> (> ' Set with the use of Mixed Values'> )> print> (> Set> )> # Accessing element using> # for loop> print> (> ' Elements of set: '> )> for> i> in> Set> :> > print> (i, end> => ' '> )> print> ()> # Checking the element> # using in keyword> print> (> 'Geeks'> in> Set> )>

Wyjście

Set with the use of Mixed Values {1, 2, 'Geeks', 4, 6, 'For'} Elements of set: 1 2 Geeks 4 6 For True 

Zamrożone zestawy

Zamrożone zbiory w Pythonie to niezmienne obiekty, które obsługują jedynie metody i operatory generujące wynik bez wpływu na zamrożony zbiór lub zestawy, do których są stosowane. Chociaż elementy zestawu można modyfikować w dowolnym momencie, elementy zamrożonego zestawu pozostają takie same po utworzeniu.

Jeśli nie zostaną przekazane żadne parametry, zwraca pusty zestaw zamrożony.

Python3

# Same as {'a', 'b','c'}> normal_set> => set> ([> 'a'> ,> 'b'> ,> 'c'> ])> print> (> 'Normal Set'> )> print> (normal_set)> # A frozen set> frozen_set> => frozenset> ([> 'e'> ,> 'f'> ,> 'g'> ])> print> (> ' Frozen Set'> )> print> (frozen_set)> # Uncommenting below line would cause error as> # we are trying to add element to a frozen set> # frozen_set.add('h')>

Wyjście

Normal Set {'a', 'c', 'b'} Frozen Set frozenset({'g', 'e', 'f'}) 

Strunowy

Ciągi Pythona to tablice bajtów reprezentujących znaki Unicode. Mówiąc prościej, ciąg znaków jest niezmienną tablicą znaków. Python nie ma znakowego typu danych, pojedynczy znak to po prostu ciąg znaków o długości 1.

Notatka: Ponieważ ciągi znaków są niezmienne, modyfikacja ciągu spowoduje utworzenie nowej kopii.

Przykład: operacje na ciągach znaków w języku Python

Python3

String> => 'Welcome to GeeksForGeeks'> print> (> 'Creating String: '> )> print> (String)> > # Printing First character> print> (> ' First character of String is: '> )> print> (String[> 0> ])> > # Printing Last character> print> (> ' Last character of String is: '> )> print> (String[> -> 1> ])>

Wyjście

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s 

Bajtearray

Python Bytearray daje zmienną sekwencję liczb całkowitych z zakresu 0 <= x < 256.

Przykład: operacje na bajtarray w Pythonie

Python3

# Creating bytearray> a> => bytearray((> 12> ,> 8> ,> 25> ,> 2> ))> print> (> 'Creating Bytearray:'> )> print> (a)> # accessing elements> print> (> ' Accessing Elements:'> , a[> 1> ])> # modifying elements> a[> 1> ]> => 3> print> (> ' After Modifying:'> )> print> (a)> # Appending elements> a.append(> 30> )> print> (> ' After Adding Elements:'> )> print> (a)>

Wyjście

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e') 

Do tej pory badaliśmy wszystkie struktury danych wbudowane w rdzeń Pythona. Zanurzmy się teraz głębiej w Pythona i przyjrzyjmy się modułowi kolekcji, który udostępnia kontenery, które są przydatne w wielu przypadkach i zapewniają więcej funkcji niż funkcje zdefiniowane powyżej.

Moduł Kolekcje

Moduł kolekcji Pythona został wprowadzony w celu poprawy funkcjonalności wbudowanych typów danych. Zapewnia różne kontenery, przyjrzyjmy się szczegółowo każdemu z nich.

Liczniki

Licznik jest podklasą słownika. Służy do przechowywania liczby elementów w iterowalnym słowniku w formie nieuporządkowanego słownika, gdzie klucz reprezentuje element w iterowalnym, a wartość reprezentuje liczbę tego elementu w iterowalnym. Jest to odpowiednik zestawu lub zbioru innych języków.

Przykład: operacje licznikowe w Pythonie

Python3

from> collections> import> Counter> > # With sequence of items> print> (Counter([> 'B'> ,> 'B'> ,> 'A'> ,> 'B'> ,> 'C'> ,> 'A'> ,> 'B'> ,> 'B'> ,> 'A'> ,> 'C'> ]))> > # with dictionary> count> => Counter({> 'A'> :> 3> ,> 'B'> :> 5> ,> 'C'> :> 2> })> print> (count)> count.update([> 'A'> ,> 1> ])> print> (count)>

Wyjście

Counter({'B': 5, 'A': 3, 'C': 2}) Counter({'B': 5, 'A': 3, 'C': 2}) Counter({'B': 5, 'A': 4, 'C': 2, 1: 1}) 

ZamówiłemDict

Jakiś ZamówiłemDict jest także podklasą słownika, ale w odróżnieniu od słownika zapamiętuje kolejność wstawiania klawiszy.

Przykład: operacje OrderedDict w języku Python

Python3

from> collections> import> OrderedDict> print> (> 'Before deleting: '> )> od> => OrderedDict()> od[> 'a'> ]> => 1> od[> 'b'> ]> => 2> od[> 'c'> ]> => 3> od[> 'd'> ]> => 4> for> key, value> in> od.items():> > print> (key, value)> print> (> ' After deleting: '> )> od.pop(> 'c'> )> for> key, value> in> od.items():> > print> (key, value)> print> (> ' After re-inserting: '> )> od[> 'c'> ]> => 3> for> key, value> in> od.items():> > print> (key, value)>

Wyjście

Before deleting: a 1 b 2 c 3 d 4 After deleting: a 1 b 2 d 4 After re-inserting: a 1 b 2 d 4 c 3 

Domyślny dykt

Domyślny dykt służy do podania domyślnych wartości klucza, który nie istnieje i nigdy nie wywołuje błędu KeyError. Jego obiekty można inicjować metodą DefaultDict(), przekazując typ danych jako argument.

Notatka: default_factory to funkcja udostępniająca domyślną wartość utworzonego słownika. Jeśli ten parametr jest nieobecny, zgłaszany jest błąd KeyError.

Przykład: operacje DefaultDict w języku Python

Python3

from> collections> import> defaultdict> > # Defining the dict> d> => defaultdict(> int> )> > L> => [> 1> ,> 2> ,> 3> ,> 4> ,> 2> ,> 4> ,> 1> ,> 2> ]> > # Iterate through the list> # for keeping the count> for> i> in> L:> > > # The default value is 0> > # so there is no need to> > # enter the key first> > d[i]> +> => 1> > print> (d)>

Wyjście

defaultdict(, {1: 2, 2: 3, 3: 1, 4: 2}) 

Mapa Łańcucha

ChainMap hermetyzuje wiele słowników w jedną jednostkę i zwraca listę słowników. Gdy konieczne jest odnalezienie klucza, przeszukiwane są kolejno wszystkie słowniki, aż do znalezienia klucza.

Przykład: operacje na mapie łańcuchowej w języku Python

Python3

from> collections> import> ChainMap> > > d1> => {> 'a'> :> 1> ,> 'b'> :> 2> }> d2> => {> 'c'> :> 3> ,> 'd'> :> 4> }> d3> => {> 'e'> :> 5> ,> 'f'> :> 6> }> > # Defining the chainmap> c> => ChainMap(d1, d2, d3)> print> (c)> print> (c[> 'a'> ])> print> (c[> 'g'> ])>

Wyjście

ChainMap({'a': 1, 'b': 2}, {'c': 3, 'd': 4}, {'e': 5, 'f': 6}) 1 

KeyError: 'g' 

NazwanyTuple

A NazwanyTuple zwraca obiekt krotki z nazwami dla każdej pozycji, których brakuje zwykłym krotkom. Rozważmy na przykład krotkę nazw student, w której pierwszy element reprezentuje fname, drugi reprezentuje lname, a trzeci element reprezentuje DOB. Załóżmy, że zamiast zapamiętywać pozycję w indeksie, wywołując fname, możesz faktycznie wywołać element za pomocą argumentu fname, wtedy dostęp do elementu krotki będzie naprawdę łatwy. Ta funkcjonalność jest zapewniana przez NamedTuple.

Przykład: operacje NamedTuple w języku Python

Python3

from> collections> import> namedtuple> > # Declaring namedtuple()> Student> => namedtuple(> 'Student'> ,[> 'name'> ,> 'age'> ,> 'DOB'> ])> > # Adding values> S> => Student(> 'Nandini'> ,> '19'> ,> '2541997'> )> > # Access using index> print> (> 'The Student age using index is : '> ,end> => '')> print> (S[> 1> ])> > # Access using name> print> (> 'The Student name using keyname is : '> ,end> => '')> print> (S.name)>

Wyjście

The Student age using index is : 19 The Student name using keyname is : Nandini 

O czym

Deque (kolejka podwójnie zakończona) to zoptymalizowana lista umożliwiająca szybsze operacje dołączania i otwierania z obu stron kontenera. Zapewnia złożoność czasową O(1) dla operacji dołączania i otwierania w porównaniu z listą ze złożonością czasową O(n).

Python Deque jest zaimplementowany przy użyciu podwójnie połączonych list, dlatego wydajność losowego dostępu do elementów wynosi O(n).

Przykład: operacje Deque w Pythonie

Python3

# importing 'collections' for deque operations> import> collections> # initializing deque> de> => collections.deque([> 1> ,> 2> ,> 3> ])> # using append() to insert element at right end> # inserts 4 at the end of deque> de.append(> 4> )> # printing modified deque> print> (> 'The deque after appending at right is : '> )> print> (de)> # using appendleft() to insert element at left end> # inserts 6 at the beginning of deque> de.appendleft(> 6> )> # printing modified deque> print> (> 'The deque after appending at left is : '> )> print> (de)> # using pop() to delete element from right end> # deletes 4 from the right end of deque> de.pop()> # printing modified deque> print> (> 'The deque after deleting from right is : '> )> print> (de)> # using popleft() to delete element from left end> # deletes 6 from the left end of deque> de.popleft()> # printing modified deque> print> (> 'The deque after deleting from left is : '> )> print> (de)>

Wyjście

The deque after appending at right is : deque([1, 2, 3, 4]) The deque after appending at left is : deque([6, 1, 2, 3, 4]) The deque after deleting from right is : deque([6, 1, 2, 3]) The deque after deleting from left is : deque([1, 2, 3]) 

UserDict

UserDict to kontener przypominający słownik, który działa jak opakowanie wokół obiektów słownika. Kontener ten jest używany, gdy ktoś chce stworzyć własny słownik ze zmodyfikowanymi lub nowymi funkcjami.

Przykład: UserDict w Pythonie

Python3

from> collections> import> UserDict> # Creating a Dictionary where> # deletion is not allowed> class> MyDict(UserDict):> > > # Function to stop deletion> > # from dictionary> > def> __del__(> self> ):> > raise> RuntimeError(> 'Deletion not allowed'> )> > > # Function to stop pop from> > # dictionary> > def> pop(> self> , s> => None> ):> > raise> RuntimeError(> 'Deletion not allowed'> )> > > # Function to stop popitem> > # from Dictionary> > def> popitem(> self> , s> => None> ):> > raise> RuntimeError(> 'Deletion not allowed'> )> > # Driver's code> d> => MyDict({> 'a'> :> 1> ,> > 'b'> :> 2> ,> > 'c'> :> 3> })> print> (> 'Original Dictionary'> )> print> (d)> d.pop(> 1> )>

Wyjście

Original Dictionary {'a': 1, 'b': 2, 'c': 3} 

RuntimeError: Deletion not allowed 

Lista użytkowników

UserList to kontener przypominający listę, który pełni funkcję opakowania wokół obiektów listy. Jest to przydatne, gdy ktoś chce stworzyć własną listę ze zmodyfikowanymi lub dodatkowymi funkcjami.

Przykłady: Lista użytkowników Pythona

Python3

# Python program to demonstrate> # userlist> from> collections> import> UserList> # Creating a List where> # deletion is not allowed> class> MyList(UserList):> > > # Function to stop deletion> > # from List> > def> remove(> self> , s> => None> ):> > raise> RuntimeError(> 'Deletion not allowed'> )> > > # Function to stop pop from> > # List> > def> pop(> self> , s> => None> ):> > raise> RuntimeError(> 'Deletion not allowed'> )> > # Driver's code> L> => MyList([> 1> ,> 2> ,> 3> ,> 4> ])> print> (> 'Original List'> )> print> (L)> # Inserting to List'> L.append(> 5> )> print> (> 'After Insertion'> )> print> (L)> # Deleting From List> L.remove()>

Wyjście

Original List [1, 2, 3, 4] After Insertion [1, 2, 3, 4, 5] 

RuntimeError: Deletion not allowed 

Ciąg użytkownika

UserString jest kontenerem przypominającym ciąg znaków i podobnie jak UserDict i UserList działa jako opakowanie wokół obiektów łańcuchowych. Używa się go, gdy ktoś chce stworzyć własne ciągi znaków z pewnymi zmodyfikowanymi lub dodatkowymi funkcjonalnościami.

Przykład: ciąg użytkownika Pythona

Python3

from> collections> import> UserString> # Creating a Mutable String> class> Mystring(UserString):> > > # Function to append to> > # string> > def> append(> self> , s):> > self> .data> +> => s> > > # Function to remove from> > # string> > def> remove(> self> , s):> > self> .data> => self> .data.replace(s, '')> > # Driver's code> s1> => Mystring(> 'Geeks'> )> print> (> 'Original String:'> , s1.data)> # Appending to string> s1.append(> 's'> )> print> (> 'String After Appending:'> , s1.data)> # Removing from string> s1.remove(> 'e'> )> print> (> 'String after Removing:'> , s1.data)>

Wyjście

Original String: Geeks String After Appending: Geekss String after Removing: Gkss 

Teraz, po przestudiowaniu wszystkich struktur danych, przyjrzyjmy się zaawansowanym strukturom danych, takim jak stos, kolejka, wykres, lista połączona itp., których można używać w języku Python.

Połączona lista

Lista połączona to liniowa struktura danych, w której elementy nie są przechowywane w sąsiadujących lokalizacjach pamięci. Elementy na połączonej liście są połączone za pomocą wskaźników, jak pokazano na poniższym obrazku:

Połączona lista jest reprezentowana przez wskaźnik do pierwszego węzła połączonej listy. Pierwszy węzeł nazywany jest głową. Jeśli połączona lista jest pusta, wartość nagłówka wynosi NULL. Każdy węzeł na liście składa się z co najmniej dwóch części:

• Dane
• Wskaźnik (lub odniesienie) do następnego węzła

Przykład: definiowanie listy połączonej w Pythonie

Python3

# Node class> class> Node:> > # Function to initialize the node object> > def> __init__(> self> , data):> > self> .data> => data> # Assign data> > self> .> next> => None> # Initialize> > # next as null> # Linked List class> class> LinkedList:> > > # Function to initialize the Linked> > # List object> > def> __init__(> self> ):> > self> .head> => None>

Stwórzmy prostą listę połączoną z 3 węzłami.

Python3

# A simple Python program to introduce a linked list> # Node class> class> Node:> > # Function to initialise the node object> > def> __init__(> self> , data):> > self> .data> => data> # Assign data> > self> .> next> => None> # Initialize next as null> # Linked List class contains a Node object> class> LinkedList:> > # Function to initialize head> > def> __init__(> self> ):> > self> .head> => None> # Code execution starts here> if> __name__> => => '__main__'> :> > # Start with the empty list> > list> => LinkedList()> > list> .head> => Node(> 1> )> > second> => Node(> 2> )> > third> => Node(> 3> )> > '''> > Three nodes have been created.> > We have references to these three blocks as head,> > second and third> > list.head second third> > | | |> > | | |> > +----+------+ +----+------+ +----+------+> > | 1 | None | | 2 | None | | 3 | None |> > +----+------+ +----+------+ +----+------+> > '''> > list> .head.> next> => second;> # Link first node with second> > '''> > Now next of first Node refers to second. So they> > both are linked.> > list.head second third> > | | |> > | | |> > +----+------+ +----+------+ +----+------+> > | 1 | o-------->| 2 | zero | | 3 | null |> > +----+------+ +----+------+ +----+------+> > '''> > second.> next> => third;> # Link second node with the third node> > '''> > Now next of second Node refers to third. So all three> > nodes are linked.> > list.head second third> > | | |> > | | |> > +----+------+ +----+------+ +----+------+> > | 1 | o-------->| 2 | o-------->| 3 | null |> > +----+------+ +----+------+ +----+------+> > '''>

Przeglądanie połączonej listy

W poprzednim programie utworzyliśmy prostą listę połączoną z trzema węzłami. Przejdźmy przez utworzoną listę i wydrukujmy dane każdego węzła. Na potrzeby przechodzenia napiszmy uniwersalną funkcję printList(), która wypisuje dowolną listę.

Python3

# A simple Python program for traversal of a linked list> # Node class> class> Node:> > # Function to initialise the node object> > def> __init__(> self> , data):> > self> .data> => data> # Assign data> > self> .> next> => None> # Initialize next as null> # Linked List class contains a Node object> class> LinkedList:> > # Function to initialize head> > def> __init__(> self> ):> > self> .head> => None> > # This function prints contents of linked list> > # starting from head> > def> printList(> self> ):> > temp> => self> .head> > while> (temp):> > print> (temp.data)> > temp> => temp.> next> # Code execution starts here> if> __name__> => => '__main__'> :> > # Start with the empty list> > list> => LinkedList()> > list> .head> => Node(> 1> )> > second> => Node(> 2> )> > third> => Node(> 3> )> > list> .head.> next> => second;> # Link first node with second> > second.> next> => third;> # Link second node with the third node> > list> .printList()>

Wyjście

1 2 3 

Stos

A stos to liniowa struktura danych, która przechowuje elementy w sposób „ostatnie weszło/pierwsze wyszło” (LIFO) lub „pierwsze weszło/ostatni wyszło” (FILO). W stosie nowy element jest dodawany na jednym końcu, a element jest usuwany tylko z tego końca. Operacje wstawiania i usuwania są często nazywane push i pop.

Funkcje powiązane ze stosem to:

pusty() – Zwraca, czy stos jest pusty – Złożoność czasowa: O(1) size() – Zwraca rozmiar stosu – Złożoność czasowa: O(1) top() – Zwraca referencję do najwyższego elementu stosu – Złożoność czasowa: O(1) push(a) – Wstawia element „a” na szczyt stosu – Złożoność czasowa: O(1) pop() – Usuwa najwyższy element stosu – Złożoność czasowa: O( 1)

Implementacja stosu Pythona

Stos w Pythonie można zaimplementować na następujące sposoby:

• lista
• Kolekcje.deque
• kolejka.LifoQueue

Implementacja przy użyciu listy

Wbudowanej w Pythona listy struktur danych można używać jako stosu. Zamiast push() append() służy do dodawania elementów na górę stosu, podczas gdy pop() usuwa element w kolejności LIFO.

Python3

stack> => []> # append() function to push> # element in the stack> stack.append(> 'g'> )> stack.append(> 'f'> )> stack.append(> 'g'> )> print> (> 'Initial stack'> )> print> (stack)> # pop() function to pop> # element from stack in> # LIFO order> print> (> ' Elements popped from stack:'> )> print> (stack.pop())> print> (stack.pop())> print> (stack.pop())> print> (> ' Stack after elements are popped:'> )> print> (stack)> # uncommenting print(stack.pop())> # will cause an IndexError> # as the stack is now empty>

Wyjście

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: [] 

Implementacja przy użyciu Collections.deque:

Stos Pythona można zaimplementować przy użyciu klasy deque z modułu kolekcji. Deque jest preferowany zamiast listy w przypadkach, gdy potrzebujemy szybszych operacji dołączania i pop z obu końców kontenera, ponieważ deque zapewnia złożoność czasową O(1) dla operacji dołączania i pop w porównaniu z listą, która zapewnia O(n) złożoność czasu.

Python3

from> collections> import> deque> stack> => deque()> # append() function to push> # element in the stack> stack.append(> 'g'> )> stack.append(> 'f'> )> stack.append(> 'g'> )> print> (> 'Initial stack:'> )> print> (stack)> # pop() function to pop> # element from stack in> # LIFO order> print> (> ' Elements popped from stack:'> )> print> (stack.pop())> print> (stack.pop())> print> (stack.pop())> print> (> ' Stack after elements are popped:'> )> print> (stack)> # uncommenting print(stack.pop())> # will cause an IndexError> # as the stack is now empty>

Wyjście

Initial stack: deque(['g', 'f', 'g']) Elements popped from stack: g f g Stack after elements are popped: deque([]) 

Implementacja z wykorzystaniem modułu kolejkowego

Moduł kolejki ma również kolejkę LIFO, która jest w zasadzie stosem. Dane są wstawiane do kolejki za pomocą funkcji put(), a funkcja get() pobiera dane z kolejki.

Python3

from> queue> import> LifoQueue> # Initializing a stack> stack> => LifoQueue(maxsize> => 3> )> # qsize() show the number of elements> # in the stack> print> (stack.qsize())> # put() function to push> # element in the stack> stack.put(> 'g'> )> stack.put(> 'f'> )> stack.put(> 'g'> )> print> (> 'Full: '> , stack.full())> print> (> 'Size: '> , stack.qsize())> # get() function to pop> # element from stack in> # LIFO order> print> (> ' Elements popped from the stack'> )> print> (stack.get())> print> (stack.get())> print> (stack.get())> print> (> ' Empty: '> , stack.empty())>

Wyjście

0 Full: True Size: 3 Elements popped from the stack g f g Empty: True 

Kolejka

Jako stos, kolejka to liniowa struktura danych, w której przechowywane są pozycje według zasady „pierwsze weszło, pierwsze wyszło” (FIFO). W przypadku kolejki ostatnio dodany element jest usuwany jako pierwszy. Dobrym przykładem kolejki jest dowolna kolejka konsumentów do zasobu, w której konsument, który przyszedł pierwszy, jest obsługiwany jako pierwszy.

Operacje związane z kolejką to:

Kolejkuj: Dodaje element do kolejki. Jeśli kolejka jest pełna, mówimy o stanie przepełnienia – Złożoność czasowa: O(1) Usuń z kolejki: Usuwa element z kolejki. Elementy są wysuwane w tej samej kolejności, w jakiej są wypychane. Jeśli kolejka jest pusta, mówi się, że jest to warunek niedopełnienia – Złożoność czasu: O(1) Przód: Pobierz element z przodu z kolejki – Złożoność czasu: O(1) Tył: Pobierz ostatni element z kolejki – Złożoność czasu : O(1)

Implementacja kolejki w Pythonie

Kolejkę w Pythonie można zaimplementować na następujące sposoby:

• lista
• kolekcje.deque
• ogon.ogon

Implementacja za pomocą listy

Zamiast enqueue() i dequeue() używana jest funkcja append() i pop().

Python3

# Initializing a queue> queue> => []> # Adding elements to the queue> queue.append(> 'g'> )> queue.append(> 'f'> )> queue.append(> 'g'> )> print> (> 'Initial queue'> )> print> (queue)> # Removing elements from the queue> print> (> ' Elements dequeued from queue'> )> print> (queue.pop(> 0> ))> print> (queue.pop(> 0> ))> print> (queue.pop(> 0> ))> print> (> ' Queue after removing elements'> )> print> (queue)> # Uncommenting print(queue.pop(0))> # will raise and IndexError> # as the queue is now empty>

Wyjście

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements [] 

Implementacja przy użyciu Collections.deque

Deque jest preferowany zamiast listy w przypadkach, gdy potrzebujemy szybszych operacji dołączania i pop z obu końców kontenera, ponieważ deque zapewnia złożoność czasową O(1) dla operacji dołączania i pop w porównaniu z listą, która zapewnia O(n) złożoność czasu.

Python3

from> collections> import> deque> # Initializing a queue> q> => deque()> # Adding elements to a queue> q.append(> 'g'> )> q.append(> 'f'> )> q.append(> 'g'> )> print> (> 'Initial queue'> )> print> (q)> # Removing elements from a queue> print> (> ' Elements dequeued from the queue'> )> print> (q.popleft())> print> (q.popleft())> print> (q.popleft())> print> (> ' Queue after removing elements'> )> print> (q)> # Uncommenting q.popleft()> # will raise an IndexError> # as queue is now empty>

Wyjście

Initial queue deque(['g', 'f', 'g']) Elements dequeued from the queue g f g Queue after removing elements deque([]) 

Implementacja z wykorzystaniem kolejki.Kolejka

kolejka.Queue(maxsize) inicjuje zmienną do maksymalnego rozmiaru maxsize. Maksymalny rozmiar wynoszący zero „0” oznacza nieskończoną kolejkę. Ta kolejka jest zgodna z regułą FIFO.

Python3

from> queue> import> Queue> # Initializing a queue> q> => Queue(maxsize> => 3> )> # qsize() give the maxsize> # of the Queue> print> (q.qsize())> # Adding of element to queue> q.put(> 'g'> )> q.put(> 'f'> )> q.put(> 'g'> )> # Return Boolean for Full> # Queue> print> (> ' Full: '> , q.full())> # Removing element from queue> print> (> ' Elements dequeued from the queue'> )> print> (q.get())> print> (q.get())> print> (q.get())> # Return Boolean for Empty> # Queue> print> (> ' Empty: '> , q.empty())> q.put(> 1> )> print> (> ' Empty: '> , q.empty())> print> (> 'Full: '> , q.full())> # This would result into Infinite> # Loop as the Queue is empty.> # print(q.get())>

Wyjście

0 Full: True Elements dequeued from the queue g f g Empty: True Empty: False Full: False 

Kolejka priorytetowa

Kolejki priorytetowe to abstrakcyjne struktury danych, w których każde dane/wartość w kolejce mają określony priorytet. Na przykład w liniach lotniczych bagaż z tytułem Biznes lub Pierwsza klasa przybywa wcześniej niż reszta. Kolejka priorytetowa jest rozszerzeniem kolejki o następujących właściwościach.

• Element o wysokim priorytecie jest usuwany z kolejki przed elementem o niskim priorytecie.
• Jeżeli dwa elementy mają ten sam priorytet, są obsługiwane zgodnie z kolejnością w kolejce.

Python3

# A simple implementation of Priority Queue> # using Queue.> class> PriorityQueue(> object> ):> > def> __init__(> self> ):> > self> .queue> => []> > def> __str__(> self> ):> > return> ' '> .join([> str> (i)> for> i> in> self> .queue])> > # for checking if the queue is empty> > def> isEmpty(> self> ):> > return> len> (> self> .queue)> => => 0> > # for inserting an element in the queue> > def> insert(> self> , data):> > self> .queue.append(data)> > # for popping an element based on Priority> > def> delete(> self> ):> > try> :> > max> => 0> > for> i> in> range> (> len> (> self> .queue)):> > if> self> .queue[i]>> self> .queue[> max> ]:> > max> => i> > item> => self> .queue[> max> ]> > del> self> .queue[> max> ]> > return> item> > except> IndexError:> > print> ()> > exit()> if> __name__> => => '__main__'> :> > myQueue> => PriorityQueue()> > myQueue.insert(> 12> )> > myQueue.insert(> 1> )> > myQueue.insert(> 14> )> > myQueue.insert(> 7> )> > print> (myQueue)> > while> not> myQueue.isEmpty():> > print> (myQueue.delete())>

Wyjście

12 1 14 7 14 12 7 1 

Kolejka sterty (lub sterta)

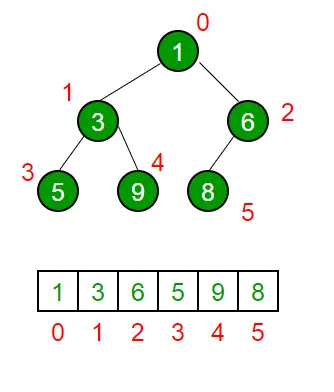
moduł sterty w Pythonie zapewnia strukturę danych sterty, która jest używana głównie do reprezentowania kolejki priorytetowej. Właściwość tej struktury danych w Pythonie polega na tym, że za każdym razem, gdy pojawia się najmniejszy element sterty (min-heap). Za każdym razem, gdy elementy są wypychane lub otwierane, struktura sterty zostaje zachowana. Element sterty[0] również zwraca za każdym razem najmniejszy element.

Obsługuje ekstrakcję i wstawianie najmniejszego elementu w czasach O (log n).

Python3

# importing 'heapq' to implement heap queue> import> heapq> # initializing list> li> => [> 5> ,> 7> ,> 9> ,> 1> ,> 3> ]> # using heapify to convert list into heap> heapq.heapify(li)> # printing created heap> print> (> 'The created heap is : '> ,end> => '')> print> (> list> (li))> # using heappush() to push elements into heap> # pushes 4> heapq.heappush(li,> 4> )> # printing modified heap> print> (> 'The modified heap after push is : '> ,end> => '')> print> (> list> (li))> # using heappop() to pop smallest element> print> (> 'The popped and smallest element is : '> ,end> => '')> print> (heapq.heappop(li))>

Wyjście

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1 

Drzewo binarne

Drzewo to hierarchiczna struktura danych, która wygląda jak na poniższym rysunku –

 tree ---- j  <-- root /  f k /   a h z  <-- leaves 

Najwyższy węzeł drzewa nazywany jest korzeniem, natomiast węzły położone najniżej lub węzły nieposiadające dzieci nazywane są węzłami liściowymi. Węzły znajdujące się bezpośrednio pod węzłem nazywane są jego dziećmi, a węzły znajdujące się bezpośrednio nad czymś nazywane są jego rodzicami.

Drzewo binarne to drzewo, którego elementy mogą mieć prawie dwoje dzieci. Ponieważ każdy element drzewa binarnego może mieć tylko 2 dzieci, zazwyczaj nazywamy je lewym i prawym dzieckiem. Węzeł drzewa binarnego zawiera następujące części.

• Dane
• Wskaźnik do lewego dziecka
• Wskaźnik do odpowiedniego dziecka

Przykład: definiowanie klasy węzła

Python3

# A Python class that represents an individual node> # in a Binary Tree> class> Node:> > def> __init__(> self> ,key):> > self> .left> => None> > self> .right> => None> > self> .val> => key>

Stwórzmy teraz drzewo z 4 węzłami w Pythonie. Załóżmy, że struktura drzewa wygląda jak poniżej –

 tree ---- 1  <-- root /  2 3 / 4 

Przykład: Dodawanie danych do drzewa

Python3

# Python program to introduce Binary Tree> # A class that represents an individual node in a> # Binary Tree> class> Node:> > def> __init__(> self> ,key):> > self> .left> => None> > self> .right> => None> > self> .val> => key> # create root> root> => Node(> 1> )> ''' following is the tree after above statement> > 1> > /> > None None'''> root.left> => Node(> 2> );> root.right> => Node(> 3> );> ''' 2 and 3 become left and right children of 1> > 1> > /> > 2 3> > / /> None None None None'''> root.left.left> => Node(> 4> );> '''4 becomes left child of 2> > 1> > /> > 2 3> > / /> 4 None None None> /> None None'''>

Przejście przez drzewo

Drzewa można przemierzać na różne sposoby. Poniżej przedstawiono ogólnie stosowane sposoby przechodzenia przez drzewa. Rozważmy poniższe drzewo –

 tree ---- 1  <-- root /  2 3 /  4 5 

Pierwsze przejścia na głębokość:

• Inorder (lewy, główny, prawy): 4 2 5 1 3
• Zamawianie w przedsprzedaży (główny, lewy, prawy): 1 2 4 5 3
• Postorder (lewy, prawy, główny): 4 5 2 3 1

Algorytm Inorder(drzewo)

• Przejdź przez lewe poddrzewo, tj. wywołaj Inorder(lewe poddrzewo)
• Odwiedź korzeń.
• Przejdź przez prawe poddrzewo, tj. wywołaj Inorder(prawe poddrzewo)

Algorytm w przedsprzedaży (drzewo)

• Odwiedź korzeń.
• Przejdź przez lewe poddrzewo, tj. wywołaj Preorder(lewe poddrzewo)
• Przejdź przez prawe poddrzewo, tj. wywołaj Preorder(prawe poddrzewo)

Algorytm Przekaz pocztowy (drzewo)

• Przejdź przez lewe poddrzewo, tj. wywołaj Postorder(lewe poddrzewo)
• Przejdź przez prawe poddrzewo, tj. wywołaj Postorder(prawe poddrzewo)
• Odwiedź korzeń.

Python3

# Python program to for tree traversals> # A class that represents an individual node in a> # Binary Tree> class> Node:> > def> __init__(> self> , key):> > self> .left> => None> > self> .right> => None> > self> .val> => key> # A function to do inorder tree traversal> def> printInorder(root):> > if> root:> > # First recur on left child> > printInorder(root.left)> > # then print the data of node> > print> (root.val),> > # now recur on right child> > printInorder(root.right)> # A function to do postorder tree traversal> def> printPostorder(root):> > if> root:> > # First recur on left child> > printPostorder(root.left)> > # the recur on right child> > printPostorder(root.right)> > # now print the data of node> > print> (root.val),> # A function to do preorder tree traversal> def> printPreorder(root):> > if> root:> > # First print the data of node> > print> (root.val),> > # Then recur on left child> > printPreorder(root.left)> > # Finally recur on right child> > printPreorder(root.right)> # Driver code> root> => Node(> 1> )> root.left> => Node(> 2> )> root.right> => Node(> 3> )> root.left.left> => Node(> 4> )> root.left.right> => Node(> 5> )> print> (> 'Preorder traversal of binary tree is'> )> printPreorder(root)> print> (> ' Inorder traversal of binary tree is'> )> printInorder(root)> print> (> ' Postorder traversal of binary tree is'> )> printPostorder(root)>

Wyjście

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1 

Złożoność czasowa – O(n)

Przechodzenie według szerokości lub kolejności poziomów

Przechodzenie przez poziom drzewa oznacza przejście drzewa wszerz. Kolejność poziomów w powyższym drzewie wynosi 1 2 3 4 5.

Dla każdego węzła najpierw odwiedzany jest węzeł, a następnie jego węzły podrzędne umieszczane są w kolejce FIFO. Poniżej znajduje się algorytm dla tego samego -

• Utwórz pustą kolejkę q
• temp_node = root /*zacznij od katalogu głównego*/
• Zapętlaj, gdy temp_node nie ma wartości NULL
  • wydrukuj węzeł temp_>dane.
  • Umieść w kolejce dzieci temp_node (najpierw lewe, potem prawe) do q
  • Usuń z kolejki węzeł z q

Python3

# Python program to print level> # order traversal using Queue> # A node structure> class> Node:> > > # A utility function to create a new node> > def> __init__(> self> ,key):> > self> .data> => key> > self> .left> => None> > self> .right> => None> # Iterative Method to print the> # height of a binary tree> def> printLevelOrder(root):> > > # Base Case> > if> root> is> None> :> > return> > > # Create an empty queue> > # for level order traversal> > queue> => []> > # Enqueue Root and initialize height> > queue.append(root)> > while> (> len> (queue)>> 0> ):> > > # Print front of queue and> > # remove it from queue> > print> (queue[> 0> ].data)> > node> => queue.pop(> 0> )> > # Enqueue left child> > if> node.left> is> not> None> :> > queue.append(node.left)> > # Enqueue right child> > if> node.right> is> not> None> :> > queue.append(node.right)> # Driver Program to test above function> root> => Node(> 1> )> root.left> => Node(> 2> )> root.right> => Node(> 3> )> root.left.left> => Node(> 4> )> root.left.right> => Node(> 5> )> print> (> 'Level Order Traversal of binary tree is -'> )> printLevelOrder(root)>

Wyjście

Level Order Traversal of binary tree is - 1 2 3 4 5 

Złożoność czasowa: O(n)

Wykres

A wykres jest nieliniową strukturą danych składającą się z węzłów i krawędzi. Węzły są czasami nazywane także wierzchołkami, a krawędzie to linie lub łuki łączące dowolne dwa węzły na wykresie. Bardziej formalnie graf można zdefiniować jako graf składający się ze skończonego zestawu wierzchołków (lub węzłów) i zestawu krawędzi łączących parę węzłów.

Na powyższym Grafice zbiór wierzchołków V = {0,1,2,3,4} i zbiór krawędzi E = {01, 12, 23, 34, 04, 14, 13}.

Poniższe dwie są najczęściej używanymi reprezentacjami wykresu.

• Macierz sąsiedztwa
• Lista sąsiedztwa

Macierz sąsiedztwa

Macierz sąsiedztwa to tablica 2D o wymiarach V x V, gdzie V to liczba wierzchołków grafu. Niech tablicą 2D będzie adj[][], szczelina adj[i][j] = 1 wskazuje, że istnieje krawędź od wierzchołka i do wierzchołka j. Macierz sąsiedztwa dla grafu nieskierowanego jest zawsze symetryczna. Macierz przylegania jest również używana do reprezentowania wykresów ważonych. Jeśli adj[i][j] = w, to istnieje krawędź od wierzchołka i do wierzchołka j o wadze w.

Python3

# A simple representation of graph using Adjacency Matrix> class> Graph:> > def> __init__(> self> ,numvertex):> > self> .adjMatrix> => [[> -> 1> ]> *> numvertex> for> x> in> range> (numvertex)]> > self> .numvertex> => numvertex> > self> .vertices> => {}> > self> .verticeslist> => [> 0> ]> *> numvertex> > def> set_vertex(> self> ,vtx,> id> ):> > if> 0> <> => vtx <> => self> .numvertex:> > self> .vertices[> id> ]> => vtx> > self> .verticeslist[vtx]> => id> > def> set_edge(> self> ,frm,to,cost> => 0> ):> > frm> => self> .vertices[frm]> > to> => self> .vertices[to]> > self> .adjMatrix[frm][to]> => cost> > > # for directed graph do not add this> > self> .adjMatrix[to][frm]> => cost> > def> get_vertex(> self> ):> > return> self> .verticeslist> > def> get_edges(> self> ):> > edges> => []> > for> i> in> range> (> self> .numvertex):> > for> j> in> range> (> self> .numvertex):> > if> (> self> .adjMatrix[i][j]!> => -> 1> ):> > edges.append((> self> .verticeslist[i],> self> .verticeslist[j],> self> .adjMatrix[i][j]))> > return> edges> > > def> get_matrix(> self> ):> > return> self> .adjMatrix> G> => Graph(> 6> )> G.set_vertex(> 0> ,> 'a'> )> G.set_vertex(> 1> ,> 'b'> )> G.set_vertex(> 2> ,> 'c'> )> G.set_vertex(> 3> ,> 'd'> )> G.set_vertex(> 4> ,> 'e'> )> G.set_vertex(> 5> ,> 'f'> )> G.set_edge(> 'a'> ,> 'e'> ,> 10> )> G.set_edge(> 'a'> ,> 'c'> ,> 20> )> G.set_edge(> 'c'> ,> 'b'> ,> 30> )> G.set_edge(> 'b'> ,> 'e'> ,> 40> )> G.set_edge(> 'e'> ,> 'd'> ,> 50> )> G.set_edge(> 'f'> ,> 'e'> ,> 60> )> print> (> 'Vertices of Graph'> )> print> (G.get_vertex())> print> (> 'Edges of Graph'> )> print> (G.get_edges())> print> (> 'Adjacency Matrix of Graph'> )> print> (G.get_matrix())>

Wyjście

Wierzchołki grafu

['Alfabet']

Krawędzie wykresu

[('a', 'c', 20), ('a', 'e', ​​10), ('b', 'c', 30), ('b', 'e', ​​40), ( „c”, „a”, 20), („c”, „b”, 30), („d”, „e”, 50), („e”, „a”, 10), („e ', 'b', 40), ('e', 'd', 50), ('e', 'f', 60), ('f', 'e', ​​60)]

Macierz sąsiedztwa grafu

[[-1, -1, 20, -1, 10, -1], [-1, -1, 30, -1, 40, -1], [20, 30, -1, -1, -1 , -1], [-1, -1, -1, -1, 50, -1], [10, 40, -1, 50, -1, 60], [-1, -1, -1, -1, 60, -1]]

Lista sąsiedztwa

Używana jest tablica list. Rozmiar tablicy jest równy liczbie wierzchołków. Niech tablica będzie tablicą[]. Tablica wpisów[i] reprezentuje listę wierzchołków sąsiadujących z i-tym wierzchołkiem. Reprezentację tę można również wykorzystać do przedstawienia wykresu ważonego. Wagi krawędzi można przedstawić w postaci list par. Poniżej znajduje się lista sąsiedztwa powyższego wykresu.

Python3

# A class to represent the adjacency list of the node> class> AdjNode:> > def> __init__(> self> , data):> > self> .vertex> => data> > self> .> next> => None> # A class to represent a graph. A graph> # is the list of the adjacency lists.> # Size of the array will be the no. of the> # vertices 'V'> class> Graph:> > def> __init__(> self> , vertices):> > self> .V> => vertices> > self> .graph> => [> None> ]> *> self> .V> > # Function to add an edge in an undirected graph> > def> add_edge(> self> , src, dest):> > > # Adding the node to the source node> > node> => AdjNode(dest)> > node.> next> => self> .graph[src]> > self> .graph[src]> => node> > # Adding the source node to the destination as> > # it is the undirected graph> > node> => AdjNode(src)> > node.> next> => self> .graph[dest]> > self> .graph[dest]> => node> > # Function to print the graph> > def> print_graph(> self> ):> > for> i> in> range> (> self> .V):> > print> (> 'Adjacency list of vertex {} head'> .> format> (i), end> => '')> > temp> => self> .graph[i]> > while> temp:> > print> (> ' ->{}'> .> format> (temp.vertex), end> => '')> > temp> => temp.> next> > print> (> ' '> )> # Driver program to the above graph class> if> __name__> => => '__main__'> :> > V> => 5> > graph> => Graph(V)> > graph.add_edge(> 0> ,> 1> )> > graph.add_edge(> 0> ,> 4> )> > graph.add_edge(> 1> ,> 2> )> > graph.add_edge(> 1> ,> 3> )> > graph.add_edge(> 1> ,> 4> )> > graph.add_edge(> 2> ,> 3> )> > graph.add_edge(> 3> ,> 4> )> > graph.print_graph()>

Wyjście

Adjacency list of vertex 0 head ->4 -> 1 Lista sąsiedztwa wierzchołka 1 głowa -> 4 -> 3 -> 2 -> 0 Lista sąsiedztwa wierzchołka 2 głowa -> 3 -> 1 Lista sąsiedztwa wierzchołka 3 głowa -> 4 -> 2 -> 1 Sąsiedztwo lista wierzchołków 4 głowy -> 3 -> 1 -> 0 

Przechodzenie wykresu

Wyszukiwanie wszerz lub BFS

Przemierzanie wszerz dla wykresu jest podobny do przechodzenia drzewa w pierwszej kolejności. Jedynym haczykiem jest to, że w przeciwieństwie do drzew wykresy mogą zawierać cykle, więc możemy ponownie dojść do tego samego węzła. Aby uniknąć wielokrotnego przetwarzania węzła, używamy tablicy odwiedzanych wartości logicznych. Dla uproszczenia zakłada się, że wszystkie wierzchołki są osiągalne z wierzchołka początkowego.

Na przykład na poniższym grafie zaczynamy przechodzenie od wierzchołka 2. Kiedy dochodzimy do wierzchołka 0, szukamy wszystkich sąsiednich wierzchołków. 2 jest jednocześnie sąsiadującym wierzchołkiem 0. Jeśli nie zaznaczymy odwiedzonych wierzchołków, to 2 zostanie przetworzone ponownie i będzie to proces niekończący się. Przejście wszerz poniższego wykresu to 2, 0, 3, 1.

Python3

# Python3 Program to print BFS traversal> # from a given source vertex. BFS(int s)> # traverses vertices reachable from s.> from> collections> import> defaultdict> # This class represents a directed graph> # using adjacency list representation> class> Graph:> > # Constructor> > def> __init__(> self> ):> > # default dictionary to store graph> > self> .graph> => defaultdict(> list> )> > # function to add an edge to graph> > def> addEdge(> self> ,u,v):> > self> .graph[u].append(v)> > # Function to print a BFS of graph> > def> BFS(> self> , s):> > # Mark all the vertices as not visited> > visited> => [> False> ]> *> (> max> (> self> .graph)> +> 1> )> > # Create a queue for BFS> > queue> => []> > # Mark the source node as> > # visited and enqueue it> > queue.append(s)> > visited[s]> => True> > while> queue:> > # Dequeue a vertex from> > # queue and print it> > s> => queue.pop(> 0> )> > print> (s, end> => ' '> )> > # Get all adjacent vertices of the> > # dequeued vertex s. If a adjacent> > # has not been visited, then mark it> > # visited and enqueue it> > for> i> in> self> .graph[s]:> > if> visited[i]> => => False> :> > queue.append(i)> > visited[i]> => True> # Driver code> # Create a graph given in> # the above diagram> g> => Graph()> g.addEdge(> 0> ,> 1> )> g.addEdge(> 0> ,> 2> )> g.addEdge(> 1> ,> 2> )> g.addEdge(> 2> ,> 0> )> g.addEdge(> 2> ,> 3> )> g.addEdge(> 3> ,> 3> )> print> (> 'Following is Breadth First Traversal'> > ' (starting from vertex 2)'> )> g.BFS(> 2> )> # This code is contributed by Neelam Yadav>

Wyjście

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1 

Złożoność czasowa: O(V+E) gdzie V to liczba wierzchołków grafu, a E to liczba krawędzi grafu.

Głębokość pierwszego wyszukiwania lub DFS

Głębokość pierwszego przejścia dla wykresu jest podobne do pierwszego przejścia drzewa na głębokość. Jedynym haczykiem jest to, że w przeciwieństwie do drzew grafy mogą zawierać cykle, a węzeł można odwiedzić dwukrotnie. Aby uniknąć wielokrotnego przetwarzania węzła, użyj odwiedzanej tablicy logicznej.

Algorytm:

• Utwórz funkcję rekurencyjną, która pobiera indeks węzła i odwiedzaną tablicę.
• Oznacz bieżący węzeł jako odwiedzony i wydrukuj węzeł.
• Przejdź przez wszystkie sąsiednie i nieoznaczone węzły i wywołaj funkcję rekurencyjną z indeksem sąsiedniego węzła.

Python3

# Python3 program to print DFS traversal> # from a given graph> from> collections> import> defaultdict> # This class represents a directed graph using> # adjacency list representation> class> Graph:> > # Constructor> > def> __init__(> self> ):> > # default dictionary to store graph> > self> .graph> => defaultdict(> list> )> > # function to add an edge to graph> > def> addEdge(> self> , u, v):> > self> .graph[u].append(v)> > # A function used by DFS> > def> DFSUtil(> self> , v, visited):> > # Mark the current node as visited> > # and print it> > visited.add(v)> > print> (v, end> => ' '> )> > # Recur for all the vertices> > # adjacent to this vertex> > for> neighbour> in> self> .graph[v]:> > if> neighbour> not> in> visited:> > self> .DFSUtil(neighbour, visited)> > # The function to do DFS traversal. It uses> > # recursive DFSUtil()> > def> DFS(> self> , v):> > # Create a set to store visited vertices> > visited> => set> ()> > # Call the recursive helper function> > # to print DFS traversal> > self> .DFSUtil(v, visited)> # Driver code> # Create a graph given> # in the above diagram> g> => Graph()> g.addEdge(> 0> ,> 1> )> g.addEdge(> 0> ,> 2> )> g.addEdge(> 1> ,> 2> )> g.addEdge(> 2> ,> 0> )> g.addEdge(> 2> ,> 3> )> g.addEdge(> 3> ,> 3> )> print> (> 'Following is DFS from (starting from vertex 2)'> )> g.DFS(> 2> )>

Wyjście

Following is DFS from (starting from vertex 2) 2 0 1 3 

Złożoność czasowa: O(V + E), gdzie V to liczba wierzchołków, a E to liczba krawędzi grafu.