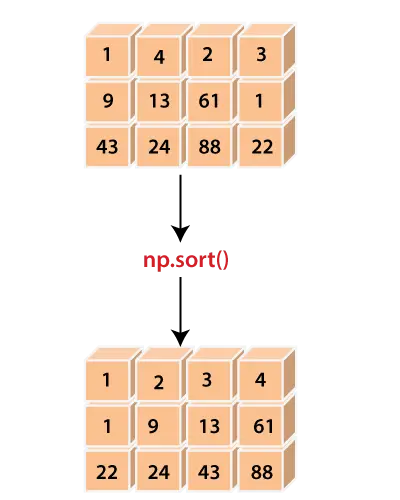
Maksymalna sterta w Javie

A maksymalna sterta to kompletne drzewo binarne, w którym wartość w każdym węźle wewnętrznym jest większa lub równa wartościom w elementach potomnych tego węzła. Mapowanie elementów sterty na tablicę jest proste: jeśli w węźle przechowywany jest indeks k, wówczas jego lewe dziecko jest przechowywane pod indeksem 2k + 1, a prawe dziecko pod indeksem 2k + 2.
Ilustracja: Maksymalna sterta

Jak jest reprezentowany Max Heap?
Heap A-Max jest kompletnym drzewem binarnym. Kopiec A-Max jest zwykle reprezentowany jako tablica. Element główny będzie znajdował się w Arr[0]. Poniższa tabela przedstawia indeksy innych węzłów dla it węzeł, tj. Arr[i]:
Arr[(i-1)/2] Zwraca węzeł nadrzędny.
Arr[(2*i)+1] Zwraca lewy węzeł podrzędny.
Arr[(2*i)+2] Zwraca prawy węzeł podrzędny.
Operacje na Max Heap są następujące:
- pobierzMax(): Zwraca element główny Max Heap. Złożoność czasowa tej operacji wynosi O(1) .
- ekstraktMaks.(): Usuwa maksymalny element z MaxHeap . Złożoność czasowa tej operacji wynosi O(Log n) ponieważ ta operacja wymaga zachowania właściwości sterty poprzez wywołanie metody metoda heapify(). po usunięciu korzenia.
- wstawić(): Włożenie nowego klucza trwa O(Log n) czas. Dodajemy nowy klucz na końcu drzewa. Jeśli nowy klucz jest mniejszy niż jego rodzic, nie musimy nic robić. W przeciwnym razie musimy przejść w górę, aby naprawić naruszoną właściwość sterty.
Notatka: W poniższej implementacji wykonujemy indeksowanie od indeksu 1, aby uprościć implementację.
Metody:
Istnieją 2 metody, dzięki którym możemy osiągnąć wymieniony cel:
- Podstawowe podejście poprzez tworzenie maxHeapify() metoda
- Za pomocą Kolekcje.reverseOrder() metoda poprzez bibliotekę Functions
Metoda 1: Podstawowe podejście poprzez tworzenie maxHeapify() metoda
Będziemy tworzyć metodę zakładając, że lewe i prawe poddrzewo są już skompletowane, pozostaje nam jedynie naprawić korzeń.
Przykład
Jawa
// Java program to implement Max Heap> // Main class> public> class> MaxHeap {> > private> int> [] Heap;> > private> int> size;> > private> int> maxsize;> > // Constructor to initialize an> > // empty max heap with given maximum> > // capacity> > public> MaxHeap(> int> maxsize)> > {> > // This keyword refers to current instance itself> > this> .maxsize = maxsize;> > this> .size => 0> ;> > Heap => new> int> [> this> .maxsize];> > }> > // Method 1> > // Returning position of parent> > private> int> parent(> int> pos) {> return> (pos -> 1> ) /> 2> ; }> > // Method 2> > // Returning left children> > private> int> leftChild(> int> pos) {> return> (> 2> * pos) +> 1> ; }> > // Method 3> > // Returning right children> > private> int> rightChild(> int> pos)> > {> > return> (> 2> * pos) +> 2> ;> > }> > // Method 4> > // Returning true if given node is leaf> > private> boolean> isLeaf(> int> pos)> > {> > if> (pos>(rozmiar /> 2> ) && pos <= size) {> > return> true> ;> > }> > return> false> ;> > }> > // Method 5> > // Swapping nodes> > private> void> swap(> int> fpos,> int> spos)> > {> > int> tmp;> > tmp = Heap[fpos];> > Heap[fpos] = Heap[spos];> > Heap[spos] = tmp;> > }> > // Method 6> > // Recursive function to max heapify given subtree> > private> void> maxHeapify(> int> pos)> > {> > if> (isLeaf(pos))> > return> ;> > if> (Heap[pos] || Heap[pos] if (Heap[leftChild(pos)]>Heap[rightChild(pos)]) { swap(pos, leftChild(pos)); maxHeapify(leftChild(pos)); } else { swap(pos, prawe dziecko(pos)); maxHeapify(rightChild(pos)); } } } // Metoda 7 // Wstawia nowy element do maksymalnej sterty public void wstaw(int element) { Heap[size] = element; // Przejdź w górę i napraw naruszoną właściwość int current = size; while (Sterta[bieżący]> Sterta[nadrzędny(bieżący)]) { swap(bieżący, nadrzędny(bieżący)); prąd = rodzic(bieżący); } rozmiar++; } // Metoda 8 // Aby wyświetlić stertę public void print() { for (int i = 0; i 2; i++) { System.out.print('Węzeł nadrzędny: ' + Heap[i]); if (leftChild(i) // jeśli dziecko znajduje się poza granicami // tablicy System.out.print(' Lewy węzeł podrzędny: ' + Heap[leftChild(i)]); if (rightChild(i ) // prawy indeks potomny nie może // znajdować się poza indeksem tablicy System.out.print(' Prawy węzeł potomny: ' + Heap[rightChild(i)]); System.out.println() ; // nowa linia } } // Metoda 9 // Usuń element z maksymalnej sterty public int ekstraktMax() { int popped = Heap[0] = Heap[--size]; ; return wyskoczył; } // Metoda 10 // Metoda głównego sterownika public static void main(String[] arg) { // Wyświetl komunikat dla lepszej czytelności System.out.println('Maksymalna sterta to '); = nowy MaxHeap(15); // Wstawianie węzłów // Niestandardowe wejścia maxHeap.insert(5); maxHeap.insert(17); maxHeap.insert(19); maxHeap.insert(22); maxHeap.insert(9); // Wywołanie maxHeap() zgodnie z definicją powyżej maxHeap.print(); wartość na stercie System.out.println('Maksymalna wartość to ' + maxHeap.extractMax()); } }> |
Wyjście
The Max Heap is Parent Node : 84 Left Child Node: 22 Right Child Node: 19 Parent Node : 22 Left Child Node: 17 Right Child Node: 10 Parent Node : 19 Left Child Node: 5 Right Child Node: 6 Parent Node : 17 Left Child Node: 3 Right Child Node: 9 The max val is 84
Metoda 2: Korzystanie z metody Collections.reverseOrder() za pośrednictwem funkcji bibliotecznych
Do implementacji Heaps w Javie używamy klasy PriorityQueue. Domyślnie ta klasa implementuje Min Heap. Aby zaimplementować Max Heap, używamy metody Collections.reverseOrder().
Przykład
Jawa
// Java program to demonstrate working> // of PriorityQueue as a Max Heap> // Using Collections.reverseOrder() method> // Importing all utility classes> import> java.util.*;> // Main class> class> GFG {> > // Main driver method> > public> static> void> main(String args[])> > {> > // Creating empty priority queue> > PriorityQueue pQueue> > => new> PriorityQueue(> > Collections.reverseOrder());> > // Adding items to our priority queue> > // using add() method> > pQueue.add(> 10> );> > pQueue.add(> 30> );> > pQueue.add(> 20> );> > pQueue.add(> 400> );> > // Printing the most priority element> > System.out.println(> 'Head value using peek function:'> > + pQueue.peek());> > // Printing all elements> > System.out.println(> 'The queue elements:'> );> > Iterator itr = pQueue.iterator();> > while> (itr.hasNext())> > System.out.println(itr.next());> > // Removing the top priority element (or head) and> > // printing the modified pQueue using poll()> > pQueue.poll();> > System.out.println(> 'After removing an element '> > +> 'with poll function:'> );> > Iterator itr2 = pQueue.iterator();> > while> (itr2.hasNext())> > System.out.println(itr2.next());> > // Removing 30 using remove() method> > pQueue.remove(> 30> );> > System.out.println(> 'after removing 30 with'> > +> ' remove function:'> );> > Iterator itr3 = pQueue.iterator();> > while> (itr3.hasNext())> > System.out.println(itr3.next());> > // Check if an element is present using contains()> > boolean> b = pQueue.contains(> 20> );> > System.out.println(> 'Priority queue contains 20 '> > +> 'or not?: '> + b);> > // Getting objects from the queue using toArray()> > // in an array and print the array> > Object[] arr = pQueue.toArray();> > System.out.println(> 'Value in array: '> );> > for> (> int> i => 0> ; i System.out.println('Value: ' + arr[i].toString()); } }> |
Wyjście
Head value using peek function:400 The queue elements: 400 30 20 10 After removing an element with poll function: 30 10 20 after removing 30 with remove function: 20 10 Priority queue contains 20 or not?: true Value in array: Value: 20 Value: 10