Programowanie liniowe
Programowanie liniowe jest pojęciem matematycznym używanym do znalezienia optymalnego rozwiązania funkcji liniowej. Metoda ta wykorzystuje proste założenia optymalizacji danej funkcji. Programowanie liniowe ma ogromne zastosowanie w świecie rzeczywistym i służy do rozwiązywania różnego rodzaju problemów.
Programowanie liniowe jest stosowane w różnych gałęziach przemysłu, takich jak przemysł żeglugowy, przemysł wytwórczy, przemysł transportowy, telekomunikacja i inne.
Termin programowanie liniowe składa się z dwóch słów liniowy i programowanie, słowo liniowe określa relację pomiędzy różnymi typami zmiennych pierwszego stopnia używanych w problemie, a słowo programowanie opisuje nam krok po kroku procedurę rozwiązywania tych problemów.
W tym artykule poznamy szczegółowo programowanie liniowe, jego przykłady, formuły i inne pojęcia.
Spis treści
- Co to jest programowanie liniowe?
- Elementy programowania liniowego
- Przykłady programowania liniowego
- Problemy programowania liniowego
- Rodzaje problemów programowania liniowego
- Formuła programowania liniowego
- Jak rozwiązać problemy z programowaniem liniowym?
- Metody programowania liniowego
- Metoda programowania liniowego Simplex
- Graficzna metoda programowania liniowego
- Zastosowania programowania liniowego
- Znaczenie programowania liniowego
- Aktualne zastosowania programowania liniowego
- Programowanie liniowe w badaniach operacyjnych
- Metoda Simplex
Co to jest programowanie liniowe?
Programowanie liniowe Lub Optymalizacja liniowa to technika, która pomaga nam znaleźć optymalne rozwiązanie danego problemu, optymalne rozwiązanie to rozwiązanie, które jest najlepszym możliwym wynikiem danego konkretnego problemu.
Krótko mówiąc, jest to metoda pozwalająca dowiedzieć się, jak zrobić coś w najlepszy możliwy sposób. Przy ograniczonych zasobach należy optymalnie wykorzystać zasoby i osiągnąć najlepszy możliwy wynik w określonym celu, takim jak najniższe koszty, najwyższa marża lub najkrótszy czas.
Sytuacją wymagającą poszukiwania najlepszych wartości zmiennych podlegających pewnym ograniczeniom jest sytuacja, w której wykorzystujemy problemy programowania liniowego. Sytuacji tych nie można rozwiązać za pomocą zwykłych technik obliczeniowych i numerycznych.
Definicja programowania liniowego
Programowanie liniowe to technika stosowana do optymalizacji konkretnego scenariusza. Stosowanie programowania liniowego zapewnia nam najlepszy możliwy wynik w danej sytuacji. Wykorzystuje wszystkie dostępne zasoby w taki sposób, aby przyniosły one optymalny rezultat.
Elementy programowania liniowego
Podstawowe elementy problemu programowania liniowego (LP) to:
- Zmienne decyzje: Zmienne, które chcesz określić, aby osiągnąć optymalne rozwiązanie.
- Funkcja celu: M równanie tematyczne, które reprezentuje cel, który chcesz osiągnąć
- Ograniczenia: Ograniczenia lub ograniczenia, których muszą przestrzegać zmienne decyzyjne.
- Ograniczenia nienegatywne: W niektórych w rzeczywistych scenariuszach zmienne decyzyjne nie mogą być ujemne
Dodatkowe cechy programowania liniowego
- Skończoność: Liczba zmiennych decyzyjnych i ograniczeń w problemie LP jest skończona.
- Liniowość: Funkcja celu i wszystkie ograniczenia muszą być funkcjami liniowymi zmiennych decyzyjnych . Oznacza to, że stopień zmiennych powinien wynosić jeden.
Przykłady programowania liniowego
Sytuacje, w których stosuje się programowanie liniowe, możemy zrozumieć na przykładzie omówionym poniżej,
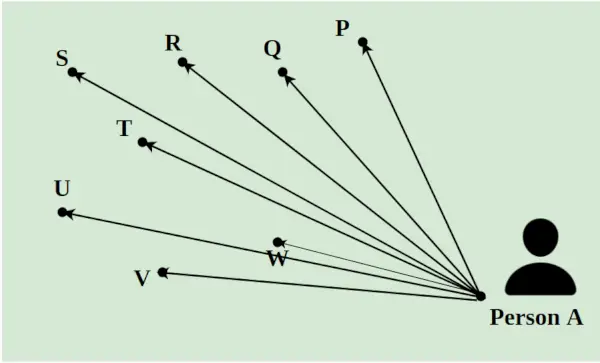
Załóżmy, że dostawca musi dostarczyć 8 paczek dziennie do różnych lokalizacji w mieście. Musi wybrać wszystkie pakiety z punktu A i dostarczyć je do punktów P, Q, R, S, T, U, V i W. Odległość między nimi jest oznaczona liniami jak na obrazku poniżej. Najkrótsza droga, którą podąża dostawca, jest obliczana przy użyciu koncepcji programowania liniowego.

Problemy programowania liniowego
Problemy z programowaniem liniowym (LPP) obejmują optymalizację funkcji liniowej w celu znalezienia optymalnego rozwiązania wartościowego dla tej funkcji. Wartość optymalna może być wartością maksymalną lub wartością minimalną.
W LPP wywoływane są funkcje liniowe funkcje obiektywne. Funkcja celu może mieć wiele zmiennych, które podlegają warunkom i muszą je spełniać ograniczenia liniowe .
Rodzaje problemów programowania liniowego
Istnieje wiele różnych problemów programowania liniowego (LPP), ale w tym artykule zajmiemy się trzema głównymi problemami programowania liniowego.
Problemy produkcyjne
Problemy produkcyjne to problem dotyczący liczby jednostek, które należy wyprodukować lub sprzedać, aby zmaksymalizować zyski, gdy każdy produkt wymaga stałej siły roboczej, godzin pracy maszyn i surowców.
Problemy z dietą
Służy do obliczania liczby różnych rodzajów składników, które należy uwzględnić w diecie, aby uzyskać minimalny koszt, w zależności od dostępności żywności i jej ceny.
Problemy transportowe
Służy do ustalenia harmonogramu transportu w celu znalezienia najtańszego sposobu transportu produktu z zakładów/fabryk znajdujących się w różnych lokalizacjach na różne rynki.
Formuła programowania liniowego
Problem programowania liniowego składa się z:
- Zmienne decyzje
- Funkcja celu
- Ograniczenia
- Ograniczenia nieujemne
Zmienne decyzje są zmiennymi x i y, które decydują o wynikach problemu programowania liniowego i reprezentują ostateczne rozwiązanie.
The funkcja celu , ogólnie reprezentowana przez Z, jest funkcją liniową, którą należy zoptymalizować zgodnie z danym warunkiem, aby uzyskać rozwiązanie końcowe.
The ograniczenia nałożone na zmienne decyzyjne, które ograniczają ich wartości, nazywane są ograniczeniami.
Ogólny wzór problemu programowania liniowego wygląda następująco:
Funkcja celu : Z = topór + by
Ograniczenia: cx + dy ≥ e, px + qy ≤ r
Ograniczenia nieujemne: x ≥ 0, y ≥ 0
W powyższym warunku x i y są zmiennymi decyzyjnymi.
Jak rozwiązać problemy z programowaniem liniowym?
Przed rozwiązaniem problemów programowania liniowego musimy najpierw sformułować problemy zgodnie ze standardowymi parametrami. Etapy rozwiązywania problemów z programowaniem liniowym to:
Krok 1: Zaznacz zmienne decyzyjne w zadaniu.
Krok 2: Zbuduj funkcję celu problemu i sprawdź, czy należy ją minimalizować, czy maksymalizować.
Krok 3: Zapisz wszystkie ograniczenia problemów liniowych.
Krok 4: Zapewnij nieujemne ograniczenia zmiennych decyzyjnych.
Krok 5: Teraz rozwiąż problem programowania liniowego dowolną metodą, zazwyczaj używamy metody simpleksowej lub graficznej.
Metody programowania liniowego
Stosujemy różne metody rozwiązywania problemów programowania liniowego. Dwie najczęściej stosowane metody to:
- Metoda Simplex
- Metoda graficzna
Przyjrzyjmy się szczegółowo tym dwóm metodom w tym artykule,
Metoda programowania liniowego Simplex
Jedną z najpopularniejszych metod rozwiązywania problemów programowania liniowego jest metoda sympleksowa. W tej metodzie powtarzamy określony warunek „n” kilka razy, aż do osiągnięcia optymalnego rozwiązania.
Kroki wymagane do rozwiązania problemów programowania liniowego przy użyciu metody simpleks to:
Krok 1: Formułować problemy programowania liniowego w oparciu o podane ograniczenia.
Krok 2: Przekształć wszystkie podane nierówności na równania lub równości problemów programowania liniowego, dodając zmienną luzu do każdej nierówności, jeśli jest to konieczne.
Krok 3: Skonstruuj początkową tabelę simplex. Reprezentując każde równanie ograniczenia w rzędzie i zapisując funkcję celu w dolnym wierszu. Otrzymana w ten sposób tabela nazywana jest tablicą Simplex.
Krok 4: Zidentyfikuj największy ujemny wpis w dolnym wierszu. Kolumna elementu z najwyższym ujemnym wpisem nazywana jest kolumną przestawną
Krok 5: Podziel wpisy w kolumnie znajdującej się najbardziej na prawo z wpisami w odpowiedniej kolumnie przestawnej, z wyłączeniem wpisów w wierszu położonym najniżej. Teraz wiersz zawierający najmniejszą liczbę wpisów nazywany jest wierszem przestawnym. Element obrotowy uzyskuje się poprzez przecięcie rzędu obrotowego i kolumny obrotowej.
Krok 6: Używając operacji macierzowej i za pomocą elementu obrotowego, spraw, aby wszystkie wpisy w kolumnie przestawnej miały wartość zerową.
Krok 7: Sprawdź, czy w najniższym wierszu nie ma wpisów ujemnych, jeśli w dolnym wierszu nie ma wpisów ujemnych, zakończ proces, w przeciwnym razie rozpocznij proces ponownie od kroku 4.
Krok 8: Otrzymana w ten sposób końcowa tabela simplex daje rozwiązanie naszego problemu.
Graficzna metoda programowania liniowego
Metoda graficzna jest inną metodą niż metoda Simplex, która służy do rozwiązywania problemów programowania liniowego. Jak sama nazwa wskazuje, metoda ta wykorzystuje wykresy do rozwiązywania zadanych problemów programowania liniowego. Jest to najlepsza metoda rozwiązywania problemów programowania liniowego i wymaga mniej wysiłku niż metoda simplex.
Metodą tą wykreślamy wszystkie nierówności, które podlegają ograniczeniom w zadanych zagadnieniach programowania liniowego. Gdy tylko wszystkie nierówności danego LPP zostaną naniesione na wykres XY, wspólny obszar wszystkich nierówności daje rozwiązanie optymalne. Obliczane są wszystkie punkty narożne obszaru wykonalnego i we wszystkich tych punktach obliczana jest wartość funkcji celu, a następnie porównując te wartości otrzymujemy optymalne rozwiązanie LPP.
Przykład: Znajdź maksymalną i minimalną wartość z = 6x + 9y, gdy warunki ograniczające są następujące:
- 2x + 3 lata ≤ 12
- x i y ≥ 0
- x + y ≤ 5
Rozwiązanie:
Krok 1 : Najpierw przekształć nierówności w równania normalne. Stąd równania będą miały postać 2x+3y = 0, x = 0, y = 0 i x + y = 5.
Krok 2 : Znajdź punkty, w których 2x + 3y i x + y = 5 przecinają osie x i y. Aby znaleźć punkt przecięcia osi x, wpisz y = 0 w odpowiednim równaniu i znajdź punkt. Podobnie dla punktów przecięcia osi Y wstaw x = 0 do odpowiedniego równania.
Krok 3 : Narysuj dwie linie przecinające oś X i Y. Stwierdzamy, że obie osie przecinają się w (3,2).
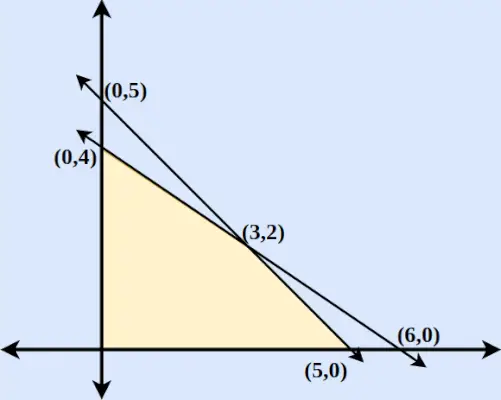
Krok 4 : Dla x ≥ 0 i y ≥ 0 stwierdzamy, że spełnione są obie nierówności. Zatem region będzie obejmował obszar ograniczony dwiema osiami i obiema liniami, łącznie z początkiem. Wykreślony obszar pokazano poniżej na rysunku.
Krok 5 : Znajdź Z dla każdego punktu oraz maksima i minima.
Współrzędne Z = 6x + 9 lat (0,5) Z = 45 (0,4) Z = 36 (5.0) Z = 30 (6,0) Z = 36 (3.2) Z = 36 Zatem stwierdzamy, że Z = 6x + 9y jest maksimum w (0,5) i minimum w (5,0).
Zastosowania programowania liniowego
Programowanie liniowe ma zastosowanie w różnych dziedzinach. Służy do znalezienia minimalnego kosztu procesu, gdy podane są wszystkie ograniczenia problemów. Służy do optymalizacji kosztów transportu pojazdu itp. Istnieją różne zastosowania programowania liniowego
Przemysły Inżynieryjne
Przemysł inżynieryjny wykorzystuje programowanie liniowe do rozwiązywania problemów projektowych i produkcyjnych oraz do uzyskania maksymalnej wydajności w danych warunkach.
Przemysły produkcyjne
Przemysł produkcyjny wykorzystuje programowanie liniowe w celu maksymalizacji zysków firm i zmniejszenia kosztów produkcji.
Przemysł Energetyczny
Przedsiębiorstwa energetyczne wykorzystują programowanie liniowe w celu optymalizacji swojej produkcji.
Przemysł transportowy
Programowanie liniowe jest również wykorzystywane w branży transportowej w celu znalezienia ścieżki minimalizującej koszty transportu.
Znaczenie programowania liniowego
Programowanie liniowe ma ogromne znaczenie w różnych gałęziach przemysłu, maksymalizuje wartość wyjściową, minimalizując wartości wejściowe zgodnie z różnymi ograniczeniami.
LP ma duże zastosowanie, gdy podczas rozwiązywania problemu mamy wiele warunków i musimy zoptymalizować wynik problemu, tj. musimy znaleźć minimalną lub maksymalną wartość zgodnie z danym warunkiem.
Czytaj więcej,
- Nierówności liniowe
- Algebraiczne rozwiązanie nierówności liniowych
Problemy programowania liniowego
Problem 1: Firma produkuje i sprzedaje dwa rodzaje produktów, a koszt wytworzenia każdej jednostki a i b wynosi odpowiednio 200 i 150 rupii, każda jednostka produktu przynosi zysk 20 rupii, a każda jednostka produktu b przynosi zysk 15 rupii na sprzedaży . Firma szacuje, że miesięczne zapotrzebowanie A i B będzie równe maksymalnej zebranej jednostce w całym budżecie produkcyjnym na dany miesiąc, ustalonym na 50000 rupii. Ile jednostek powinna wyprodukować firma, aby uzyskać maksymalny zysk z miesięcznej sprzedaży z oraz b?
Rozwiązanie:
Niech x = liczba jednostek typu A
y = liczba jednostek typu B
Maksymalizuj Z = 40x + 50y
Z zastrzeżeniem ograniczeń
3x + y ≤ 9
x + 2y ≤ 8
oraz x, y ≥ 0
Rozważ równanie,
3x + y = 9
x = 3
y = 0
i x + 2y = 8
x = 8
y = 0
Teraz możemy określić maksymalną wartość Z, oceniając wartość Z w czterech punktach (wierzchołkach), jak pokazano poniżej
Wierzchołki
Z = 40x + 50 lat
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Maksymalny zysk, Z = Rs. 230
∴ Liczba jednostek typu A wynosi 2, a liczba jednostek typu B wynosi 3.
Problem 2: Maksymalizuj Z = 3x + 4y.
Z zastrzeżeniem ograniczeń , x + y ≤ 450, 2x + y ≤ 600 i x, y ≤ 0.
Rozwiązanie:
Mamy z danego
Ograniczenia (1)
X + Y = 450
Umieszczenie x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Umieszczenie y = 0, ⇒ x + 0 = 450 ⇒ x = 450
Z, Ograniczenia (2)
2x + y = 600
Umieszczenie x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Umieszczenie y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Teraz mamy współrzędną punktów Z = 3x + 4y
| Wierzchołki | Z = 3x + 4y |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Zatem optymalne rozwiązanie ma maksimum Z = 1800 przy współrzędnych x = 0 i y = 450. Wykres przedstawiono poniżej.

Aktualne zastosowania programowania liniowego
Programowanie liniowe, potężna technika matematyczna, służy do rozwiązywania problemów optymalizacyjnych w różnych gałęziach przemysłu. Oto kilka nowoczesnych zastosowań:
- Optymalizacja łańcucha dostaw : Programowanie liniowe pomaga firmom minimalizować koszty i maksymalizować wydajność w łańcuchach dostaw. Służy do określania najbardziej opłacalnych tras transportu, operacji magazynowych i strategii zarządzania zapasami.
- Zarządzanie energią : W sektorze energetycznym stosuje się programowanie liniowe w celu optymalizacji zestawu metod produkcji energii. Obejmuje to równoważenie tradycyjnych źródeł energii z odnawialnymi źródłami energii w celu zmniejszenia kosztów i wpływu na środowisko przy jednoczesnym zaspokojeniu popytu.
- Projektowanie sieci telekomunikacyjnej : Programowanie liniowe pomaga w projektowaniu wydajnych sieci telekomunikacyjnych. Pomaga w alokacji przepustowości, projektowaniu układów sieci i optymalizacji przepływu danych, aby zapewnić szybką komunikację przy niższych kosztach.
- Planowanie finansowe : Firmy i analitycy finansowi korzystają z programowania liniowego w celu optymalizacji portfela, zarządzania ryzykiem i budżetowania kapitałowego. Pomaga w podejmowaniu decyzji inwestycyjnych maksymalizujących zyski przy jednoczesnej minimalizacji ryzyka.
- Logistyka w służbie zdrowia : W opiece zdrowotnej stosuje się programowanie liniowe w celu optymalizacji alokacji zasobów, takich jak łóżka szpitalne, personel medyczny i sprzęt. Ma to kluczowe znaczenie dla poprawy opieki nad pacjentem, skrócenia czasu oczekiwania i efektywnego zarządzania kosztami.
- Optymalizacja procesu produkcyjnego : Programowanie liniowe służy do określenia optymalnych poziomów produkcji wielu produktów w zakładzie produkcyjnym, biorąc pod uwagę ograniczenia, takie jak siła robocza, materiały i dostępność maszyn.
- Planowanie rolnictwa : Rolnicy i planiści rolni korzystają z programowania liniowego, aby decydować o wyborze upraw, użytkowaniu gruntów i alokacji zasobów w celu maksymalizacji plonów i zysków przy jednoczesnej ochronie zasobów.
- Harmonogram pracy załogi linii lotniczych : Linie lotnicze stosują programowanie liniowe w celu efektywnego planowania załóg, zapewniając, że personel podczas lotów będzie zgodny z przepisami i minimalizując koszty operacyjne.
Aplikacje te demonstrują wszechstronność i siłę programowania liniowego w rozwiązywaniu złożonych problemów optymalizacyjnych w różnych sektorach, ukazując jego znaczenie w dzisiejszym świecie opartym na danych.
Programowanie liniowe w badaniach operacyjnych
- Podstawowe narzędzie : Programowanie liniowe jest podstawowym narzędziem w badaniach operacyjnych służącym optymalizacji zasobów.
- Podejmowanie decyzji : Pomaga w podejmowaniu najlepszych decyzji dotyczących alokacji zasobów, maksymalizacji zysków lub minimalizacji kosztów.
- Szerokie zastosowania : Stosowany w różnych dziedzinach, takich jak logistyka, produkcja, finanse i opieka zdrowotna, do rozwiązywania złożonych problemów.
- Modelowanie problemów świata rzeczywistego : Przekształca problemy świata rzeczywistego w modele matematyczne w celu znalezienia najbardziej efektywnych rozwiązań.
Metoda Simplex
- Algorytm optymalizacji : Metoda Simplex to potężny algorytm stosowany w programowaniu liniowym w celu znalezienia optymalnego rozwiązania nierówności liniowych.
- Podejście krok po kroku : Iteracyjnie zmierza w stronę najlepszego rozwiązania, poruszając się po krawędziach obszaru wykonalnego określonego przez ograniczenia.
- Efektywność : Znany ze swojej skuteczności w rozwiązywaniu problemów programowania liniowego na dużą skalę.
- Wszechstronność : Ma zastosowanie w różnych dziedzinach, takich jak planowanie diety, przepływy sieciowe, planowanie produkcji i nie tylko, co świadczy o jego wszechstronności.
Programowanie liniowe – często zadawane pytania
Co to jest programowanie liniowe?
Programowanie liniowe to koncepcja matematyczna używana do optymalizacji danego problemu liniowego, który ma wiele ograniczeń. Stosując programowanie liniowe uzyskujemy optymalne rozwiązanie danego problemu
Jakie są problemy z programowaniem liniowym?
Problemy programowania liniowego (LPP) to problemy, które dają optymalne rozwiązanie danych warunków.
Co to jest wzór programowania liniowego?
Ogólne formuły programowania liniowego to:
- Funkcja celu: Z = topór + by
- Ograniczenia: px + qy ≤ r, sx + ty ≤ u
- Ograniczenia nieujemne: x ≥ 0, y ≥ 0
Jakie są różne typy programowania liniowego?
Różne typy metod programowania liniowego to:
- Programowanie liniowe metodą Simplex
- Programowanie liniowe metodą R
- Programowanie liniowe metodą graficzną
Jakie są wymagania programowania liniowego?
Różne wymagania problemów programowania liniowego to:
- Liniowość
- Funkcja celu
- Ograniczenia
- Nienegatywność
Jakie są zalety programowania liniowego?
Różne zalety programowania liniowego to:
- Zapewnia optymalne rozwiązanie dowolnego problemu liniowego.
- Jest łatwy w użyciu i zawsze daje spójne wyniki
- Pomaga maksymalizować zyski i zmniejszać koszty wejściowe.