Ten samouczek jest przewodnikiem przyjaznym dla początkujących uczenie się struktur danych i algorytmów za pomocą Pythona. W tym artykule omówimy wbudowane struktury danych, takie jak listy, krotki, słowniki itp., a także niektóre struktury danych zdefiniowane przez użytkownika, takie jak połączone listy , drzewa , wykresy itp. oraz algorytmy przechodzenia, wyszukiwania i sortowania za pomocą dobrych i dobrze wyjaśnionych przykładów oraz pytań ćwiczeniowych.

Listy

Listy Pythona są uporządkowanymi zbiorami danych, podobnie jak tablice w innych językach programowania. Pozwala na różne typy elementów na liście. Implementacja Python List jest podobna do Vectors w C++ lub ArrayList w JAVA. Kosztowną operacją jest wstawienie lub usunięcie elementu z początku Listy, gdyż konieczne jest przesunięcie wszystkich elementów. Wstawianie i usuwanie na końcu listy może być również kosztowne w przypadku zapełnienia wcześniej przydzielonej pamięci.

Przykład: tworzenie listy Pythona

List = [1, 2, 3, 'GFG', 2.3] print(List) 

[1, 2, 3, 'GFG', 2.3] 

Dostęp do elementów listy można uzyskać poprzez przypisany indeks. W indeksie początkowym listy w Pythonie sekwencja wynosi 0, a indeks końcowy to (jeśli jest tam N elementów) N-1.

Przykład: operacje na listach w Pythonie

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3]) 

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks 

Krotka

Krotki Pythona są podobne do list, ale krotki są niezmienny ma charakter naturalny, tj. raz stworzony nie może być modyfikowany. Podobnie jak lista, krotka może również zawierać elementy różnych typów.

W Pythonie krotki tworzy się poprzez umieszczenie sekwencji wartości oddzielonych „przecinkiem” z użyciem nawiasów lub bez nich w celu grupowania sekwencji danych.

Notatka: Aby utworzyć krotkę jednego elementu, musi znajdować się na końcu przecinek. Na przykład (8,) utworzy krotkę zawierającą 8 jako element.

Przykład: operacje na krotkach w Pythonie

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3]) 

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 

Ustawić

Zestaw Pythona to zmienny zbiór danych, który nie pozwala na powielanie. Zestawy są zasadniczo używane do testowania członkostwa i eliminowania duplikatów wpisów. Wykorzystana w tym struktura danych to Hashing, popularna technika wykonywania wstawiania, usuwania i przeglądania średnio w O(1).

Jeśli w tej samej pozycji indeksu znajduje się wiele wartości, wówczas wartość jest dodawana do tej pozycji indeksu, tworząc listę połączoną. W tym zestawie zestawy CPython są implementowane przy użyciu słownika ze zmiennymi fikcyjnymi, w których kluczowe elementy są ustawiane przez członków z większymi optymalizacjami pod kątem złożoności czasowej.

Implementacja zestawu:

Zestawy z wieloma operacjami na pojedynczej tabeli HashTable:

Przykład: operacje na zestawach w Pythonie

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set) 

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True 

Zamrożone zestawy

Zestawy mrożone w Pythonie są niezmienne obiekty, które obsługują tylko metody i operatory, które dają wynik bez wpływu na zamrożony zestaw lub zestawy, do których są stosowane. Chociaż elementy zestawu można modyfikować w dowolnym momencie, elementy zamrożonego zestawu pozostają takie same po utworzeniu.

Przykład: zestaw Python Frozen

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h') 

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'}) 

Strunowy

Ciągi Pythona to niezmienna tablica bajtów reprezentujących znaki Unicode. Python nie ma znakowego typu danych, pojedynczy znak to po prostu ciąg znaków o długości 1.

Notatka: Ponieważ ciągi znaków są niezmienne, modyfikacja ciągu spowoduje utworzenie nowej kopii.

Przykład: operacje na ciągach znaków w języku Python

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1]) 

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s 

Słownik

Słownik Pythona to nieuporządkowany zbiór danych, który przechowuje dane w formacie pary klucz:wartość. To jest jak tablice mieszające w jakimkolwiek innym języku ze złożonością czasową O(1). Indeksowanie słownika Pythona odbywa się za pomocą kluczy. Są to dowolne typy haszujące, tj. obiekty, których nigdy nie można zmieniać, jak ciągi znaków, liczby, krotki itp. Słownik możemy utworzyć za pomocą nawiasów klamrowych ({}) lub rozumienia słownikowego.

Przykład: operacje słownikowe w Pythonie

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict) 

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} 

Matryca

Macierz to tablica 2D, w której każdy element ma dokładnie ten sam rozmiar. Aby utworzyć macierz, będziemy używać Pakiet NumPy .

Przykład: operacje na macierzach NumPy w Pythonie

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m) 

Wyjście

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] 

Bajtearray

Python Bytearray daje zmienną sekwencję liczb całkowitych z zakresu 0 <= x < 256.

Przykład: operacje na bajtarray w Pythonie

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a) 

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e') 

Połączona lista

A połączona lista to liniowa struktura danych, w której elementy nie są przechowywane w sąsiadujących lokalizacjach pamięci. Elementy na połączonej liście są połączone za pomocą wskaźników, jak pokazano na poniższym obrazku:

Połączona lista jest reprezentowana przez wskaźnik do pierwszego węzła połączonej listy. Pierwszy węzeł nazywany jest głową. Jeśli połączona lista jest pusta, wartość nagłówka wynosi NULL. Każdy węzeł na liście składa się z co najmniej dwóch części:

• Dane
• Wskaźnik (lub odniesienie) do następnego węzła

Przykład: definiowanie listy połączonej w Pythonie

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None 

Stwórzmy prostą listę połączoną z 3 węzłami.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | zero | | 3 | zero |  +--------+------+ +--------+------+ +--------+------+ ''' sekunda.następna = trzecia ; # Połącz drugi węzeł z trzecim węzłem ''' Teraz następny z drugiego Węzeł odnosi się do trzeciego. Zatem wszystkie trzy węzły są połączone.  llist.head drugi trzeci | | |  | | |  +--------+------+ +--------+------+ +--------+------+ | 1 | o-------->| 2 | o-------->| 3 | zero |  +--------+------+ +--------+------+ +--------+------+ ''' 

Przeglądanie połączonej listy

W poprzednim programie utworzyliśmy prostą listę połączoną z trzema węzłami. Przejdźmy przez utworzoną listę i wydrukujmy dane każdego węzła. Na potrzeby przechodzenia napiszmy uniwersalną funkcję printList(), która wypisuje dowolną listę.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList() 

1 2 3 

Więcej artykułów na liście połączonej

• Wstawianie listy połączonej
• Usuwanie listy połączonej (Usunięcie danego klucza)
• Usuwanie listy połączonej (Usunięcie klucza na danej pozycji)
• Znajdź długość połączonej listy (iteratywne i rekurencyjne)
• Wyszukiwanie elementu na liście połączonej (iteracyjne i rekurencyjne)
• N-ty węzeł od końca listy połączonej
• Odwróć połączoną listę

A stos to liniowa struktura danych, która przechowuje elementy w sposób „ostatnie weszło/pierwsze wyszło” (LIFO) lub „pierwsze weszło/ostatni wyszło” (FILO). W stosie nowy element jest dodawany na jednym końcu, a element jest usuwany tylko z tego końca. Operacje wstawiania i usuwania są często nazywane push i pop.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty 

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: [] 

Jako stos, kolejka to liniowa struktura danych, w której przechowywane są pozycje według zasady „pierwsze weszło, pierwsze wyszło” (FIFO). W przypadku kolejki ostatnio dodany element jest usuwany jako pierwszy. Dobrym przykładem kolejki jest dowolna kolejka konsumentów do zasobu, w której konsument, który przyszedł pierwszy, jest obsługiwany jako pierwszy.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty 

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements [] 

Kolejki priorytetowe to abstrakcyjne struktury danych, w których każde dane/wartość w kolejce mają określony priorytet. Na przykład w liniach lotniczych bagaż z tytułem Biznes lub Pierwsza klasa przybywa wcześniej niż reszta. Kolejka priorytetowa jest rozszerzeniem kolejki o następujących właściwościach.

• Element o wysokim priorytecie jest usuwany z kolejki przed elementem o niskim priorytecie.
• Jeżeli dwa elementy mają ten sam priorytet, są obsługiwane zgodnie z kolejnością w kolejce.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] zwraca element z wyjątkiem IndexError: print() exit() if __name__ == '__main__': mojaQueue = PriorityQueue( ) mojaKolejka.insert(12) mojaKolejka.insert(1) mojaKolejka.insert(14) mojaKolejka.insert(7) print(mojaKolejka) dopóki nie jest myQueue.isEmpty(): print(myQueue.delete()) 

12 1 14 7 14 12 7 1 

Sterta

moduł sterty w Pythonie zapewnia strukturę danych sterty, która jest używana głównie do reprezentowania kolejki priorytetowej. Właściwość tej struktury danych polega na tym, że zawsze daje najmniejszy element (min. stertę) za każdym razem, gdy element jest otwierany. Za każdym razem, gdy elementy są wypychane lub otwierane, struktura sterty zostaje zachowana. Element sterty[0] również zwraca za każdym razem najmniejszy element. Obsługuje ekstrakcję i wstawianie najmniejszego elementu w czasach O (log n).

Ogólnie rzecz biorąc, sterty mogą być dwojakiego rodzaju:

• Maksymalna sterta: W Max-Heap klucz obecny w węźle głównym musi być największy spośród kluczy obecnych we wszystkich jego dzieciach. Ta sama właściwość musi być rekurencyjnie prawdziwa dla wszystkich poddrzew w tym drzewie binarnym.
• Minimalna sterta: W Min-Heap klucz obecny w węźle głównym musi być co najmniej kluczem spośród kluczy obecnych u wszystkich jego dzieci. Ta sama właściwość musi być rekurencyjnie prawdziwa dla wszystkich poddrzew w tym drzewie binarnym.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li)) 

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1 

Więcej artykułów na temat Heap

• Kopia binarna
• K’-ty największy element w tablicy
• K’th najmniejszy/największy element w nieposortowanej tablicy
• Sortuj prawie posortowaną tablicę
• Ciągła podtablica K-tej największej sumy
• Minimalna suma dwóch liczb utworzonych z cyfr tablicy

Drzewo to hierarchiczna struktura danych, która wygląda jak na poniższym rysunku –

 tree  ----  j  <-- root  /   f k  /   a h z  <-- leaves 

Najwyższy węzeł drzewa nazywany jest korzeniem, natomiast węzły położone najniżej lub węzły nieposiadające dzieci nazywane są węzłami liściowymi. Węzły znajdujące się bezpośrednio pod węzłem nazywane są jego dziećmi, a węzły znajdujące się bezpośrednio nad czymś nazywane są jego rodzicami.

A drzewo binarne to drzewo, którego elementy mogą mieć prawie dwoje dzieci. Ponieważ każdy element drzewa binarnego może mieć tylko 2 dzieci, zazwyczaj nazywamy je lewym i prawym dzieckiem. Węzeł drzewa binarnego zawiera następujące części.

• Dane
• Wskaźnik do lewego dziecka
• Wskaźnik do odpowiedniego dziecka

Przykład: definiowanie klasy węzła

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key 

Stwórzmy teraz drzewo z 4 węzłami w Pythonie. Załóżmy, że struktura drzewa wygląda jak poniżej –

 tree  ----  1  <-- root  /   2 3   /  4 

Przykład: Dodawanie danych do drzewa

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None''' 

Przejście przez drzewo

Drzewa można przemierzać na różne sposoby. Poniżej przedstawiono ogólnie stosowane sposoby przechodzenia przez drzewa. Rozważmy poniższe drzewo –

 tree  ----  1  <-- root  /   2 3   /  4 5 

Pierwsze przejścia na głębokość:

• Inorder (lewy, główny, prawy): 4 2 5 1 3
• Zamawianie w przedsprzedaży (główny, lewy, prawy): 1 2 4 5 3
• Postorder (lewy, prawy, główny): 4 5 2 3 1

Algorytm Inorder(drzewo)

• Przejdź przez lewe poddrzewo, tj. wywołaj Inorder(lewe poddrzewo)
• Odwiedź korzeń.
• Przejdź przez prawe poddrzewo, tj. wywołaj Inorder(prawe poddrzewo)

Algorytm w przedsprzedaży (drzewo)

• Odwiedź korzeń.
• Przejdź przez lewe poddrzewo, tj. wywołaj Preorder(lewe poddrzewo)
• Przejdź przez prawe poddrzewo, tj. wywołaj Preorder(prawe poddrzewo)

Algorytm Przekaz pocztowy (drzewo)

• Przejdź przez lewe poddrzewo, tj. wywołaj Postorder(lewe poddrzewo)
• Przejdź przez prawe poddrzewo, tj. wywołaj Postorder(prawe poddrzewo)
• Odwiedź korzeń.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root) 

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1 

Złożoność czasowa – O(n)

Przechodzenie według szerokości lub kolejności poziomów

Przechodzenie przez poziom drzewa oznacza przejście drzewa wszerz. Kolejność poziomów w powyższym drzewie wynosi 1 2 3 4 5.

Dla każdego węzła najpierw odwiedzany jest węzeł, a następnie jego węzły podrzędne umieszczane są w kolejce FIFO. Poniżej znajduje się algorytm dla tego samego -

• Utwórz pustą kolejkę q
• temp_node = root /*zacznij od katalogu głównego*/
• Zapętlaj, gdy temp_node nie ma wartości NULL
  • wydrukuj węzeł temp_>dane.
  • Umieść w kolejce dzieci temp_node (najpierw lewe, potem prawe) do q
  • Usuń z kolejki węzeł z q

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Wydrukuj początek kolejki i # usuń go z kolejki print (queue[0].data) węzeł = kolejka.pop(0) # Umieść w kolejce lewe dziecko, jeśli node.left nie jest Brak: kolejka.append(node.left ) # Umieść w kolejce prawe dziecko, jeśli node.right nie jest None: kolejka.append(node.right) # Program sterownika do testowania powyższej funkcji root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Węzeł(4) root.left.right = Węzeł(5) print ('Przechodzenie kolejności poziomów w drzewie binarnym to -') printLevelOrder(root) 

Level Order Traversal of binary tree is - 1 2 3 4 5 

Złożoność czasowa: O(n)

Więcej artykułów na temat drzewa binarnego

• Wstawienie do drzewa binarnego
• Usuwanie w drzewie binarnym
• Przechodzenie przez drzewo Inorder bez rekurencji
• Inorder Tree Traversal bez rekurencji i bez stosu!
• Drukuj przejścia postorderowe z podanych przejść Inorder i Preorder
• Znajdź przejście BST po zamówieniu z przejścia w przedsprzedaży

Drzewo wyszukiwania binarnego to binarna struktura danych oparta na węzłach, która ma następujące właściwości:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val  < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key) 

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val  < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r) 

20 30 40 50 60 70 80 

A wykres jest nieliniową strukturą danych składającą się z węzłów i krawędzi. Węzły są czasami nazywane także wierzchołkami, a krawędzie to linie lub łuki łączące dowolne dwa węzły na wykresie. Bardziej formalnie graf można zdefiniować jako graf składający się ze skończonego zestawu wierzchołków (lub węzłów) i zestawu krawędzi łączących parę węzłów.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0 <=vtx <=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix()) 

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Program sterownika dla powyższej klasy wykresu if __name__ == '__main__' : V = 5 graph = Wykres(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph() 

Adjacency list of vertex 0 head ->4 -> 1 Lista sąsiedztwa wierzchołka 1 głowa -> 4 -> 3 -> 2 -> 0 Lista sąsiedztwa wierzchołka 2 głowa -> 3 -> 1 Lista sąsiedztwa wierzchołka 3 głowa -> 4 -> 2 -> 1 Sąsiedztwo lista wierzchołków 4 głowy -> 3 -> 1 -> 0 

Przemierzanie wszerz dla wykresu jest podobny do przechodzenia drzewa w pierwszej kolejności. Jedynym haczykiem jest to, że w przeciwieństwie do drzew wykresy mogą zawierać cykle, więc możemy ponownie dojść do tego samego węzła. Aby uniknąć wielokrotnego przetwarzania węzła, używamy tablicy odwiedzanych wartości logicznych. Dla uproszczenia zakłada się, że wszystkie wierzchołki są osiągalne z wierzchołka początkowego.

Na przykład na poniższym grafie zaczynamy przechodzenie od wierzchołka 2. Kiedy dochodzimy do wierzchołka 0, szukamy wszystkich sąsiednich wierzchołków. 2 jest jednocześnie sąsiadującym wierzchołkiem 0. Jeśli nie zaznaczymy odwiedzonych wierzchołków, to 2 zostanie przetworzone ponownie i będzie to proces niekończący się. Przejście wszerz poniższego wykresu to 2, 0, 3, 1.

# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2) 

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1 

Złożoność czasowa: O(V+E) gdzie V to liczba wierzchołków grafu, a E to liczba krawędzi grafu.

Głębokość pierwszego wyszukiwania lub DFS

Głębokość pierwszego przejścia dla wykresu jest podobne do pierwszego przejścia drzewa na głębokość. Jedynym haczykiem jest to, że w przeciwieństwie do drzew grafy mogą zawierać cykle, a węzeł można odwiedzić dwukrotnie. Aby uniknąć wielokrotnego przetwarzania węzła, użyj odwiedzanej tablicy logicznej.

Algorytm:

• Utwórz funkcję rekurencyjną, która pobiera indeks węzła i odwiedzaną tablicę.
• Oznacz bieżący węzeł jako odwiedzony i wydrukuj węzeł.
• Przejdź przez wszystkie sąsiednie i nieoznaczone węzły i wywołaj funkcję rekurencyjną z indeksem sąsiedniego węzła.

# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2) 

Following is DFS from (starting from vertex 2) 2 0 1 3 

Więcej artykułów na wykresie

• Reprezentacje wykresów przy użyciu zestawu i skrótu
• Znajdź wierzchołek macierzysty na grafie
• Iteracyjne pierwsze przeszukiwanie głębokości
• Policz liczbę węzłów na danym poziomie w drzewie za pomocą BFS
• Policz wszystkie możliwe ścieżki między dwoma wierzchołkami

Proces, w którym funkcja wywołuje samą siebie bezpośrednio lub pośrednio, nazywa się rekurencją, a odpowiadająca jej funkcja nazywa się a funkcja rekurencyjna . Stosując algorytmy rekurencyjne, niektóre problemy można rozwiązać dość łatwo. Przykładami takich problemów są Wieże Hanoi (TOH), przechodzenie przez drzewo w zamówieniu/przedsprzedaży/po zamówieniu, DFS of Graph itp.

def fact(n):  # base case  if (n  <= 1)   return 1  else   return n*fact(n-1) 

# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test  < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test) 

3 2 1 1 2 3 

• Rekurencja
• Rekurencja w Pythonie
• Ćwicz pytania dotyczące rekurencji | Zestaw 1
• Ćwicz pytania dotyczące rekurencji | Zestaw 2
• Ćwicz pytania dotyczące rekurencji | Zestaw 3
• Ćwicz pytania dotyczące rekurencji | Zestaw 4
• Ćwicz pytania dotyczące rekurencji | Zestaw 5
• Ćwicz pytania dotyczące rekurencji | Zestaw 6
• Ćwicz pytania dotyczące rekurencji | Zestaw 7

>>> Więcej

Programowanie dynamiczne

Programowanie dynamiczne jest głównie optymalizacją w stosunku do zwykłej rekurencji. Gdziekolwiek widzimy rozwiązanie rekurencyjne, które powtarza wywołania tych samych danych wejściowych, możemy je zoptymalizować za pomocą programowania dynamicznego. Pomysł polega na tym, aby po prostu przechowywać wyniki podproblemów, abyśmy nie musieli później ich ponownie obliczać, gdy zajdzie taka potrzeba. Ta prosta optymalizacja redukuje złożoność czasową z wykładniczej do wielomianowej. Na przykład, jeśli napiszemy proste rekurencyjne rozwiązanie liczb Fibonacciego, otrzymamy wykładniczą złożoność czasową, a jeśli zoptymalizujemy ją poprzez przechowywanie rozwiązań podproblemów, złożoność czasowa sprowadzi się do liniowej.

Tabulacja a zapamiętywanie

Istnieją dwa różne sposoby przechowywania wartości, aby można było ponownie wykorzystać wartości podproblemu. Tutaj omówione zostaną dwa wzorce rozwiązywania problemu programowania dynamicznego (DP):

• Tabulacja: Od dołu do góry
• Zapamiętywanie: Z góry na dół

Tabulacja

Jak sama nazwa wskazuje zaczynając od dołu i kumulując odpowiedzi aż do góry. Porozmawiajmy o zmianie stanu.

Opiszmy stan naszego problemu DP jako dp[x] z dp[0] jako stanem podstawowym i dp[n] jako stanem docelowym. Musimy więc znaleźć wartość stanu docelowego, tj. dp[n].

Jeśli rozpoczniemy przejście od naszego stanu bazowego, tj. dp[0] i podążamy za naszą relacją przejścia stanu, aby osiągnąć nasz stan docelowy dp[n], nazywamy to podejściem oddolnym, ponieważ jest całkiem jasne, że rozpoczęliśmy nasze przejście od stanu docelowego dolny stan podstawowy i osiągnął najwyższy pożądany stan.

Dlaczego nazywamy to metodą tabulacji?

Aby to wiedzieć, napiszmy najpierw kod obliczający silnię liczby przy użyciu podejścia oddolnego. Po raz kolejny w ramach naszej ogólnej procedury rozwiązywania DP najpierw definiujemy stan. W tym przypadku definiujemy stan jako dp[x], gdzie dp[x] oznacza silnię x.

Teraz jest całkiem oczywiste, że dp[x+1] = dp[x] * (x+1)

# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i 

Zapamiętywanie

Jeszcze raz opiszmy to w kategoriach przejścia stanu. Jeśli potrzebujemy znaleźć wartość jakiegoś stanu, powiedzmy dp[n] i zamiast zaczynać od stanu bazowego, czyli dp[0], prosimy o odpowiedź od stanów, które mogą osiągnąć stan docelowy dp[n] po przejściu stanu relacji, to jest to odgórna moda DP.

Tutaj rozpoczynamy naszą podróż od najwyższego stanu docelowego i obliczamy jego odpowiedź, biorąc pod uwagę wartości stanów, które mogą osiągnąć stan docelowy, aż do osiągnięcia najniższego stanu bazowego.

Jeszcze raz napiszmy kod problemu silniowego w sposób odgórny

# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1)) 

Więcej artykułów na temat programowania dynamicznego

• Optymalna właściwość podbudowy
• Właściwość nakładających się podproblemów
• Liczby Fibonacciego
• Podzbiór z sumą podzielną przez m
• Podciąg rosnący maksymalnej sumy
• Najdłuższy wspólny podciąg

>>> Więcej

Algorytmy wyszukiwania

Wyszukiwanie liniowe

• Zacznij od lewego elementu arr[] i jeden po drugim porównaj x z każdym elementem arr[]
• Jeśli x pasuje do elementu, zwróć indeks.
• Jeśli x nie pasuje do żadnego z elementów, zwróć -1.

# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result) 

Element is present at index 3 

Złożoność czasowa powyższego algorytmu wynosi O(n).

Aby uzyskać więcej informacji, zobacz Wyszukiwanie liniowe .

Wyszukiwanie binarne

Przeszukuj posortowaną tablicę, wielokrotnie dzieląc interwał wyszukiwania na pół. Rozpocznij od interwału obejmującego całą tablicę. Jeśli wartość klucza wyszukiwania jest mniejsza niż pozycja w środku przedziału, zawęź przedział do dolnej połowy. W przeciwnym razie zawęź go do górnej połowy. Sprawdzaj wielokrotnie, aż zostanie znaleziona wartość lub przedział będzie pusty.

# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Jeśli element jest obecny w samym środku if arr[mid] == x: return mid # Jeśli element jest mniejszy niż środek, to # może być obecny tylko w lewej podtablicy elif arr[mid]> x: return binarySearch(arr, l, mid-1, x) # W innym przypadku element może występować tylko # w prawej podtablicy else: return binarySearch(arr, mid + 1, r, x ) else: # Element nie występuje w tablicy return -1 # Kod sterownika arr = [ 2, 3, 4, 10, 40 ] x = 10 # Wynik wywołania funkcji = binarySearch(arr, 0, len(arr)-1 , x) if wynik != -1: print ('Element występuje w indeksie % d' % wyniku) else: print ('Element nie występuje w tablicy') 

Element is present at index 3 

Złożoność czasowa powyższego algorytmu wynosi O(log(n)).

Aby uzyskać więcej informacji, zobacz Wyszukiwanie binarne .

Algorytmy sortowania

Sortowanie przez wybór

The sortowanie przez wybór algorytm sortuje tablicę, wielokrotnie znajdując minimalny element (biorąc pod uwagę kolejność rosnącą) z nieposortowanej części i umieszczając go na początku. W każdej iteracji sortowania przez wybór wybierany jest minimalny element (biorąc pod uwagę porządek rosnący) z nieposortowanej podtablicy i przenoszony do posortowanej podtablicy.

Schemat blokowy sortowania przez wybór:

# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Zamień znaleziony element minimalny na # pierwszy element A[i], A[min_idx] = A[min_idx], A[i] # Kod sterownika do przetestowania powyżej wydruku ('Tablica posortowana ') dla i w zakresie(dł(A)): print('%d' %A[i]), 

Sorted array 11 12 22 25 64 

Złożoność czasowa: NA ² ), ponieważ istnieją dwie zagnieżdżone pętle.

Przestrzeń pomocnicza: O(1)

Sortowanie bąbelkowe

Sortowanie bąbelkowe to najprostszy algorytm sortowania, który polega na wielokrotnym zamienianiu sąsiednich elementów, jeśli są w niewłaściwej kolejności.

Ilustracja:

# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Kod sterownika do przetestowania powyżej arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Posortowana tablica to:') dla i w zakresie(len(arr)): print ('%d' %arr[i]), 

Sorted array is: 11 12 22 25 34 64 90 

Złożoność czasowa: NA ² )

Sortowanie przez wstawianie

Aby posortować tablicę o rozmiarze n w kolejności rosnącej, użyj sortowanie przez wstawianie :

• Wykonaj iterację od arr[1] do arr[n] po tablicy.
• Porównaj bieżący element (klucz) z jego poprzednikiem.
• Jeśli kluczowy element jest mniejszy niż jego poprzednik, porównaj go z elementami wcześniejszymi. Przesuń większe elementy o jedną pozycję w górę, aby zrobić miejsce na zamieniony element.

Ilustracja:

# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 i klucz < arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i]) 

 5 6 11 12 13 

Złożoność czasowa: NA ² ))

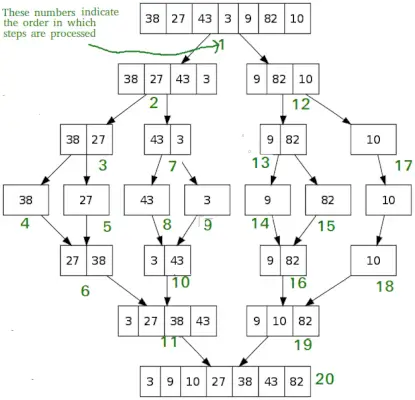
Sortowanie przez scalanie

Podobnie jak szybkie sortowanie, Sortowanie przez scalanie jest algorytmem Dziel i Rządź. Dzieli tablicę wejściową na dwie połowy, wywołuje siebie dla obu połówek, a następnie łączy dwie posortowane połówki. Funkcja merge() służy do łączenia dwóch połówek. Funkcja merge(arr, l, m, r) to kluczowy proces, który zakłada, że ​​arr[l..m] i arr[m+1..r] są posortowane i łączy dwie posortowane podtablice w jedną.

MergeSort(arr[], l, r) If r>l 1. Znajdź środkowy punkt, aby podzielić tablicę na dwie połowy: środek m = l+ (r-l)/2 2. Wywołaj mergeSort dla pierwszej połowy: Wywołaj mergeSort(arr, l, m) 3. Wywołaj mergeSort dla drugiej połowy: Wywołaj mergeSort(arr, m+1, r) 4. Połącz dwie połówki posortowane w kroku 2 i 3: Wywołaj merge(arr, l, m, r) 

# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Znajdowanie środka tablicy mid = len(arr)//2 # Dzielenie elementów tablicy L = arr[:mid] # na 2 połowy R = arr[mid:] # Sortowanie pierwszej połowy mergeSort(L) # Sortowanie drugiej połowy mergeSort(R) i = j = k = 0 # Kopiuj dane do tablic tymczasowych L[] i R[] podczas gdy i < len(L) and j  < len(R): if L[i]  < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i  < len(L): arr[k] = L[i] i += 1 k += 1 while j  < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr) 

Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13 

Złożoność czasowa: O(n(logn))

Szybkie sortowanie

Podobnie jak sortowanie przez scalanie, Szybkie sortowanie jest algorytmem Dziel i Rządź. Wybiera element jako element obrotowy i dzieli podaną tablicę wokół wybranego elementu obrotowego. Istnieje wiele różnych wersji narzędzia QuickSort, które wybierają przestaw na różne sposoby.

Zawsze wybieraj pierwszy element jako element obrotowy.

• Zawsze wybieraj ostatni element jako oś (zaimplementowano poniżej)
• Wybierz losowy element jako oś.
• Wybierz medianę jako oś obrotu.

Kluczowym procesem w QuickSort jest partycja(). Celem partycji jest, mając tablicę i element x tablicy jako oś obrotu, umieść x we ​​właściwej pozycji w posortowanej tablicy i umieść wszystkie mniejsze elementy (mniejsze niż x) przed x i umieść wszystkie większe elementy (większe niż x) po X. Wszystko to powinno odbywać się w czasie liniowym.

/* low -->Indeks początkowy, wysoki --> Indeks końcowy */ QuickSort(arr[], niski, wysoki) { if (low { /* pi to indeks partycjonowania, arr[pi] jest teraz na właściwym miejscu */ pi = partycja(arr, niski, wysoki); QuickSort(arr, low, pi - 1); // Przed pi QuickSort(arr, pi + 1, wysoki); // Po pi } } 

Algorytm partycji

Istnieje wiele sposobów podziału, poniżej pseudo kod przyjmuje metodę podaną w książce CLRS. Logika jest prosta, zaczynamy od skrajnego lewego elementu i śledzimy indeks mniejszych (lub równych) elementów, jak np. Jeśli podczas przechodzenia znajdziemy mniejszy element, zamieniamy bieżący element na arr[i]. W przeciwnym razie ignorujemy bieżący element.

/* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ partition (arr[], low, high) {  // pivot (Element to be placed at right position)  pivot = arr[high];   i = (low – 1) // Index of smaller element and indicates the   // right position of pivot found so far  for (j = low; j  <= high- 1; j++){  // If current element is smaller than the pivot  if (arr[j]   i++; // increment index of smaller element  swap arr[i] and arr[j]  }  }  swap arr[i + 1] and arr[high])  return (i + 1) } 

# Python3 implementation of QuickSort # This Function handles sorting part of quick sort # start and end points to first and last element of # an array respectively def partition(start, end, array): # Initializing pivot's index to start pivot_index = start pivot = array[pivot_index] # This loop runs till start pointer crosses # end pointer, and when it does we swap the # pivot with element on end pointer while start  < end: # Increment the start pointer till it finds an # element greater than pivot while start  < len(array) and array[start]  <= pivot: start += 1 # Decrement the end pointer till it finds an # element less than pivot while array[end]>obrót: end -= 1 # Jeśli początek i koniec nie przecinają się, # zamień liczby na początku i końcu if(start < end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start  < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}') 

Sorted array: [1, 5, 7, 8, 9, 10] 

Złożoność czasowa: O(n(logn))

Sortowanie powłoki

Sortowanie powłoki jest głównie odmianą sortowania przez wstawianie. Podczas sortowania przez wstawianie przesuwamy elementy tylko o jedną pozycję do przodu. Kiedy element musi zostać przesunięty daleko do przodu, wymaga to wielu ruchów. Ideą powłoki ShellSort jest umożliwienie wymiany odległych elementów. W ShellSort sortujemy tablicę h dla dużej wartości h. Zmniejszamy wartość h, aż osiągnie wartość 1. Mówi się, że tablica jest posortowana h, jeśli wszystkie podlisty każdej h ^t element jest posortowany.

# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = przerwa # sprawdza tablicę od lewej do prawej # aż do ostatniego możliwego indeksu j póki j < len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # teraz patrzymy wstecz od i-tego indeksu w lewo # zamieniamy wartości, które nie są we właściwej kolejności. k = i podczas gdy k - przerwa> -1: jeśli arr[k - przerwa]> arr[k]: arr[k-przerwa],arr[k] = arr[k],arr[k-przerwa] k -= 1 przerwa //= 2 # sterownik do sprawdzania kodu arr2 = [12, 34, 54, 2, 3] print('tablica wejściowa:',arr2) ShellSort(arr2) print('posortowana tablica', tablica2) 

input array: [12, 34, 54, 2, 3] sorted array [2, 3, 12, 34, 54] 

Złożoność czasowa: NA ² ).