WPROWADZENIE B-TREE - TECHCODEVIEW.COM

Ograniczenia tradycyjnych drzew wyszukiwania binarnego mogą być frustrujące. Poznaj B-Tree, wszechstronną strukturę danych, która z łatwością radzi sobie z ogromnymi ilościami danych. Jeśli chodzi o przechowywanie i przeszukiwanie dużych ilości danych, tradycyjne drzewa wyszukiwania binarnego mogą stać się niepraktyczne ze względu na ich słabą wydajność i duże zużycie pamięci. B-Trees, znane również jako B-Tree lub Balanced Tree, to rodzaj samobalansującego drzewa, które zostało specjalnie zaprojektowane, aby pokonać te ograniczenia.

W przeciwieństwie do tradycyjnych drzew wyszukiwania binarnego, drzewa B charakteryzują się dużą liczbą kluczy, które mogą przechowywać w jednym węźle, dlatego nazywane są również dużymi drzewami kluczy. Każdy węzeł w drzewie B może zawierać wiele kluczy, co pozwala na to, aby drzewo miało większy współczynnik rozgałęzienia, a tym samym mniejszą wysokość. Ta niewielka wysokość prowadzi do mniejszej liczby operacji we/wy dysku, co skutkuje szybszymi operacjami wyszukiwania i wstawiania. B-Drzewa szczególnie dobrze nadają się do systemów pamięci masowej, które mają powolny i nieporęczny dostęp do danych, takich jak dyski twarde, pamięć flash i dyski CD-ROM.

B-Trees utrzymuje równowagę, zapewniając, że każdy węzeł ma minimalną liczbę kluczy, dzięki czemu drzewo jest zawsze zrównoważone. Bilans ten gwarantuje, że złożoność czasowa operacji takich jak wstawianie, usuwanie i wyszukiwanie wynosi zawsze O(log n), niezależnie od początkowego kształtu drzewa.

Złożoność czasowa drzewa B:

Pan Nie.	Algorytm	Złożoność czasu
1.	Szukaj	O(log n)
2.	Wstawić	O(log n)
3.	Usuwać	O(log n)

Notatka: n jest całkowitą liczbą elementów w drzewie B

Właściwości B-Tree:

Wszystkie liście są na tym samym poziomie.
B-Tree definiuje się mianem minimalnego stopnia „ T „. Wartość ' T ' zależy od rozmiaru bloku dysku.
Każdy węzeł z wyjątkiem korzenia musi zawierać co najmniej klucze t-1. Korzeń może zawierać min 1 klucz.
Wszystkie węzły (łącznie z korzeniem) mogą zawierać co najwyżej ( 2*t – 1 ) Klucze.
Liczba dzieci węzła jest równa liczbie kluczy w nim plus 1 .
Wszystkie klucze węzła są sortowane w kolejności rosnącej. Dziecko między dwoma kluczami k1 I k2 zawiera wszystkie klucze z zakresu od k1 I k2 .
B-Tree rośnie i kurczy się od korzenia, w przeciwieństwie do drzewa wyszukiwania binarnego. Drzewa wyszukiwania binarnego rosną w dół, a także kurczą się w dół.
Podobnie jak w przypadku innych zrównoważonych drzew wyszukiwania binarnego, złożoność czasowa wyszukiwania, wstawiania i usuwania wynosi O (log n).
Wstawienie węzła do B-drzewa następuje tylko w węźle liścia.

Poniżej znajduje się przykład drzewa B o minimalnym rzędzie 5
Notatka: że w praktycznych drzewach B wartość minimalnego zamówienia jest znacznie większa niż 5.

Na powyższym diagramie widzimy, że wszystkie węzły-liście są na tym samym poziomie, a wszystkie nie-liście nie mają pustego poddrzewa i mają klucze o jeden mniej niż liczba ich dzieci.

Ciekawe fakty na temat drzew B:

Minimalna wysokość drzewa B, które może istnieć z n liczbą węzłów, a m jest maksymalną liczbą dzieci, jakie może mieć węzeł, wynosi: $h_{min} =lceillog_m (n + 1) ceil - 1$

Maksymalna wysokość drzewa B, które może istnieć z n liczbą węzłów, a t jest minimalną liczbą dzieci, jaką może mieć węzeł inny niż główny, wynosi: $h_{max} =lfloorlog_tfrac {n + 1}{2} floor$ I $t = lceilfrac {m}{2} ceil$

Przechodzenie w drzewie B:

Przechodzenie jest również podobne do przechodzenia Inorder w drzewie binarnym. Zaczynamy od lewego dziecka, rekurencyjnie drukujemy skrajne lewe dziecko, a następnie powtarzamy ten sam proces dla pozostałych dzieci i kluczy. Na koniec rekurencyjnie wydrukuj najbardziej prawe dziecko.

Operacja wyszukiwania w B-Tree:

Wyszukiwanie jest podobne do wyszukiwania w drzewie wyszukiwania binarnego. Niech poszukiwanym kluczem będzie k.

Zacznij od korzenia i rekurencyjnie przechodź w dół.
Dla każdego odwiedzonego węzła innego niż liść
- Jeśli węzeł ma klucz, po prostu zwracamy węzeł.
- W przeciwnym razie wracamy do odpowiedniego dziecka (dziecka, które znajduje się tuż przed pierwszym większym kluczem) węzła.
Jeśli dotrzemy do węzła liścia i nie znajdziemy k w węźle liścia, zwróć NULL.

Przeszukiwanie drzewa B jest podobne do przeszukiwania drzewa binarnego. Algorytm jest podobny i działa z rekurencją. Na każdym poziomie wyszukiwanie jest optymalizowane tak, jakby wartość klucza nie występowała w zakresie rodzica, to klucz znajdował się w innej gałęzi. Ponieważ wartości te ograniczają wyszukiwanie, są one również nazywane wartościami ograniczającymi lub wartościami separacji. Jeśli dotrzemy do węzła liścia i nie znajdziemy żądanego klucza, wyświetli się NULL.

Algorytm wyszukiwania elementu w drzewie B: -

C++

struct> Node {> > int> n;> > int> key[MAX_KEYS];> > Node* child[MAX_CHILDREN];> > bool> leaf;> };> Node* BtreeSearch(Node* x,> int> k) {> > int> i = 0;> > while> (i n && k>x->klawisz[i]) {> > i++;> > }> > if> (i n && k == x->klawisz[i]) {> > return> x;> > }> > if> (x->liść) {> > return> nullptr;> > }> > return> BtreeSearch(x->dziecko[i], k);> }>

C

BtreeSearch(x, k)> > i = 1> > > // n[x] means number of keys in x node> > while> i ? n[x] and k ? keyi[x]> > do> i = i + 1> > if> i n[x] and k = keyi[x]> > then> return> (x, i)> > if> leaf [x]> > then> return> NIL> > else> > return> BtreeSearch(ci[x], k)>

Jawa

class> Node {> > int> n;> > int> [] key => new> int> [MAX_KEYS];> > Node[] child => new> Node[MAX_CHILDREN];> > boolean> leaf;> }> Node BtreeSearch(Node x,> int> k) {> > int> i => 0> ;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }>

Python3

class> Node:> > def> __init__(> self> ):> > self> .n> => 0> > self> .key> => [> 0> ]> *> MAX_KEYS> > self> .child> => [> None> ]> *> MAX_CHILDREN> > self> .leaf> => True> def> BtreeSearch(x, k):> > i> => 0> > while>

i and k>= x.key[i]: i += 1 jeśli i oraz k == x.key[i]: return x jeśli x.leaf: return Brak return BtreeSearch(x.child[i], k)>

C#

class> Node {> > public> int> n;> > public> int> [] key => new> int> [MAX_KEYS];> > public> Node[] child => new> Node[MAX_CHILDREN];> > public> bool> leaf;> }> Node BtreeSearch(Node x,> int> k) {> > int> i = 0;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }>

JavaScript

// Define a Node class with properties n, key, child, and leaf> class Node {> > constructor() {> > this> .n = 0;> > this> .key => new> Array(MAX_KEYS);> > this> .child => new> Array(MAX_CHILDREN);> > this> .leaf => false> ;> > }> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> > let i = 0;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }>

Przykłady:

Wejście: Wyszukaj 120 w danym drzewie B.

Rozwiązanie:

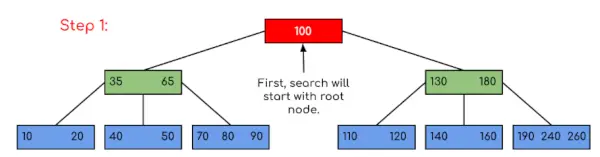
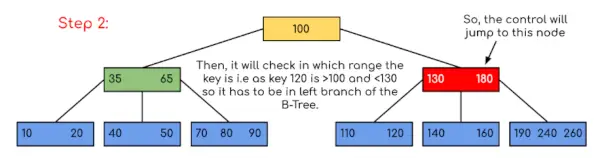
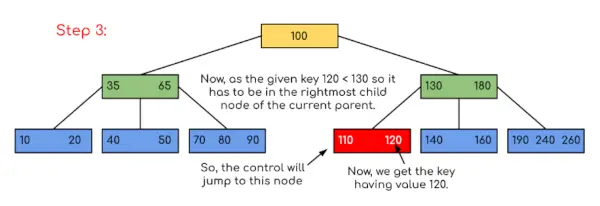
W tym przykładzie widzimy, że nasze wyszukiwanie zostało ograniczone poprzez ograniczenie szans na obecność klucza zawierającego wartość. Podobnie, jeśli w powyższym przykładzie będziemy musieli szukać 180, kontrola zatrzyma się w kroku 2, ponieważ program stwierdzi, że klucz 180 jest obecny w bieżącym węźle. I podobnie, jeśli ma wyszukać 90, to jako 90 <100, więc automatycznie przejdzie do lewego poddrzewa, a zatem przepływ sterowania będzie przebiegał podobnie jak pokazano w powyższym przykładzie.

Poniżej implementacja powyższego podejścia:

C++

// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> > int> * keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode** C;> // An array of child pointers> > int> n;> // Current number of keys> > bool> leaf;> // Is true when node is leaf. Otherwise false> public> :> > BTreeNode(> int> _t,> bool> _leaf);> // Constructor> > // A function to traverse all nodes in a subtree rooted> > // with this node> > void> traverse();> > // A function to search a key in the subtree rooted with> > // this node.> > BTreeNode*> > search(> int> k);> // returns NULL if k is not present.> > // Make the BTree friend of this so that we can access> > // private members of this class in BTree functions> > friend> class> BTree;> };> // A BTree> class> BTree {> > BTreeNode* root;> // Pointer to root node> > int> t;> // Minimum degree> public> :> > // Constructor (Initializes tree as empty)> > BTree(> int> _t)> > {> > root = NULL;> > t = _t;> > }> > // function to traverse the tree> > void> traverse()> > {> > if> (root != NULL)> > root->przemierzać();> > }> > // function to search a key in this tree> > BTreeNode* search(> int> k)> > {> > return> (root == NULL) ? NULL : root->szukaj(k);> > }> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(> int> _t,> bool> _leaf)> {> > // Copy the given minimum degree and leaf property> > t = _t;> > leaf = _leaf;> > // Allocate memory for maximum number of possible keys> > // and child pointers> > keys => new> int> [2 * t - 1];> > C => new> BTreeNode*[2 * t];> > // Initialize the number of keys as 0> > n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> > // There are n keys and n+1 children, traverse through n> > // keys and first n children> > int> i;> > for>

(i = 0; i   // If this is not leaf, then before printing key[i],  // traverse the subtree rooted with child C[i].  if (leaf == false)  C[i]->trawers();  cout < < ' '  < < keys[i];  }  // Print the subtree rooted with last child  if (leaf == false)  C[i]->trawers(); } // Funkcja przeszukująca klucz k w poddrzewie zakorzenionym w tym węźle BTreeNode* BTreeNode::search(int k) { // Znajdź pierwszy klucz większy lub równy k int i = 0;  podczas gdy (i klawisze [i]) i++;  // Jeśli znaleziony klucz jest równy k, zwróć ten węzeł if (keys[i] == k) zwróć to;  // Jeśli nie znaleziono tutaj klucza i jest to węzeł liścia if (leaf == true) return NULL;  // Przejdź do odpowiedniego dziecka return C[i]->search(k); }>

Jawa

// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> > public> BTreeNode root;> // Pointer to root node> > public> int> t;> // Minimum degree> > // Constructor (Initializes tree as empty)> > Btree(> int> t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > // function to traverse the tree> > public> void> traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > System.out.println();> > }> > // function to search a key in this tree> > public> BTreeNode search(> int> k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> }> // A BTree node> class> BTreeNode {> > int> [] keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode[] C;> // An array of child pointers> > int> n;> // Current number of keys> > boolean> > leaf;> // Is true when node is leaf. Otherwise false> > // Constructor> > BTreeNode(> int> t,> boolean> leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> int> [> 2> * t -> 1> ];> > this> .C => new> BTreeNode[> 2> * t];> > this> .n => 0> ;> > }> > // A function to traverse all nodes in a subtree rooted> > // with this node> > public> void> traverse()> > {> > // There are n keys and n+1 children, traverse> > // through n keys and first n children> > int> i => 0> ;> > for> (i => 0> ; i <> this> .n; i++) {> > // If this is not leaf, then before printing> > // key[i], traverse the subtree rooted with> > // child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > System.out.print(keys[i] +> ' '> );> > }> > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > // A function to search a key in the subtree rooted with> > // this node.> > BTreeNode search(> int> k)> > {> // returns NULL if k is not present.> > // Find the first key greater than or equal to k> > int> i => 0> ;> > while> (i keys[i])> > i++;> > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > // If the key is not found here and this is a leaf> > // node> > if> (leaf ==> true> )> > return> null> ;> > // Go to the appropriate child> > return> C[i].search(k);> > }> }>

Python3

# Create a node> class> BTreeNode:> > def> __init__(> self> , leaf> => False> ):> > self> .leaf> => leaf> > self> .keys> => []> > self> .child> => []> # Tree> class> BTree:> > def> __init__(> self> , t):> > self> .root> => BTreeNode(> True> )> > self> .t> => t> > # Insert node> > def> insert(> self> , k):> > root> => self> .root> > if> len> (root.keys)> => => (> 2> *> self> .t)> -> 1> :> > temp> => BTreeNode()> > self> .root> => temp> > temp.child.insert(> 0> , root)> > self> .split_child(temp,> 0> )> > self> .insert_non_full(temp, k)> > else> :> > self> .insert_non_full(root, k)> > # Insert nonfull> > def> insert_non_full(> self> , x, k):> > i> => len> (x.keys)> -> 1> > if> x.leaf:> > x.keys.append((> None> ,> None> ))> > while> i>> => 0> and> k[> 0>

] 0]:  x.keys[i + 1] = x.keys[i]  i -= 1  x.keys[i + 1] = k  else:  while i>= 0 i k[0] 0]: i -= 1 i += 1 if len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Podziel dziecko def split_child(self, x, i): t = self .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1] jeśli nie y.leaf: z.child = y.child[t: 2 * t] y. child = y.child[0: t - 1] # Wydrukuj drzewo def print_tree(self, x, l=0): print('Poziom ', l, ' ', len(x.keys), end=':') dla i w x.keys: print(i, end=' ') print() l += 1 if len(x.child)> 0: dla i w x.child: self.print_tree(i, l) # Klucz wyszukiwania w drzewie def search_key(self, k, x=None): jeśli x nie jest Brak: i = 0 podczas gdy i x.keys[i][0]: i += 1 jeśli i

C#

// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> > public> BTreeNode root;> // Pointer to root node> > public> int> t;> // Minimum degree> > // Constructor (Initializes tree as empty)> > Btree(> int> t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > // function to traverse the tree> > public> void> traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > Console.WriteLine();> > }> > // function to search a key in this tree> > public> BTreeNode search(> int> k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> }> // A BTree node> class> BTreeNode {> > int> [] keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode[] C;> // An array of child pointers> > int> n;> // Current number of keys> > bool> leaf;> // Is true when node is leaf. Otherwise false> > // Constructor> > BTreeNode(> int> t,> bool> leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> int> [2 * t - 1];> > this> .C => new> BTreeNode[2 * t];> > this> .n = 0;> > }> > // A function to traverse all nodes in a subtree rooted> > // with this node> > public> void> traverse()> > {> > // There are n keys and n+1 children, traverse> > // through n keys and first n children> > int> i = 0;> > for> (i = 0; i <> this> .n; i++) {> > // If this is not leaf, then before printing> > // key[i], traverse the subtree rooted with> > // child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > Console.Write(keys[i] +> ' '> );> > }> > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > // A function to search a key in the subtree rooted with> > // this node.> > public> BTreeNode search(> int> k)> > {> // returns NULL if k is not present.> > // Find the first key greater than or equal to k> > int> i = 0;> > while> (i keys[i])> > i++;> > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > // If the key is not found here and this is a leaf> > // node> > if> (leaf ==> true> )> > return> null> ;> > // Go to the appropriate child> > return> C[i].search(k);> > }> }> // This code is contributed by Rajput-Ji>

JavaScript

// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> > // Constructor (Initializes tree as empty)> > constructor(t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > > // function to traverse the tree> > traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > document.write(> ' '> );> > }> > > // function to search a key in this tree> > search(k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> > }> // A BTree node> class BTreeNode> {> > // Constructor> > constructor(t,leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> Array(2 * t - 1);> > this> .C => new> Array(2 * t);> > this> .n = 0;> > }> > // A function to traverse all nodes in a subtree rooted with this node> > traverse()> > {> > // There are n keys and n+1 children, traverse through n keys> > // and first n children> > let i = 0;> > for> (i = 0; i <> this> .n; i++) {> > > // If this is not leaf, then before printing key[i],> > // traverse the subtree rooted with child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > document.write(keys[i] +> ' '> );> > }> > > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > > // A function to search a key in the subtree rooted with this node.> > search(k)> // returns NULL if k is not present.> > {> > > // Find the first key greater than or equal to k> > let i = 0;> > while> (i keys[i])> > i++;> > > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > > // If the key is not found here and this is a leaf node> > if> (leaf ==> true> )> > return> null> ;> > > // Go to the appropriate child> > return> C[i].search(k);> > }> }> // This code is contributed by patel2127>

Notatka: Powyższy kod nie zawiera programu sterownika. Cały program omówimy w następnym poście na temat Wstawienie drzewa B .

Istnieją dwie konwencje definiowania drzewa B, jedna polega na określeniu minimalnego stopnia, druga polega na zdefiniowaniu kolejności. Przestrzegaliśmy konwencji dotyczącej minimalnego stopnia naukowego i będziemy się nią kierować w kolejnych postach na B-Tree. Nazwy zmiennych użyte w powyższym programie również pozostają takie same

Zastosowania drzew B:

Stosowany jest w dużych bazach danych w celu uzyskania dostępu do danych przechowywanych na dysku
Wyszukiwanie danych w zbiorze danych można osiągnąć w znacznie krótszym czasie przy użyciu B-Tree
Dzięki funkcji indeksowania można osiągnąć indeksowanie wielopoziomowe.
Większość serwerów również korzysta z podejścia B-tree.
B-Drzewa są używane w systemach CAD do organizowania i wyszukiwania danych geometrycznych.
Drzewa B są również wykorzystywane w innych obszarach, takich jak przetwarzanie języka naturalnego, sieci komputerowe i kryptografia.

Zalety drzew B:

Drzewa B mają gwarantowaną złożoność czasową O(log n) dla podstawowych operacji, takich jak wstawianie, usuwanie i wyszukiwanie, co czyni je odpowiednimi dla dużych zbiorów danych i aplikacji czasu rzeczywistego.
B-Drzewa są samobalansujące.
Wysoka współbieżność i wysoka przepustowość.
Efektywne wykorzystanie pamięci.

Wady drzew B:

B-Drzewa opierają się na dyskowych strukturach danych i mogą powodować duże wykorzystanie dysku.
Nie jest to najlepsze rozwiązanie we wszystkich przypadkach.
Powolny w porównaniu do innych struktur danych.

Wstawianie i usuwanie:
Wstawienie drzewa B
Usuwanie drzewa B