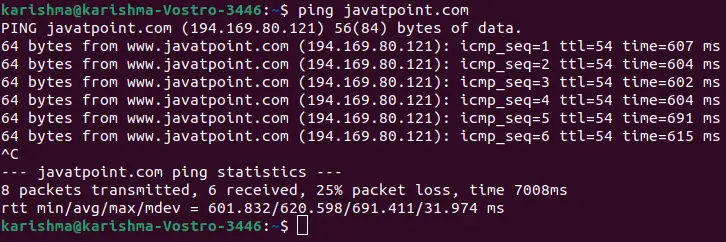
Głębokość pierwszego wyszukiwania lub DFS dla wykresu

Pierwsze przejście na głębokość (lub DFS) ponieważ wykres jest podobny do Głębokość Pierwsze przejście drzewa. Jedynym haczykiem jest to, że w przeciwieństwie do drzew, grafy mogą zawierać cykle (węzeł można odwiedzić dwukrotnie). Aby uniknąć wielokrotnego przetwarzania węzła, użyj odwiedzanej tablicy logicznej. Wykres może mieć więcej niż jedno przejście DFS.
Przykład:
Zalecana praktyka DFS wykresu Wypróbuj!Wejście: n = 4, e = 6
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3
Wyjście: DFS z wierzchołka 1 : 1 2 0 3
Wyjaśnienie:
Schemat DFS:
Przykład 1
Wejście: n = 4, mi = 6
2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3
Wyjście: DFS z wierzchołka 2 : 2 0 1 3
Wyjaśnienie:
Schemat DFS:
Przykład 2
Jak działa DFS?
Przeszukiwanie w głąb to algorytm służący do przechodzenia lub przeszukiwania struktur danych w postaci drzew lub grafów. Algorytm rozpoczyna się od węzła głównego (wybierając dowolny węzeł jako węzeł główny w przypadku wykresu) i bada możliwie najdalej każdą gałąź przed cofnięciem się.
Pozwól nam zrozumieć działanie Pierwsze wyszukiwanie w głębi za pomocą poniższej ilustracji:
Krok 1: Początkowo stos i odwiedzane tablice są puste.
Stos i odwiedzane tablice są początkowo puste.
Krok 2: Odwiedź 0 i umieść na stosie sąsiadujące z nim węzły, które nie zostały jeszcze odwiedzone.
Odwiedź węzeł 0 i umieść sąsiadujące z nim węzły (1, 2, 3) na stosie
Krok 3: Teraz węzeł 1 jest na górze stosu, więc odwiedź węzeł 1, zdejmij go ze stosu i umieść na stosie wszystkie sąsiednie węzły, które nie są odwiedzane.
Odwiedź węzeł 1
Krok 4: Teraz, Węzeł 2 na górze stosu, więc odwiedź węzeł 2, zdejmij go ze stosu i umieść na stosie wszystkie sąsiednie węzły, które nie są odwiedzane (tj. 3, 4).
Odwiedź węzeł 2 i umieść jego nieodwiedzone sąsiednie węzły (3, 4) na stosie
Krok 5: Teraz węzeł 4 na szczycie stosu, więc odwiedź węzeł 4, zdejmij go ze stosu i umieść na stosie wszystkie sąsiednie węzły, które nie są odwiedzane.
Odwiedź węzeł 4
Krok 6: Teraz węzeł 3 znajduje się na szczycie stosu, więc odwiedź węzeł 3, zdejmij go ze stosu i umieść na stosie wszystkie sąsiednie węzły, które nie są odwiedzane.
Odwiedź węzeł 3
Teraz Stack staje się pusty, co oznacza, że odwiedziliśmy wszystkie węzły i nasza podróż DFS dobiegła końca.
Poniżej implementacja powyższego podejścia:
C++
// C++ program to print DFS traversal from> // a given vertex in a given graph> #include> using> namespace> std;> // Graph class represents a directed graph> // using adjacency list representation> class> Graph {> public> :> > map <> int> ,> bool> >odwiedziłem;> > map <> int> , list <> int> >> przym;> > // Function to add an edge to graph> > void> addEdge(> int> v,> int> w);> > // DFS traversal of the vertices> > // reachable from v> > void> DFS(> int> v);> };> void> Graph::addEdge(> int> v,> int> w)> {> > // Add w to v’s list.> > adj[v].push_back(w);> }> void> Graph::DFS(> int> v)> {> > // Mark the current node as visited and> > // print it> > visited[v] => true> ;> > cout < < v < <> ' '> ;> > // Recur for all the vertices adjacent> > // to this vertex> > list <> int> >::iterator i;> > for> (i = adj[v].begin(); i != adj[v].end(); ++i)> > if> (!visited[*i])> > DFS(*i);> }> // Driver code> int> main()> {> > // Create a graph given in the above diagram> > Graph g;> > g.addEdge(0, 1);> > g.addEdge(0, 2);> > g.addEdge(1, 2);> > g.addEdge(2, 0);> > g.addEdge(2, 3);> > g.addEdge(3, 3);> > cout < <> 'Following is Depth First Traversal'> > ' (starting from vertex 2)
'> ;> > // Function call> > g.DFS(2);> > return> 0;> }> // improved by Vishnudev C> |
Jawa
// Java program to print DFS traversal> // from a given graph> import> java.io.*;> import> java.util.*;> // This class represents a> // directed graph using adjacency> // list representation> class> Graph {> > private> int> V;> > // Array of lists for> > // Adjacency List Representation> > private> LinkedList adj[];> > // Constructor> > @SuppressWarnings> (> 'unchecked'> ) Graph(> int> v)> > {> > V = v;> > adj => new> LinkedList[v];> > for> (> int> i => 0> ; i adj[i] = new LinkedList(); } // Function to add an edge into the graph void addEdge(int v, int w) { // Add w to v's list. adj[v].add(w); } // A function used by DFS void DFSUtil(int v, boolean visited[]) { // Mark the current node as visited and print it visited[v] = true; System.out.print(v + ' '); // Recur for all the vertices adjacent to this // vertex Iterator i = adj[v].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) DFSUtil(n, visited); } } // The function to do DFS traversal. // It uses recursive DFSUtil() void DFS(int v) { // Mark all the vertices as // not visited(set as // false by default in java) boolean visited[] = new boolean[V]; // Call the recursive helper // function to print DFS // traversal DFSUtil(v, visited); } // Driver Code public static void main(String args[]) { Graph g = new Graph(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); g.addEdge(3, 3); System.out.println( 'Following is Depth First Traversal ' + '(starting from vertex 2)'); // Function call g.DFS(2); } } // This code is contributed by Aakash Hasija> |
Python3
# Python3 program to print DFS traversal> # from a given graph> from> collections> import> defaultdict> # This class represents a directed graph using> # adjacency list representation> class> Graph:> > # Constructor> > def> __init__(> self> ):> > # Default dictionary to store graph> > self> .graph> => defaultdict(> list> )> > > # Function to add an edge to graph> > def> addEdge(> self> , u, v):> > self> .graph[u].append(v)> > > # A function used by DFS> > def> DFSUtil(> self> , v, visited):> > # Mark the current node as visited> > # and print it> > visited.add(v)> > print> (v, end> => ' '> )> > # Recur for all the vertices> > # adjacent to this vertex> > for> neighbour> in> self> .graph[v]:> > if> neighbour> not> in> visited:> > self> .DFSUtil(neighbour, visited)> > > # The function to do DFS traversal. It uses> > # recursive DFSUtil()> > def> DFS(> self> , v):> > # Create a set to store visited vertices> > visited> => set> ()> > # Call the recursive helper function> > # to print DFS traversal> > self> .DFSUtil(v, visited)> # Driver's code> if> __name__> => => '__main__'> :> > g> => Graph()> > g.addEdge(> 0> ,> 1> )> > g.addEdge(> 0> ,> 2> )> > g.addEdge(> 1> ,> 2> )> > g.addEdge(> 2> ,> 0> )> > g.addEdge(> 2> ,> 3> )> > g.addEdge(> 3> ,> 3> )> > print> (> 'Following is Depth First Traversal (starting from vertex 2)'> )> > > # Function call> > g.DFS(> 2> )> # This code is contributed by Neelam Yadav> |
C#
// C# program to print DFS traversal> // from a given graph> using> System;> using> System.Collections.Generic;> // This class represents a directed graph> // using adjacency list representation> class> Graph {> > private> int> V;> > // Array of lists for> > // Adjacency List Representation> > private> List <> int> >[] przym;> > // Constructor> > Graph(> int> v)> > {> > V = v;> > adj => new> List <> int> >[w ];> > for> (> int> i = 0; i adj[i] = new List |
JavaScript
// Javascript program to print DFS> // traversal from a given> // graph> // This class represents a> // directed graph using adjacency> // list representation> class Graph> {> > > // Constructor> > constructor(v)> > {> > this> .V = v;> > this> .adj => new> Array(v);> > for> (let i = 0; i this.adj[i] = []; } // Function to add an edge into the graph addEdge(v, w) { // Add w to v's list. this.adj[v].push(w); } // A function used by DFS DFSUtil(v, visited) { // Mark the current node as visited and print it visited[v] = true; console.log(v + ' '); // Recur for all the vertices adjacent to this // vertex for(let i of this.adj[v].values()) { let n = i if (!visited[n]) this.DFSUtil(n, visited); } } // The function to do DFS traversal. // It uses recursive // DFSUtil() DFS(v) { // Mark all the vertices as // not visited(set as // false by default in java) let visited = new Array(this.V); for(let i = 0; i |
Wyjście
Following is Depth First Traversal (starting from vertex 2) 2 0 1 3
Analiza złożoności pierwszego wyszukiwania wgłębnego:
- Złożoność czasowa: O(V + E), gdzie V to liczba wierzchołków, a E to liczba krawędzi grafu.
- Przestrzeń pomocnicza: O(V + E), ponieważ wymagana jest dodatkowa odwiedzana tablica o rozmiarze V, oraz rozmiar stosu dla iteracyjnego wywołania funkcji DFS.