Modèle de phyllotaxie en Python | Une unité de Botanique Algorithmique

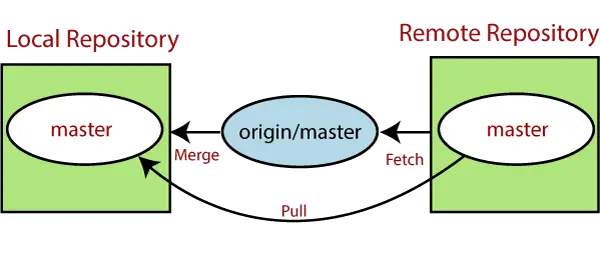
La phyllotaxie/phyllotaxie est la disposition des feuilles sur une tige de plante et les spirales phyllotactiques forment une classe distinctive de motifs dans la nature. Le mot lui-même vient du grec phullon signifiant « feuille » et taxis signifiant « arrangement ». Les arrangements floraux phyllotaxiques de base comprennent :
1. Phyllotaxie en spirale -
Dans la phyllotaxie spirale, les organes floraux individuels sont créés dans un intervalle de temps régulier avec le même angle divergent. L'angle divergent dans une fleur à phyllotaxie spirale est d'environ 137,5 degrés, ce qui indique un motif qui suit un
Série de Fibonacci
L'image ci-dessous montre les modèles de phyllotaxie en spirale ayant des modèles en spirale dans le sens des aiguilles d'une montre et dans le sens inverse des aiguilles d'une montre.

Points importants à noter :
- Les séries de Fibonacci décrivent généralement les spirales trouvées dans la nature. Il est calculé comme une série où la paire de nombres précédente correspond au nombre suivant de la série. La série est 1 1 2 3 5 8 13 21 34 55 89… .
- Il existe en fait un jeu de spirales dans le sens des aiguilles d’une montre et un autre dans le sens inverse des aiguilles d’une montre.
- Les spirales d'organes floraux suivent un ensemble de numérateur et de dénominateur de nombres de Fibonacci décalés (1/2 1/3 2/5 3/8 5/13 8/21 13/34…). Le numérateur est le nombre de fois ou de tours autour de l'axe pour revenir à l'origine d'initiation. Le dénominateur indique le nombre d'organes initiés lors des tours. Donc un 2/5 indiquerait 2 tours autour de l'axe et 5 organes pour revenir à l'origine.
- ex - Chez le pin nous avons (2 3) (5 3) et (5 8) phyllotaxes en capituli les paires trouvées sont (21 34) (55 34) (55 89) et (89 144) et sur les ananas à écailles hexagonales les triplets (8 13 21) ou (13 21 34) se retrouvent selon la taille des spécimens.
- La prévalence de la séquence de Fibonacci dans la phyllotaxie est souvent appelée « le mystère de la phyllotaxie ».
D’autres types d’arrangements floraux phyllotaxiques sont :
2. Phyllotaxie verticillée 3. Phyllotaxie verticillée simple 4. Phyllotaxie verticillée complexe et 5. Phyllotaxie irrégulière
Formation du motif : résumé
La belle disposition des feuilles de certaines plantes appelées phyllotaxie obéit à un certain nombre de relations mathématiques subtiles. Par exemple, les fleurons de la tête d'un tournesol forment deux spirales dirigées de manière opposée : 55 d'entre elles dans le sens des aiguilles d'une montre et 34 dans le sens inverse des aiguilles d'une montre. Étonnamment
- Ces nombres sont des nombres de Fibonacci consécutifs.
- Les rapports des nombres de Fibonacci alternatifs sont donnés par les convergents vers φ^(-2) où φ est le nombre d'or et on dit qu'ils mesurent la fraction de tour entre des feuilles successives sur la tige d'une plante :
- Ex : 1/2 pour l'orme et le tilleul 1/3 pour le hêtre et le noisetier 2/5 pour le chêne et le pommier 3/8 pour le peuplier et le rosier 5/13 pour le saule et l'amandier etc.
- Chaque nouvelle feuille d'une tige de plante est positionnée à un certain angle par rapport à la précédente et cet angle est constant entre les feuilles : généralement environ 137,5 degrés.
Autrement dit, si vous regardez la plante d'en haut et mesurez l'angle formé entre une ligne tracée de la tige à la feuille et une ligne correspondante pour la feuille suivante, vous constaterez qu'il existe généralement un angle fixe appelé angle de divergence. Ici, nous nous intéressons à la phyllotaxie en spirale et nous coderons pour former un motif de phyllotaxie en spirale en python à l'aide de graphiques de tortue.
Conception du code
- Nous coderons deux fonctions, l'une pour dessiner le motif de phyllotaxie et l'autre pour dessiner les pétales.
- Les pétales doivent être dessinés seulement une fois le motif phyllotaxis terminé. Nous appellerons donc la fonction drawPetal() depuis l'intérieur de la fonction drawPhyllPattern() avec les dernières coordonnées x et y visitées après avoir dessiné le motif Phyllotaxis.
- La fonction drawPetal() dessinera les pétales avec les fonctions et fonctionnalités de tortue, reportez-vous Programmation des tortues .
Pour coder le modèle de phyllotaxie, nous devons suivre ces équations :
x = r*cos(θ)
y = r*sin(θ)
r θ can also vary - so the to form phyllotactic pattern we substitutethe cartesian form
by polar form:
r = c*sqrt(n)
θ = n*137.508°
 Reduces the problem to optimal packing on a disc so
Reduces the problem to optimal packing on a disc so
r = c*sqrt(n) is from the area of the circle
Area = πr² and n fills the Area in some units
c1 * n/π = r² c is 1/sqrt(c1/π)
So r = some constant c * sqrt(n)
PseudoCode : modèle de phyllotaxie
IMPORT MODULES ( MATH TURTLE )
FUNCTION - DrawPhyllotaxisPattern( turtle t length petalstart angle = 137.508 size cspread)
turtleColor('Black')
FillColor(''Orange')
Convert angle to radians (Φ)
initialize ( xcenterycenter ) = ( 00 )
Drawing the Pattern Starts:
For n in Range ( 0t ):
r = cspread * sqrt(n)
θ = n * Φ
x = r * cos(θ) + xcenter
y = r * sin(θ) + ycenter
TURTLE POSITION(xy)
START DRAWING():
if Drawing pattern ends:
DrawFlowerPetals()
FUNCTION - DrawFlowerPetals(Turtle x coordinate y coordinate)
DRAW using Turtle methods
Create Turtle = gfg
Call DrawPhyllotaxisPattern( gfg t length petalstart angle = 137.508 size cspread)
END
Python Pattern APython Pattern Bimport math import turtle def drawPhyllPattern ( turtle t petalstart angle = 137.508 size = 2 cspread = 4 ): '''print a pattern of circles using spiral phyllotactic data''' # initialize position # turtle.pen(outline=1 pencolor='black' fillcolor='orange') turtle . color ( 'black' ) turtle . fillcolor ( 'orange' ) phi = angle * ( math . pi / 180.0 ) #we convert to radian xcenter = 0.0 ycenter = 0.0 # for loops iterate in this case from the first value until < 4 so for n in range ( 0 t ): r = cspread * math . sqrt ( n ) theta = n * phi x = r * math . cos ( theta ) + xcenter y = r * math . sin ( theta ) + ycenter # move the turtle to that position and draw turtle . up () turtle . setpos ( x y ) turtle . down () # orient the turtle correctly turtle . setheading ( n * angle ) if n > petalstart - 1 : turtle . color ( 'yellow' ) drawPetal ( turtle x y ) else : turtle . stamp () def drawPetal ( turtle x y ): turtle . penup () turtle . goto ( x y ) turtle . pendown () turtle . color ( 'black' ) turtle . fillcolor ( 'yellow' ) turtle . begin_fill () turtle . right ( 20 ) turtle . forward ( 70 ) turtle . left ( 40 ) turtle . forward ( 70 ) turtle . left ( 140 ) turtle . forward ( 70 ) turtle . left ( 40 ) turtle . forward ( 70 ) turtle . penup () turtle . end_fill () # this is needed to complete the last petal gfg = turtle . Turtle () gfg . shape ( 'turtle' ) gfg . speed ( 0 ) # make the turtle go as fast as possible drawPhyllPattern ( gfg 200 160 137.508 ) gfg . penup () gfg . forward ( 1000 )Sortir:
Modèles de phyllotaxie.

Créer un quiz