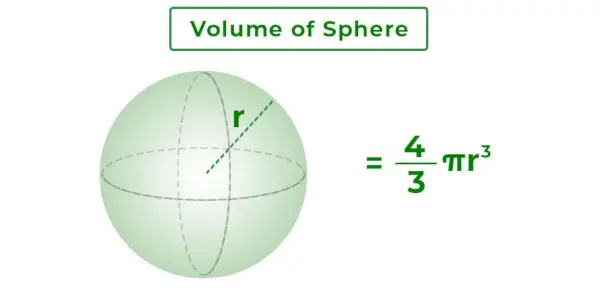
Volum av en sfære er mengden væske en kule kan inneholde. Formelen for volum av sfære er gitt som 4/3πr ³ . Det er rommet som okkuperes av en kule i 3-dimensjonalt rom. Det måles i enhet ³ dvs. m ³ , cm ³ , etc. En kule er et tredimensjonalt solid objekt med en rund form i geometri.

Volumet av sfæren er det totale rommet som okkuperes av sfærens overflate, og det er proporsjonalt med kuben av sfærens radius. I denne artikkelen vil vi lære om Volume of Sphere, Volume of Sphere Formula, Volume of Sphere Formula Eksempler og andre i detalj.

• Hva er volumet av en sfære?
• Volum av sfæreformel
• Volum av en solid sfære
• Volum av en hul sfære
• Volum av sfæreformelavledning
• Hvordan beregne volum av sfære?

Hva er volumet av en sfære?

Volum av en kule er mengden plass den tar opp i den. Kulen er en tredimensjonal rund solid form der alle punktene på overflaten er like fordelt fra midten. Den faste avstanden er sfærens radius, og det faste punktet er sfærens sentrum. Vi vil merke en endring i form når sirkelen snus. Som et resultat av rotasjonen av det todimensjonale objektet kjent som en sirkel, oppnås den tredimensjonale formen til en kule.

Lære mer,

• Kule
• Overflateareal av sfære

Volum av en sfære Definisjon

Volum av en sfære er den totale massen som er omsluttet av sfærens overflate. Det er 3D-rommet inne i sfæren. Det avhenger av sfærens radius. Bildet som er lagt til nedenfor viser en kule med radius r og volumet.

Volum av sfæreformel

Volum av sfæreformel er formelen som brukes til å finne volumet til sfæren når dens radius er gitt. Formelen for volumet av sfære for sfæren med radius R er lagt til nedenfor,

Volum av sfæreformel = 4/3πr ³

Hvor,

• r er radiusen til en kule
• Pi er en konstant og verdien er 22/7

En sfære er generelt kategorisert i to som er,

• Volum av solid sfære
• Volum av hul sfære

La oss lære om dem i detalj.

Volum av en solid sfære

En solid kule er en kule som er helt fylt til innsiden. dvs. den har masse til kjernen og formelen for volumet når radien er r er,

Volum av en solid kule(V) = (4/3)πr ³

Volum av en hul sfære

For en hul kule er dens indre rom tom og anta at dens ytre radius er det R og dens indre radius er r, deretter beregnes volumet ved hjelp av formelen,

Volum av hul sfære = (4/3)π(R ³ – r ³ )

Volum av sfæreformelavledning

Formel for volum av sfære kan utledes ved å bruke følgende metoder:

• Bruke integrasjon
• Bruke Archimedes forhold mellom sylinder, kjegle og sfære

La oss diskutere disse metodene i detalj som følger:

Volum av sfære som bruker integrasjon

Ved å bruke integrasjonstilnærmingen kan vi ganske enkelt beregne volumet til en kule.

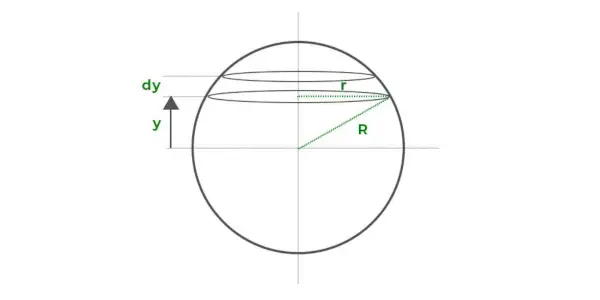
Anta at sfærens volum består av en serie tynne sirkulære skiver stablet oppå hverandre, som tegnet i diagrammet ovenfor. Hver tynn skive har en radius på r og en tykkelse på dy som er y avstand fra x-aksen.

La volumet på en plate være dV. Verdien av dV er gitt av,

dV = (πr ² ) deg

Dermed er dV = π (R ² - og ² ) deg

Det totale volumet av sfæren vil være summen av volumene til alle disse små skivene. Den nødvendige verdien kan oppnås ved å integrere uttrykket fra grense -R til R.

Så volumet av sfæren blir,

V = int_{y=-R}^{y=R} dV

⇒ V = int_{y=-R}^{y=R}π(R^2 – y^2)dy

⇒ V = pi|(R^2y – frac{y^3}{3})dy|_{y=-R}^{y=R}

⇒ V = pi left[R^3-frac{R^3}{3}-(-R^3+frac{R^3}{3}) ight]

⇒ V = pi left[2R^3-frac{2R^3}{3} ight]

⇒ V = frac{4}{3}pi R^3

Dermed er formelen for volum av kule utledet.

Volum av sfære ved hjelp av Archimedes-relasjoner

Som Arkimedes allerede har bevist, hvis en kjegle, en kule og en sylinder har samme radius r og samme høyde, er volumene deres i forholdet 1:2:3.

Derfor kan vi si:

Volum av sylinder = Volum av kjegle + Volum av sfære

Dermed volum av sfære = volum av sylinder - volum av kjegle

Som vi vet er volumet av sylinder = πr ² h og volum av kjegle = (1/3)πr ² h

Ved å erstatte disse verdiene i ligningen får vi:

Volum av sfære = πr ² h – (1/3)πr ² h = (2/3)πr ² h

Vi antar at høyden på sylinderen er lik diameteren på kulen, som er 2r. Dermed:

Volum av kule er (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³

Sjekk også

• Formel for sfærisk hettevolum
• Formel for sfærisk sektor
• Formel for sfærisk segment

Hvordan beregne volum av sfære?

Volum av sfære er plassen som okkuperes av en sfære. Volumet kan beregnes ved hjelp av formelen V = 4/3πr ³ .

Trinn som kreves for å beregne volumet til en kule er:

Trinn 1: Merk verdien av radiusen til kulen.

2. september: Finn kuben til radiusen.

Trinn 3: Multipliser kuben av radiusen med (4/3)π

Trinn 4: Legg til (enheten) ³ til det endelige svaret.

Eksempel for å beregne volum av sfære

Eksempel: Finn volumet til en kule med en radius på 7 cm.

Gitt, r = 7 cm

V = (4/3)πr ³

Volum av kule, V = ((4/3) × π × 7 ³ ) cm ³

Høyde = 1436,8 cm ³

Dermed er volumet av sfæren 1436,8 cm ³

Les mer

• Volum av kjegle
• Volum av kube
• Volum av sylinder

Volum av sfæreeksempler

Eksempel 1. Finn volumet til kulen hvis radius er 9 cm.

Løsning:

Vi har, r = 9

Volum av kule = 4/3 πr ³

⇒ Volum av sfære = (4/3) (3,14) (9) (9) (9)

⇒ Volum av kule = (4) (3.14) (3) (9) (9)

⇒ Volum av kule = 3052 cm ³

Eksempel 2. Finn volumet til kulen hvis radius er 12 cm.

Løsning:

Vi har r = 12

Volum av kule = 4/3 πr ³

⇒ Volum av sfære = (4/3) (3,14) (12) (12) (12)

⇒ Volum av kule = (4) (3.14) (4) (12) (12)

⇒ Volum av kule = 7234,56 cm ³

Eksempel 3. Finn volumet til kulen hvis radius er 6 cm.

Løsning:

Vi har r = 6

Volum av kule = 4/3 πr ³

⇒ Volum av sfære = (4/3) (3,14) (6) (6) (6)

⇒ Volum av kule = (4) (3.14) (2) (6) (6)

⇒ Volum av kule = 904,32 cm ³

Eksempel 4. Finn volumet til kulen hvis radius er 4 cm.

Løsning:

Vi har r = 4

Volum av kule = 4/3 πr3

⇒ Volum av kule = (4/3) (3,14) (4) (4) (4)

⇒ Volum av kule = (1,33) (3,14) (4) (4) (4)

⇒ Volum av kule = 267,27 cm ³

Eksempel 5. Finn volumet til kulen hvis diameter er 10 cm.

Løsning:

Vi har 2r = 10

⇒ r = 5

Volum av sfære = 4/3 πr ³

⇒ Volum av sfære = (4/3) (3,14) (5) (5) (5)

⇒ Volum av kule = (1,33) (3,14) (5) (5) (5)

⇒ Volum av kule = 522,025 cm ³

Eksempel 6. Finn volumet til kulen hvis diameter er 16 cm.

Løsning:

Vi har 2r = 16

⇒ r = 8

Volum av kule = 4/3 πr ³

⇒ Volum av kule = (4/3) (3,14) (8) (8) (8)

⇒ Volum av kule = (1,33) (3,14) (8) (8) (8)

⇒ Volum av kule = 2138,21 cm ³

Eksempel 7. Finn volumet til kulen hvis diameter er 14 cm.

Løsning:

Vi har 2r = 14

⇒ r = 7

Volum av kule = 4/3 πr ³

⇒ Volum av sfære = (4/3) (3,14) (7) (7) (7)

⇒ Volum av kule = (1,33) (3,14) (7) (7) (7)

⇒ Volum av kule = 1432,43 cm ³

Volum av sfære-praksisspørsmål

Q1: Finn volumet til kulen hvis diameter er 34 cm.

Q2: Finn volumet til den hule kulen hvis indre er 4 cm og ytre radius er 8 cm.

Q3: Finn volumet til kulen hvis radius er 14 cm.

Q4: Hva er volumet av en kule hvis radius er lik siden av kvadratet med arealet 144 m ² .

Volum av Sphere-vanlige spørsmål

Hva er Volume of Sphere?

Volum av sfære er plassen som okkuperes av sfærens overflate.

Hva er overflatearealet til en kuleformel?

Totalt overflateareal av sfæren med radius r er, Areal = 4πr ²

Hva er formelen for volumet av en sfære?

Volumet av en sfære med radius r er, Volum = 4/3πr ³

Hvordan finner vi volumet på halvkulen?

Volumet av en halvkule med radius r er, Volum = 2/3πr ³

Hva er forholdet mellom volum av sfære og halvkule?

Hvis en kule og en halvkule har samme radier, er forholdet mellom volumet,

I ₁ : IN ₂ = (4/3πr ³ ): (2/3πr ³ ) = 2 : 1

Hva er volumenheten til en kule?

Volum av sfæren måles i m ³ , cm ³ , liter osv. m ³ er standard måleenhet.

Hva er volumet av sfæren når radiusen er halvert?

Volum av kule = (4/3)πr ³ = (4/3)π(r/2) ³ = (4/3)π(r ³ /8) = Volum/8. Så volumet av sfæren får en åttendedel.