Tid og rom kompleksitetsanalyse av Merge Sort
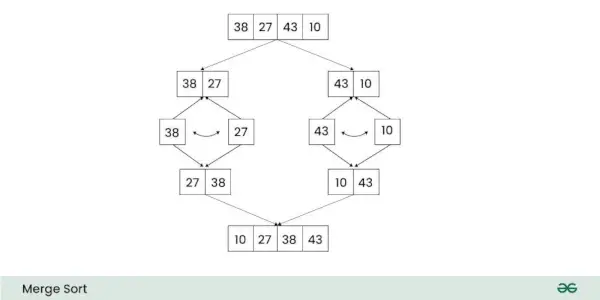
De Tidskompleksitet av Merge Sort er O(n log n) i begge gjennomsnitt og verste tilfeller . Romkompleksiteten til Slå sammen sortering er På) . 
| Aspekt | Kompleksitet |
|---|---|
| Tidskompleksitet | O(n log n) |
| Plass kompleksitet | På) |
Tidskompleksitetsanalyse av sammenslåingssortering:
Vurder følgende terminologier:
T(k) = tid det tar å sortere k elementer
M(k) = tiden det tar å slå sammen k elementer
Så det kan skrives
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + konstant * N
Disse N/2-elementene er videre delt inn i to halvdeler. Så,
T(N) = 2 * [2 * T(N/4) + konstant * N/2] + konstant * N
= 4 * T(N/4) + 2 * N * konstant
. . .
= 2 k * T(N/2 k ) + k * N * konstant
Den kan maksimalt deles inntil det er ett element igjen. Så da N/2 k = 1. k = log 2 N
T(N) = N * T(1) + N * log 2 N * konstant
= N + N * log 2 N
Derfor er tidskompleksiteten O(N * log 2 N) .
Så i beste tilfelle, verste tilfelle og gjennomsnittlig tilfelle er tidskompleksiteten den samme.
Romkompleksitetsanalyse av sammenslåingssortering:
Slå sammen sortering har en plass kompleksitet av På) . Dette er fordi den bruker en hjelpematrise av størrelse n for å slå sammen de sorterte halvdelene av inndatamatrisen. Hjelpematrisen brukes til å lagre det sammenslåtte resultatet, og inndatamatrisen overskrives med det sorterte resultatet.