Søk i binært søketre (BST)

Gitt en BST , er oppgaven å søke en node i denne BST .
For å søke etter en verdi i BST, betrakt den som en sortert matrise. Nå kan vi enkelt utføre søkeoperasjon i BST ved hjelp av Binær søkealgoritme .
Algoritme for å søke etter en nøkkel i et gitt binært søketre:
La oss si at vi vil søke etter nummeret X, Vi starter ved roten. Deretter:
- Vi sammenligner verdien som skal søkes med verdien til roten.
- Hvis det er likt, er vi ferdige med søket hvis det er mindre, vi vet at vi må gå til venstre undertre fordi i et binært søketre er alle elementene i venstre undertre mindre og alle elementene i høyre undertre er større.
- Gjenta trinnet ovenfor til det ikke er mulig å krysse mer
- Hvis nøkkelen blir funnet ved en iterasjon, returner True. Ellers Falsk.
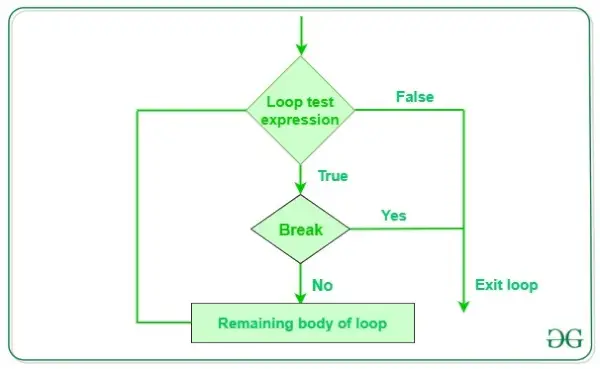
Illustrasjon av søk i en BST:
Se illustrasjonen nedenfor for en bedre forståelse:
Anbefalt fremgangsmåteSøk i en node i BSTTry It!

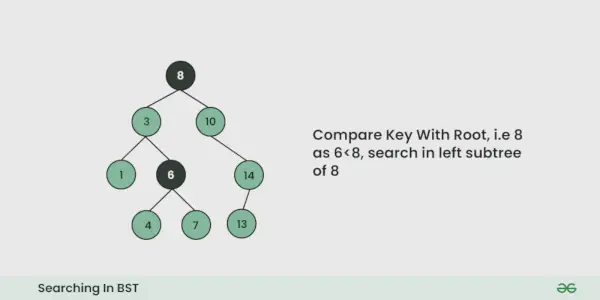
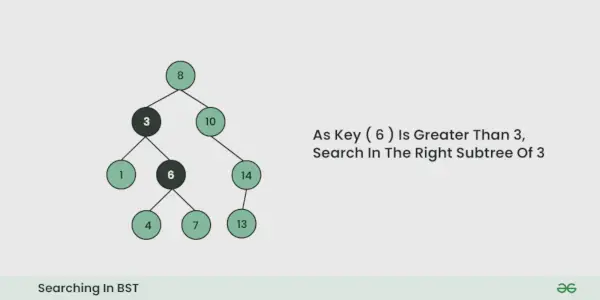
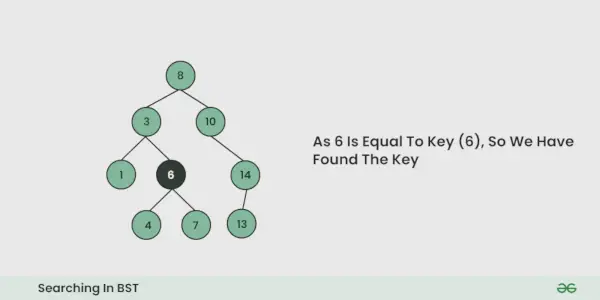
Program for å implementere søk i BST:
C++
// C++ function to search a given key in a given BST> #include> using> namespace> std;> struct> node {> > int> key;> > struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(> int> item)> {> > struct> node* temp> > => new> struct> node;> > temp->nøkkel = element;> > temp->venstre = temp->høyre = NULL;> > return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(> struct> node* node,> int> key)> {> > // If the tree is empty, return a new node> > if> (node == NULL)> > return> newNode(key);> > // Otherwise, recur down the tree> > if> (key key)> > node->venstre = insert(node->venstre, tast);> > else> if> (key>node->nøkkel)> > node->høyre = insert(node->høyre, nøkkel);> > // Return the (unchanged) node pointer> > return> node;> }> // Utility function to search a key in a BST> struct> node* search(> struct> node* root,> int> key)> > > // Base Cases: root is null or key is present at root> > if> (root == NULL> // Driver Code> int> main()> {> > struct> node* root = NULL;> > root = insert(root, 50);> > insert(root, 30);> > insert(root, 20);> > insert(root, 40);> > insert(root, 70);> > insert(root, 60);> > insert(root, 80);> > // Key to be found> > int> key = 6;> > // Searching in a BST> > if> (search(root, key) == NULL)> > cout < < key < <> ' not found'> < < endl;> > else> > cout < < key < <> ' found'> < < endl;> > key = 60;> > // Searching in a BST> > if> (search(root, key) == NULL)> > cout < < key < <> ' not found'> < < endl;> > else> > cout < < key < <> ' found'> < < endl;> > return> 0;> }> |
C
// C function to search a given key in a given BST> #include> #include> struct> node {> > int> key;> > struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(> int> item)> {> > struct> node* temp> > = (> struct> node*)> malloc> (> sizeof> (> struct> node));> > temp->nøkkel = element;> > temp->venstre = temp->høyre = NULL;> > return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(> struct> node* node,> int> key)> {> > // If the tree is empty, return a new node> > if> (node == NULL)> > return> newNode(key);> > // Otherwise, recur down the tree> > if> (key key)> > node->venstre = insert(node->venstre, tast);> > else> if> (key>node->nøkkel)> > node->høyre = insert(node->høyre, nøkkel);> > // Return the (unchanged) node pointer> > return> node;> }> // Utility function to search a key in a BST> struct> node* search(> struct> node* root,> int> key)> > // Driver Code> int> main()> {> > struct> node* root = NULL;> > root = insert(root, 50);> > insert(root, 30);> > insert(root, 20);> > insert(root, 40);> > insert(root, 70);> > insert(root, 60);> > insert(root, 80);> > // Key to be found> > int> key = 6;> > // Searching in a BST> > if> (search(root, key) == NULL)> > printf> (> '%d not found
'> , key);> > else> > printf> (> '%d found
'> , key);> > key = 60;> > // Searching in a BST> > if> (search(root, key) == NULL)> > printf> (> '%d not found
'> , key);> > else> > printf> (> '%d found
'> , key);> > return> 0;> }> |
Java
// Java program to search a given key in a given BST> class> Node {> > int> key;> > Node left, right;> > public> Node(> int> item) {> > key = item;> > left = right => null> ;> > }> }> class> BinarySearchTree {> > Node root;> > // Constructor> > BinarySearchTree() {> > root => null> ;> > }> > // A utility function to insert> > // a new node with given key in BST> > Node insert(Node node,> int> key) {> > // If the tree is empty, return a new node> > if> (node ==> null> ) {> > node => new> Node(key);> > return> node;> > }> > // Otherwise, recur down the tree> > if> (key node.left = insert(node.left, key); else if (key>node.key) node.right = insert(node.right, key); // Returner (uendret) nodepeker returnode; } // Utility-funksjon for å søke etter en nøkkel i et BST Node-søk(Node-rot, int-nøkkel) // Driver Code public static void main(String[] args) { BinarySearchTree tree = new BinarySearchTree(); // Setter inn noder tree.root = tree.insert(tree.root, 50); tree.insert(tre.root, 30); tree.insert(tre.root, 20); tree.insert(tre.root, 40); tree.insert(tre.root, 70); tree.insert(tre.root, 60); tree.insert(tre.root, 80); // Nøkkel som skal finnes int nøkkel = 6; // Søker i en BST if (tree.search(tree.root, key) == null) System.out.println(key + ' ikke funnet'); else System.out.println(nøkkel + ' funnet'); nøkkel = 60; // Søker i en BST if (tree.search(tree.root, key) == null) System.out.println(key + ' ikke funnet'); else System.out.println(tast + ' funnet'); } }> |
Python3
# Python3 function to search a given key in a given BST> class> Node:> > # Constructor to create a new node> > def> __init__(> self> , key):> > self> .key> => key> > self> .left> => None> > self> .right> => None> # A utility function to insert> # a new node with the given key in BST> def> insert(node, key):> > # If the tree is empty, return a new node> > if> node> is> None> :> > return> Node(key)> > # Otherwise, recur down the tree> > if> key node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Returner (uendret) nodepeker returnode # Utility-funksjon for å søke etter en nøkkel i et BST def search(root, key): # Grunntilfeller: root er null eller nøkkel er tilstede ved root hvis root er Ingen eller root.key == nøkkel: returner rot # Nøkkel er større enn roots nøkkel hvis root.key returner søk(root.right, key) # Nøkkel er mindre enn root 's key return search(root.left, key) # Driver Code if __name__ == '__main__': root = Ingen rot = insert(root, 50) insert(root, 30) insert(root, 20) insert (root, 40) insert(root, 70) insert(root, 60) insert(root, 80) # Key to be found key = 6 # Søker i en BST hvis søk(root, key) er Ingen: print(key, 'not found') else: print(key, 'found') key = 60 # Søker i en BST hvis søk(root, key) er Ingen: print(key, 'not found') else: print(nøkkel, 'funnet')> |
C#
// C# function to search a given key in a given BST> using> System;> public> class> Node {> > public> int> key;> > public> Node left, right;> }> public> class> BinaryTree {> > // A utility function to create a new BST node> > public> Node NewNode(> int> item)> > {> > Node temp => new> Node();> > temp.key = item;> > temp.left = temp.right => null> ;> > return> temp;> > }> > // A utility function to insert> > // a new node with given key in BST> > public> Node Insert(Node node,> int> key)> > {> > // If the tree is empty, return a new node> > if> (node ==> null> )> > return> NewNode(key);> > // Otherwise, recur down the tree> > if> (key node.left = Insert(node.left, key); else if (key>node.key) node.right = Sett inn(node.høyre, nøkkel); // Returner (uendret) nodepeker returnode; } // Utility-funksjon for å søke etter en nøkkel i en BST offentlig nodesøk(Noderot, int-nøkkel) // Grunntilfeller: root er null eller nøkkel er tilstede ved root if (root == null // Driverkode offentlig statisk void Main () { Node root = null BinaryTree bt = new BinaryTree(); , 40); bt.Insert(root, 70); bt.Search(root, key) == null) Console.WriteLine(key + 'ikke funnet'); if (bt.Search(root, key) == null) Console.WriteLine(nøkkel + ' ikke funnet'); |
>
// Javascript function to search a given key in a given BST>class Node {>>constructor(key) {>>this>.key = key;>>this>.left =>null>;>>this>.right =>null>;>>}>}>// A utility function to insert>// a new node with given key in BST>function>insert(node, key) {>>// If the tree is empty, return a new node>>if>(node ===>null>) {>>return>new>Node(key);>>}>>// Otherwise, recur down the tree>>if>(key node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Returner den (uendrede) nodepekeren returnoden; } // Utility-funksjon for å søke etter en nøkkel i et BST-funksjonssøk(root, key) { // Grunntilfeller: root er null eller nøkkel er til stede ved root if (root === null || root.key === nøkkel ) { returner rot; } // Nøkkelen er større enn rotnøkkelen if (root.key return search(root.right, key); } // Nøkkelen er mindre enn rotens nøkkel retursøk(root.left, key); } // Driver Code la root = insert(root, 30 insert(root, 70); 60); insert(root, 80); // Key to be found let key = 6; // Søker i en BST if (søk(root, key) === null) funnet'); } else { console.log(key + ' found' } key = 60; tast + ' ikke funnet'); } else { console.log(tast + ' funnet' }>
Produksjon
6 not found 60 foundTidskompleksitet: O(h), hvor h er høyden til BST.
Hjelpeplass: O(h), hvor h er høyden til BST. Dette er fordi den maksimale mengden plass som trengs for å lagre rekursjonsstakken vil være h .Relaterte linker:
- Binær søketre-innsettingsoperasjon
- Sletting av binært søketre