Forutsetning: Lineær regresjon

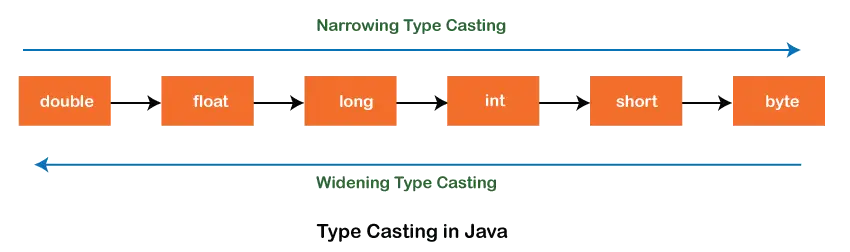
Lineær regresjon er en maskinlæringsalgoritme basert på overvåket læring. Den utfører en regresjonsoppgave. Regresjon modellerer en målprediksjonsverdi basert på uavhengige variabler. Det brukes mest for å finne ut forholdet mellom variabler og prognoser. Ulike regresjonsmodeller er forskjellige basert på – hva slags forhold mellom de avhengige og uavhengige variablene de vurderer og antall uavhengige variabler som brukes. Denne artikkelen skal demonstrere hvordan du bruker de forskjellige Python-bibliotekene til å implementere lineær regresjon på et gitt datasett. Vi vil demonstrere en binær lineær modell da denne vil være lettere å visualisere. I denne demonstrasjonen vil modellen bruke Gradient Descent for å lære. Du kan lære om det her.

Trinn 1: Importerer alle nødvendige biblioteker

Python3

import> numpy as np> import> pandas as pd> import> seaborn as sns> import> matplotlib.pyplot as plt> from> sklearn> import> preprocessing, svm> from> sklearn.model_selection> import> train_test_split> from> sklearn.linear_model> import> LinearRegression>

Steg 2: Leser datasettet:

Python3

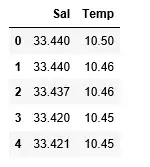
df> => pd.read_csv(> 'bottle.csv'> )> df_binary> => df[[> 'Salnty'> ,> 'T_degC'> ]]> > # Taking only the selected two attributes from the dataset> df_binary.columns> => [> 'Sal'> ,> 'Temp'> ]> #display the first 5 rows> df_binary.head()>

Produksjon:

Trinn 3: Utforsker dataspredningen

Python3

#plotting the Scatter plot to check relationship between Sal and Temp> sns.lmplot(x> => 'Sal'> , y> => 'Temp'> , data> => df_binary, order> => 2> , ci> => None> )> plt.show()>

Produksjon:

Trinn 4: Datarensing

Python3

# Eliminating NaN or missing input numbers> df_binary.fillna(method> => 'ffill'> , inplace> => True> )>

Trinn 5: Trening av modellen vår

Python3

X> => np.array(df_binary[> 'Sal'> ]).reshape(> -> 1> ,> 1> )> y> => np.array(df_binary[> 'Temp'> ]).reshape(> -> 1> ,> 1> )> > # Separating the data into independent and dependent variables> # Converting each dataframe into a numpy array> # since each dataframe contains only one column> df_binary.dropna(inplace> => True> )> > # Dropping any rows with Nan values> X_train, X_test, y_train, y_test> => train_test_split(X, y, test_size> => 0.25> )> > # Splitting the data into training and testing data> regr> => LinearRegression()> > regr.fit(X_train, y_train)> print> (regr.score(X_test, y_test))>

Produksjon:

Trinn 6: Utforsker resultatene våre

Python3

y_pred> => regr.predict(X_test)> plt.scatter(X_test, y_test, color> => 'b'> )> plt.plot(X_test, y_pred, color> => 'k'> )> > plt.show()> # Data scatter of predicted values>

Produksjon:

Den lave nøyaktighetsskåren til modellen vår antyder at vår regressive modell ikke passer særlig godt med eksisterende data. Dette antyder at våre data ikke er egnet for lineær regresjon. Men noen ganger kan et datasett godta en lineær regressor hvis vi bare vurderer en del av den. La oss se etter den muligheten.

Trinn 7: Arbeid med et mindre datasett

Python3

df_binary500> => df_binary[:][:> 500> ]> > # Selecting the 1st 500 rows of the data> sns.lmplot(x> => 'Sal'> , y> => 'Temp'> , data> => df_binary500,> > order> => 2> , ci> => None> )>

Produksjon:

Vi kan allerede se at de første 500 radene følger en lineær modell. Fortsetter med de samme trinnene som før.

Python3

df_binary500.fillna(method> => 'fill'> , inplace> => True> )> > X> => np.array(df_binary500[> 'Sal'> ]).reshape(> -> 1> ,> 1> )> y> => np.array(df_binary500[> 'Temp'> ]).reshape(> -> 1> ,> 1> )> > df_binary500.dropna(inplace> => True> )> X_train, X_test, y_train, y_test> => train_test_split(X, y, test_size> => 0.25> )> > regr> => LinearRegression()> regr.fit(X_train, y_train)> print> (regr.score(X_test, y_test))>

Produksjon:

Python3

y_pred> => regr.predict(X_test)> plt.scatter(X_test, y_test, color> => 'b'> )> plt.plot(X_test, y_pred, color> => 'k'> )> > plt.show()>

Produksjon:

Trinn 8: Evalueringsberegninger for regresjon

Til slutt sjekker vi ytelsen til den lineære regresjonsmodellen ved hjelp av evalueringsmålinger. For regresjonsalgoritmer bruker vi mye mean_absolute_error og mean_squared_error-beregninger for å sjekke modellens ytelse.

Python3

from> sklearn.metrics> import> mean_absolute_error,mean_squared_error> > mae> => mean_absolute_error(y_true> => y_test,y_pred> => y_pred)> #squared True returns MSE value, False returns RMSE value.> mse> => mean_squared_error(y_true> => y_test,y_pred> => y_pred)> #default=True> rmse> => mean_squared_error(y_true> => y_test,y_pred> => y_pred,squared> => False> )> > print> (> 'MAE:'> ,mae)> print> (> 'MSE:'> ,mse)> print> (> 'RMSE:'> ,rmse)>

Produksjon:

MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078