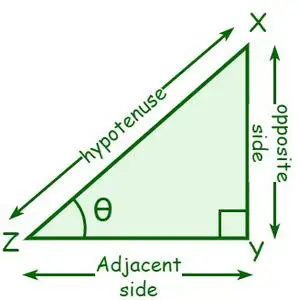
Vinkel mellom to vektorer formel

Vinkel mellom to vektorer er vinkelen mellom halene deres, og denne vinkelen kan enkelt finnes ved å bruke kryssprodukt og punktprodukt av vektorformler. Vinkelen mellom to vektorer ligger alltid mellom 0° og 180°.
I denne artikkelen vil vi lære om, vinkel mellom to vektorer, definisjon, formler og eksempler i detalj.
Hva er vinkelen mellom to vektorer?
Vinkel mellom to vektorer er vinkelen som dannes ved skjæringspunktet mellom halene deres. Vinkelen mellom to vektorer kan være spiss, rett eller stump, avhengig av retningen til vektorene.
Vinkel mellom to vektorer er funnet ved å bruke to formler:
- Bruke punktprodukt av vektorer
- Bruke kryssprodukt av vektorer
Dette er forklart i formelen nedenfor.
Vinkel mellom to vektorformler
Vinkel mellom to vektorer er lett og oftest funnet ved å bruke skalarprodukt av vektorer.

To vektorer A og B
Prikk produkt av A og B er gitt av,
vec{A}.vec{B} = |A| |B| cosθ.
Spesielle tilfeller
- Når vinkelen mellom vektorer er 0 grader.
Det vil si θ = 0°
⇒ |A| |B| cosθ
⇒ |A| |B| cos0°
⇒ |A| |B| [cos0° = 1]
- Når vinkelen mellom vektorer er 180 grader.
⇒ |A| |B| cosθ
⇒ |A| |B| cos180°
⇒ – |A| |B| [cos180° = -1]
- Når vinkelen mellom vektorer er 90 grader.
⇒ |A| |B| cosθ
⇒ |A| |B| cos90°
⇒ |A| |B| × 0 [cos90° = 0]
⇒ 0
Formel for vinkel mellom to vektorer
Cosinus av vinkelen mellom to vektorer er lik summen av produktet av de individuelle komponentene i de to vektorene, delt på produktet av størrelsen til de to vektorene.
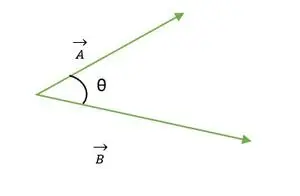
To vektorer A og B
cosθ=
θ= cos -1
I kartesisk form,
A = A x i + A og j + A Med k
B= B x i + B og j + B Med k
cos θ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}
Egenskaper til Dot-produktet
- Punktprodukt er kommutativt
vec{A}.vec{B}=vec{B}.vec{A}
- Dot-produktet er distribuerende
vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})
Vinkelen mellom to vektorer ligger mellom 0 ≤ θ ≤ 180. Når halene eller hodene til begge vektorene faller sammen, beregnes vinkelen mellom vektorene.
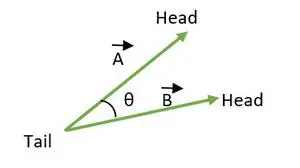
Halen sammenfaller
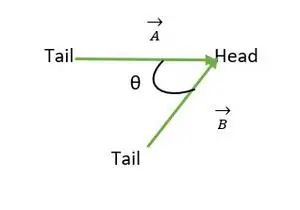
Hodet sammenfaller
Eksempel på problemer Vinkel mellom to vektorer Formel
Oppgave 1: Finn vinkelen mellom vektorer (hvis de danner en likesidet trekant)
- a og b vektorer
- b og c vektorer
- a og c vektorer
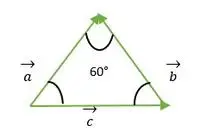
Likesidet trekant dannet av a, b, c vektor
Løsning:
- a og b vektorer
For vektor a og b faller hodet til begge vektorene med hverandre, og vinkelen mellom a og b vektor er derfor den samme som vinkelen mellom to sider av likesidet trekant = 60°.
- b og c vektorer:
Fra figuren ovenfor ser vi at hodet eller halen til b- og c-vektoren ikke sammenfaller med hverandre.
Så, ved å bruke egenskapen- En vektor forblir uendret hvis den overføres parallelt med seg selv.
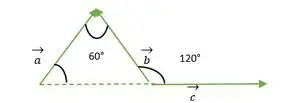
Vektor c forskyves parallelt med seg selv
Nå ser vi halen til vektorene b og c er sammenfallende med hverandre, derfor er den samme som den ytre vinkelen gjør med en likesidet trekant = 120°.
- a og c vektorer

Halen til a og c faller sammen
For vektorene a og c faller halen til begge vektorene sammen med hverandre, derfor er vinkelen mellom a- og c-vektoren den samme som vinkelen mellom to sider av den likesidede trekanten = 60°.
Oppgave 2: Finn vinkler mellom vektorer hvis de danner en likebenet rettvinklet trekant.
- a og b vektor
- b og c vektor
- a og c vektorer
Løsning:
- a og b vektor

Rett vinkel Likebenet trekant
Fra figuren ovenfor ser vi at hodet eller halen til a- og b-vektoren ikke sammenfaller med hverandre. Så, ved å bruke egenskapen- En vektor forblir uendret hvis den overføres parallelt med seg selv.
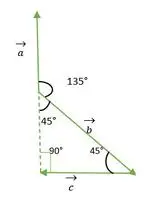
en vektor forskyves parallelt med seg selv
Nå faller a og b vektorhaler sammen med hverandre og danner en vinkel som er den samme som den ytre vinkelen til en rettvinklet likebenet trekant = 135°.
- b og c vektor

Rett vinkel Likebenet trekant
Fra figuren ovenfor faller ikke b og c vektorhode eller haler sammen med hverandre. Så, ved å bruke egenskapen, forblir en vektor uendret hvis den overføres parallelt med seg selv.
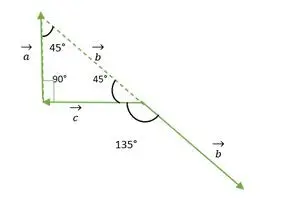
b vektor forskyves parallelt med seg selv
Nå faller b- og c-vektorens haler sammen og danner en vinkel som er den samme som den ytre vinkelen til en rettvinklet likebenet trekant = 135°.
- a og c vektorer

Rett vinkel Likebenet trekant
Fra figuren ovenfor faller ikke a og c vektorhode eller haler sammen med hverandre. Så, ved å bruke egenskapen- En vektor forblir uendret hvis den overføres parallelt med seg selv.
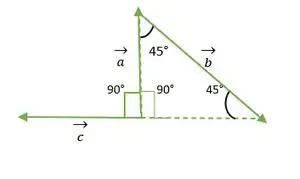
c vektor flyttes parallelt med seg selv
Nå faller a og c vektorhaler sammen med hverandre og danner en vinkel som er den samme som den rette vinkelen til likebenet trekant = 90°.
Oppgave 3: Finn vinkel mellom vektorene A = i + j + k og vektor B = -2i – 2j – 2k.
Løsning:
Fra formelen,
A = A x i + A og j + A Med k
B= B x i + B og j + B Med k
cosθ=
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Her i det gitte spørsmålet,
A= i + j + k
B= -2i -2j -2k
Erstatter verdiene i formelen
⇒ cosθ =
frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})} ⇒ cosθ =
frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})} ⇒ cosθ =
frac{-6}{(sqrt{3}×sqrt{12})} ⇒ cosθ =
frac{-6}{(sqrt{36})} ⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°
Oppgave 4: Finn vinkelen mellom vektor A = 3i + 4j og B = 2i + j
Løsning:
A = A x i + A og j + A Med k
B = B x i + B og j + B Med k
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Her gitt,
A= 3i + 4j + 0k
B= 2i + j + 0k
erstatte verdiene i formelen,
⇒ cosθ =
frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})} ⇒ cosθ =
frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})} ⇒ cosθ =
frac{(10)}{(sqrt{25}×sqrt{5})} ⇒ cosθ =
frac{(10)}{(sqrt{125})} ⇒ θ = cos -1 (
frac{(10)}{5.(sqrt{5})} )⇒ θ = cos -1 (
frac{2}{(sqrt{5})} )
Oppgave 5: Finn vinkelen mellom vektor A = i + j og vektor B = j + k.
Løsning:
Fra formelen,
A = A x i + A og j + A Med k
B = B x i + B og j + B Med k
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Her i det gitte spørsmålet,
⇒ A = i + j
⇒ B = j + k
⇒ cosθ =
frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})} ⇒ cosθ =
frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})} ⇒ cosθ =
frac{1}{(sqrt{2}×sqrt{2})} ⇒ θ = cos -1 (1/2)
⇒ θ = 60°