Druk alle manieren af om een tekenreeks in bracket -vorm te breken
Gegeven een tekenreeks vind alle manieren om de gegeven string in bracket -vorm te breken. Voeg elke substring binnen een haakjes in.
Voorbeelden:
Input : abc Output: (a)(b)(c) (a)(bc) (ab)(c) (abc) Input : abcd Output : (a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
We raden u ten zeerste aan om uw browser te minimaliseren en dit eerst zelf te proberen.
Het idee is om recursie te gebruiken. We handhaven twee parameters - index van het volgende te verwerken teken en de uitvoerreeks tot nu toe. We starten van de index van het volgende teken dat moet worden verwerkt, appen -substring gevormd door onbewerkte string naar de uitvoerreeks en herstellen bij de resterende string totdat we de hele string verwerken. We gebruiken std :: substr om de uitvoerreeks te vormen. Substr (pos n) retourneert een substring van lengte n die begint bij positie POS van de huidige string.
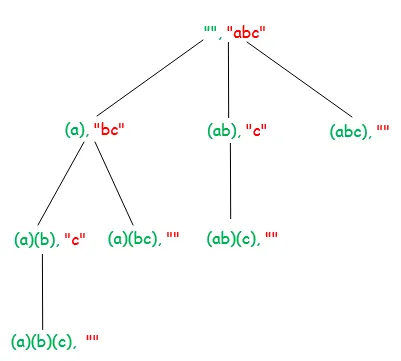
Onder het diagram toont de recursieboom voor invoerreeks 'ABC'. Elk knooppunt op het diagram toont verwerkte string (gemarkeerd door groen) en onbewerkte string (gemarkeerd door rood).

Hieronder is de implementatie van het bovenstaande idee
C++ // C++ Program to find all combinations of Non- // overlapping substrings formed from given // string #include using namespace std ; // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far void findCombinations ( string str int index string out ) { if ( index == str . length ()) cout < < out < < endl ; for ( int i = index ; i < str . length (); i ++ ) { // append substring formed by str[index // i] to output string findCombinations ( str i + 1 out + '(' + str . substr ( index i + 1 - index ) + ')' ); } } // Driver Code int main () { // input string string str = 'abcd' ; findCombinations ( str 0 '' ); return 0 ; }
Java // Java program to find all combinations of Non- // overlapping substrings formed from given // string class GFG { // find all combinations of non-overlapping // substrings formed by input string str static void findCombinations ( String str int index String out ) { if ( index == str . length ()) System . out . println ( out ); for ( int i = index ; i < str . length (); i ++ ) // append substring formed by str[index // i] to output string findCombinations ( str i + 1 out + '(' + str . substring ( index i + 1 ) + ')' ); } // Driver Code public static void main ( String [] args ) { // input string String str = 'abcd' ; findCombinations ( str 0 '' ); } } // Contributed by Pramod Kumar
Python3 # Python3 Program to find all combinations of Non- # overlapping substrings formed from given # string # find all combinations of non-overlapping # substrings formed by input string str # index – index of the next character to # be processed # out - output string so far def findCombinations ( string index out ): if index == len ( string ): print ( out ) for i in range ( index len ( string ) 1 ): # append substring formed by str[index # i] to output string findCombinations ( string i + 1 out + '(' + string [ index : i + 1 ] + ')' ) # Driver Code if __name__ == '__main__' : # input string string = 'abcd' findCombinations ( string 0 '' ) # This code is contributed by # sanjeev2552
C# // C# program to find all combinations // of Non-overlapping substrings formed // from given string using System ; class GFG { // find all combinations of non-overlapping // substrings formed by input string str public static void findCombinations ( string str int index string @out ) { if ( index == str . Length ) { Console . WriteLine ( @out ); } for ( int i = index ; i < str . Length ; i ++ ) { // append substring formed by // str[index i] to output string findCombinations ( str i + 1 @out + '(' + str . Substring ( index ( i + 1 ) - index ) + ')' ); } } // Driver Code public static void Main ( string [] args ) { // input string string str = 'abcd' ; findCombinations ( str 0 '' ); } } // This code is contributed by Shrikant13
JavaScript // Javascript program for the above approach // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far function findCombinations ( string index out ) { if ( index == string . length ) { console . log ( out ); } for ( let i = index ; i < string . length ; i ++ ) { // append substring formed by str[index // i] to output string findCombinations ( string i + 1 out + '(' + string . substring ( index i + 1 ) + ')' ); } } // Driver Code const string = 'abcd' ; findCombinations ( string 0 '' ); // contributed by adityasharmadev01
Uitvoer
(a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Tijdcomplexiteit: O (n 2 ))
Hulpruimte: O (n 2 ))