Maximaal element tussen twee knooppunten van BST
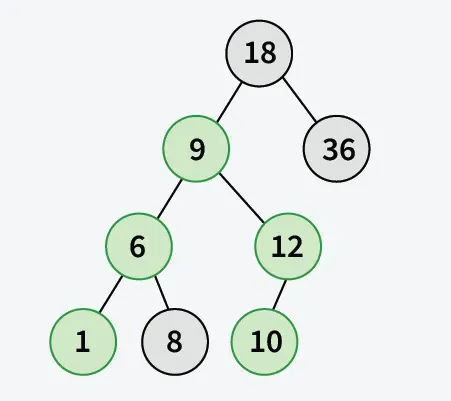
Gegeven een array van N elementen en twee gehele getallen een b die tot de gegeven array behoren. Maak een Binaire zoekboom door elementen in te voegen uit arr[0] tot arr[n-1] . De taak is om de maximaal element in het pad van a naar b.
Voorbeeld:
Invoer: arr[] = { 18 36 9 6 12 10 1 8 } a = 1 b = 10.
Uitgang: 12
Uitleg: Pad van 1 tot 10 bevat { 1 6 9 12 10 } . Het maximale element is 12.
Inhoudsopgave
- [Naïeve aanpak] Hashen gebruiken - O(n * log n) Tijd en O(n) Ruimte
- [Verwachte aanpak] Met behulp van LCA van twee knooppunten: O(h) Tijd en O(h) Ruimte
[Naïeve aanpak] Hashen gebruiken - O(n * log n) Tijd en O(n) Ruimte
Het idee is om gebruik te maken van een hashmap om de op te slaan ouder knooppunt van elk knooppunt in de binaire zoekboom . We kunnen beginnen bij beide gegeven knooppunten en de boom doorkruisen, waarbij we de knooppunten opslaan die we tegenkomen in a set . Zodra we de wortel of een gemeenschappelijke voorouder van de twee knooppunten hebben bereikt, kunnen we vanaf elk knooppunt de boom doorkruisen en de maximaal element dat voorkomt in de reeks knooppunten.
Algoritmestappen voor de bovenstaande aanpak:
- Maak een leeg hash-tabel om de op te slaan ouder knooppunt van elk knooppunt in de binaire zoekboom.
- Voer een uit diepte-eerst zoeken (DFS) doorloop de binaire zoekboom en vul de hashtabel met het bovenliggende knooppunt van elk knooppunt.
- Initialiseer twee wijzers, zeg p1 en p2 naar de gegeven knooppunten.
- Initialiseer bijvoorbeeld twee lege sets s1 en s2 om de knooppunten op te slaan die u tegenkomt tijdens het doorkruisen van de boom p1 en p2 respectievelijk.
- Terwijl p1 en p2 Zijn niet gelijk doe het volgende:
- Als p1 dat niet is nul voeg het toe aan set s1 en update p1 naar het bovenliggende knooppunt met behulp van de hashtabel.
- Als p2 dat niet is nul voeg het toe aan set s2 en update p2 naar het bovenliggende knooppunt met behulp van de hashtabel.
- Zoek de snijpuntset van s1 en s2 dat wil zeggen de reeks knooppunten die gemeenschappelijk zijn voor zowel s1 als s2.
- Op dit kruispunt vind je maximaal element en retourneer het.
Hieronder vindt u de implementatie van de bovenstaande aanpak:
C++ // C++ program to find maximum element in the path // between two Nodes of Binary Search Tree. #include using namespace std ; class Node { public : int data ; Node * left * right ; Node ( int x ) { data = x ; left = right = nullptr ; } }; // Insert a new Node in Binary Search Tree void insertNode ( Node *& root int x ) { Node * current = root * parent = nullptr ; // Traverse to the correct position for insertion while ( current != nullptr ) { parent = current ; if ( x < current -> data ) current = current -> left ; else current = current -> right ; } // Insert new Node at the correct position if ( parent == nullptr ) root = new Node ( x ); else if ( x < parent -> data ) parent -> left = new Node ( x ); else parent -> right = new Node ( x ); } // DFS to populate parent map for each node void dfs ( Node * root unordered_map < Node * Node *> & parentMap Node * parent = nullptr ) { if ( ! root ) return ; // Store the parent of the current node if ( parent != nullptr ) { parentMap [ root ] = parent ; } // Recur for left and right children dfs ( root -> left parentMap root ); dfs ( root -> right parentMap root ); } // Function to find the node with the given value in the BST Node * findNode ( Node * root int val ) { if ( ! root ) return nullptr ; if ( root -> data == val ) return root ; Node * leftResult = findNode ( root -> left val ); if ( leftResult ) return leftResult ; return findNode ( root -> right val ); } // Find maximum element in the path between two nodes in BST int findMaxElement ( Node * root int x int y ) { unordered_map < Node * Node *> parentMap ; // Populate parent map with DFS dfs ( root parentMap ); // Find the nodes corresponding to the // values x and y Node * p1 = findNode ( root x ); Node * p2 = findNode ( root y ); // If nodes not found if ( ! p1 || ! p2 ) return -1 ; // Sets to store nodes encountered // while traversing up the tree unordered_set < Node *> s1 s2 ; // Variable to store the maximum // element in the path int maxElement = INT_MIN ; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while ( p1 != p2 ) { if ( p1 ) { s1 . insert ( p1 ); maxElement = max ( maxElement p1 -> data ); // Move to parent node p1 = parentMap [ p1 ]; } if ( p2 ) { s2 . insert ( p2 ); maxElement = max ( maxElement p2 -> data ); p2 = parentMap [ p2 ]; } // Check if there's a common node // in both sets if ( s1 . count ( p2 )) break ; if ( s2 . count ( p1 )) break ; } // Now both p1 and p2 point to their Lowest // Common Ancestor (LCA) maxElement = max ( maxElement p1 -> data ); return maxElement ; } int main () { vector < int > arr = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; int n = arr . size (); Node * root = new Node ( arr [ 0 ]); for ( int i = 1 ; i < n ; i ++ ) insertNode ( root arr [ i ]); cout < < findMaxElement ( root a b ) < < endl ; return 0 ; }
Java // Java program to find the maximum element in the path // between two Nodes of Binary Search Tree. import java.util.* ; class Node { int data ; Node left right ; Node ( int x ) { data = x ; left = right = null ; } } class GfG { // Insert a new Node in Binary Search Tree static void insertNode ( Node root int x ) { Node current = root parent = null ; // Traverse to the correct position // for insertion while ( current != null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct position if ( parent == null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // DFS to populate parent map for each node static void dfs ( Node root Map < Node Node > parentMap Node parent ) { if ( root == null ) return ; // Store the parent of the current node if ( parent != null ) { parentMap . put ( root parent ); } // Recur for left and right children dfs ( root . left parentMap root ); dfs ( root . right parentMap root ); } // Function to find the node with the given // value in the BST static Node findNode ( Node root int val ) { if ( root == null ) return null ; if ( root . data == val ) return root ; Node leftResult = findNode ( root . left val ); if ( leftResult != null ) return leftResult ; return findNode ( root . right val ); } // Find maximum element in the path between // two nodes in BST static int findMaxElement ( Node root int x int y ) { Map < Node Node > parentMap = new HashMap <> (); // Populate parent map with DFS dfs ( root parentMap null ); // Find the nodes corresponding to // the values x and y Node p1 = findNode ( root x ); Node p2 = findNode ( root y ); // If nodes not found if ( p1 == null || p2 == null ) return - 1 ; // Sets to store nodes encountered // while traversing up the tree Set < Node > s1 = new HashSet <> (); Set < Node > s2 = new HashSet <> (); // Variable to store the maximum element // in the path int maxElement = Integer . MIN_VALUE ; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while ( p1 != p2 ) { if ( p1 != null ) { s1 . add ( p1 ); maxElement = Math . max ( maxElement p1 . data ); // Move to parent node p1 = parentMap . get ( p1 ); } if ( p2 != null ) { s2 . add ( p2 ); maxElement = Math . max ( maxElement p2 . data ); p2 = parentMap . get ( p2 ); } // Check if there's a common node in both sets if ( s1 . contains ( p2 )) break ; if ( s2 . contains ( p1 )) break ; } // Now both p1 and p2 point to their // Lowest Common Ancestor (LCA) maxElement = Math . max ( maxElement p1 . data ); return maxElement ; } public static void main ( String [] args ) { int [] arr = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; int n = arr . length ; Node root = new Node ( arr [ 0 ] ); for ( int i = 1 ; i < n ; i ++ ) insertNode ( root arr [ i ] ); System . out . println ( findMaxElement ( root a b )); } }
Python # Python program to find maximum element in the path # between two Nodes of Binary Search Tree. class Node : def __init__ ( self x ): self . data = x self . left = None self . right = None # Insert a new Node in Binary Search Tree def insert_node ( root x ): current = root parent = None # Traverse to the correct position for insertion while current is not None : parent = current if x < current . data : current = current . left else : current = current . right # Insert new Node at the correct position if parent is None : root = Node ( x ) elif x < parent . data : parent . left = Node ( x ) else : parent . right = Node ( x ) # DFS to populate parent map for each node def dfs ( root parent_map parent = None ): if root is None : return # Store the parent of the current node if parent is not None : parent_map [ root ] = parent # Recur for left and right children dfs ( root . left parent_map root ) dfs ( root . right parent_map root ) # Function to find the node with the given # value in the BST def find_node ( root val ): if root is None : return None if root . data == val : return root left_result = find_node ( root . left val ) if left_result : return left_result return find_node ( root . right val ) # Find maximum element in the path between # two nodes in BST def find_max_element ( root x y ): parent_map = {} # Populate parent map with DFS dfs ( root parent_map ) # Find the nodes corresponding to the # values x and y p1 = find_node ( root x ) p2 = find_node ( root y ) # If nodes not found if not p1 or not p2 : return - 1 # Sets to store nodes encountered # while traversing up the tree s1 = set () s2 = set () # Variable to store the maximum element in the path max_element = float ( '-inf' ) # Traverse up the tree from p1 and p2 # and add nodes to sets s1 and s2 while p1 != p2 : if p1 : s1 . add ( p1 ) max_element = max ( max_element p1 . data ) # Move to parent node p1 = parent_map . get ( p1 ) if p2 : s2 . add ( p2 ) max_element = max ( max_element p2 . data ) p2 = parent_map . get ( p2 ) # Check if there's a common node in both sets if p2 in s1 : break if p1 in s2 : break # Now both p1 and p2 point to their # Lowest Common Ancestor (LCA) max_element = max ( max_element p1 . data ) return max_element if __name__ == '__main__' : arr = [ 18 36 9 6 12 10 1 8 ] a b = 1 10 n = len ( arr ) root = Node ( arr [ 0 ]) for i in range ( 1 n ): insert_node ( root arr [ i ]) print ( find_max_element ( root a b ))
C# // C# program to find the maximum element in the path // between two Nodes of Binary Search Tree. using System ; using System.Collections.Generic ; class Node { public int data ; public Node left right ; public Node ( int x ) { data = x ; left = right = null ; } } class GfG { // Insert a new Node in Binary Search Tree static public void insertNode ( Node root int x ) { Node current = root parent = null ; // Traverse to the correct position // for insertion while ( current != null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct // position if ( parent == null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // DFS to populate parent map for each node static public void dfs ( Node root Dictionary < Node Node > parentMap Node parent ) { if ( root == null ) return ; // Store the parent of the current node if ( parent != null ) { parentMap [ root ] = parent ; } // Recur for left and right children dfs ( root . left parentMap root ); dfs ( root . right parentMap root ); } // Function to find the node with the given // value in the BST static public Node findNode ( Node root int val ) { if ( root == null ) return null ; if ( root . data == val ) return root ; Node leftResult = findNode ( root . left val ); if ( leftResult != null ) return leftResult ; return findNode ( root . right val ); } // Find maximum element in the path between // two nodes in BST static public int findMaxElement ( Node root int x int y ) { Dictionary < Node Node > parentMap = new Dictionary < Node Node > (); // Populate parent map with DFS dfs ( root parentMap null ); // Find the nodes corresponding to // the values x and y Node p1 = findNode ( root x ); Node p2 = findNode ( root y ); // If nodes not found if ( p1 == null || p2 == null ) return - 1 ; // Sets to store nodes encountered // while traversing up the tree HashSet < Node > s1 = new HashSet < Node > (); HashSet < Node > s2 = new HashSet < Node > (); // Variable to store the maximum element // in the path int maxElement = int . MinValue ; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while ( p1 != p2 ) { if ( p1 != null ) { s1 . Add ( p1 ); maxElement = Math . Max ( maxElement p1 . data ); // Move to parent node p1 = parentMap [ p1 ]; } if ( p2 != null ) { s2 . Add ( p2 ); maxElement = Math . Max ( maxElement p2 . data ); p2 = parentMap [ p2 ]; } // Check if there's a common node in both sets if ( s1 . Contains ( p2 )) break ; if ( s2 . Contains ( p1 )) break ; } // Now both p1 and p2 point to their Lowest // Common Ancestor (LCA) maxElement = Math . Max ( maxElement p1 . data ); return maxElement ; } static void Main () { int [] arr = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; int n = arr . Length ; Node root = new Node ( arr [ 0 ]); for ( int i = 1 ; i < n ; i ++ ) insertNode ( root arr [ i ]); Console . WriteLine ( findMaxElement ( root a b )); } }
JavaScript // JavaScript program to find the maximum element in the path // between two Nodes of Binary Search Tree. class Node { constructor ( x ) { this . data = x ; this . left = this . right = null ; } } // Insert a new Node in Binary Search Tree function insertNode ( root x ) { let current = root parent = null ; // Traverse to the correct position for insertion while ( current !== null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct position if ( parent === null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // DFS to populate parent map for each node function dfs ( root parentMap parent = null ) { if ( root === null ) return ; // Store the parent of the current node if ( parent !== null ) { parentMap . set ( root parent ); } // Recur for left and right children dfs ( root . left parentMap root ); dfs ( root . right parentMap root ); } // Function to find the node with the given // value in the BST function findNode ( root val ) { if ( root === null ) return null ; if ( root . data === val ) return root ; let leftResult = findNode ( root . left val ); if ( leftResult !== null ) return leftResult ; return findNode ( root . right val ); } // Find maximum element in the path // between two nodes in BST function findMaxElement ( root x y ) { let parentMap = new Map (); // Populate parent map with DFS dfs ( root parentMap ); // Find the nodes corresponding to the // values x and y let p1 = findNode ( root x ); let p2 = findNode ( root y ); // If nodes not found if ( p1 === null || p2 === null ) return - 1 ; // Sets to store nodes encountered let s1 = new Set (); let s2 = new Set (); // Variable to store the maximum // element in the path let maxElement = - Infinity ; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while ( p1 !== p2 ) { if ( p1 !== null ) { s1 . add ( p1 ); maxElement = Math . max ( maxElement p1 . data ); // Move to parent node p1 = parentMap . get ( p1 ); } if ( p2 !== null ) { s2 . add ( p2 ); maxElement = Math . max ( maxElement p2 . data ); p2 = parentMap . get ( p2 ); } // Check if there's a common node in both sets if ( s1 . has ( p2 )) break ; if ( s2 . has ( p1 )) break ; } // Now both p1 and p2 point to their Lowest // Common Ancestor (LCA) maxElement = Math . max ( maxElement p1 . data ); return maxElement ; } let arr = [ 18 36 9 6 12 10 1 8 ]; let a = 1 b = 10 ; let n = arr . length ; let root = new Node ( arr [ 0 ]); for ( let i = 1 ; i < n ; i ++ ) insertNode ( root arr [ i ]); console . log ( findMaxElement ( root a b ));
Uitvoer
12
[Verwachte aanpak] Met behulp van LCA van twee knooppunten: O(h) Tijd en O(h) Ruimte
Het idee is om te vinden Laagste gemeenschappelijke voorouder van knooppunt 'a' en knooppunt 'b'. Zoek vervolgens het maximale knooppunt tussen LCA en 'a' en vind ook het maximale knooppunt tussen LCA en 'b'. Het antwoord is maximaal knooppunt twee.
Hieronder ziet u de implementatie van het bovenstaande algoritme:
C++ // C++ program to find maximum element in the path // between two Nodes of Binary Search Tree. #include using namespace std ; class Node { public : Node * left * right ; int data ; Node ( int x ) { data = x ; left = right = nullptr ; } }; // Insert a new Node in Binary Search Tree. void insertNode ( struct Node * root int x ) { Node * current = root * parent = nullptr ; while ( current != nullptr ) { parent = current ; if ( current -> data < x ) current = current -> right ; else current = current -> left ; } if ( parent == nullptr ) current = new Node ( x ); else { if ( parent -> data < x ) parent -> right = new Node ( x ); else parent -> left = new Node ( x ); } } // Return the maximum element between a Node // and its given ancestor. int maxelpath ( Node * root int x ) { Node * current = root ; int mx = INT_MIN ; // Traversing the path between ancestor and // Node and finding maximum element. while ( current -> data != x ) { if ( current -> data > x ) { mx = max ( mx current -> data ); current = current -> left ; } else { mx = max ( mx current -> data ); current = current -> right ; } } return max ( mx x ); } // Return maximum element in the path between // two given Node of BST. int maximumElement ( Node * root int x int y ) { Node * current = root ; // Finding the LCA of Node x and Node y while (( x < current -> data && y < current -> data ) || ( x > current -> data && y > current -> data )) { // Checking if both the Node lie on the // left side of the parent p. if ( x < current -> data && y < current -> data ) current = current -> left ; // Checking if both the Node lie on the // right side of the parent p. else if ( x > current -> data && y > current -> data ) current = current -> right ; } // Return the maximum of maximum elements occur // in path from ancestor to both Node. return max ( maxelpath ( current x ) maxelpath ( current y )); } int main () { int arr [] = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); Node * root = new Node ( arr [ 0 ]); for ( int i = 1 ; i < n ; i ++ ) insertNode ( root arr [ i ]); cout < < maximumElement ( root a b ) < < endl ; return 0 ; }
Java // Java program to find maximum element in the path // between two Nodes of Binary Search Tree. import java.util.* ; class Node { int data ; Node left right ; Node ( int x ) { data = x ; left = right = null ; } } class GfG { // Insert a new Node in Binary Search Tree static void insertNode ( Node root int x ) { Node current = root parent = null ; // Traverse to the correct // position for insertion while ( current != null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct // position if ( parent == null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // Find maximum element in the path from // an ancestor to a node static int maxInPath ( Node root int x ) { int maxElement = Integer . MIN_VALUE ; Node current = root ; // Traverse the path from root to the // target node 'x' while ( current != null && current . data != x ) { maxElement = Math . max ( maxElement current . data ); if ( x < current . data ) current = current . left ; else current = current . right ; } return Math . max ( maxElement x ); } // Find maximum element in the path between two // nodes in BST static int findMaxElement ( Node root int x int y ) { Node current = root ; // Find Lowest Common Ancestor (LCA) of x and y while (( x < current . data && y < current . data ) || ( x > current . data && y > current . data )) { if ( x < current . data && y < current . data ) current = current . left ; else if ( x > current . data && y > current . data ) current = current . right ; } // Find maximum elements in paths from LCA // to x and LCA to y return Math . max ( maxInPath ( current x ) maxInPath ( current y )); } public static void main ( String [] args ) { int [] arr = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; Node root = new Node ( arr [ 0 ] ); for ( int i = 1 ; i < arr . length ; i ++ ) insertNode ( root arr [ i ] ); System . out . println ( findMaxElement ( root a b )); } }
Python # Python program to find maximum element in the path # between two Nodes of Binary Search Tree. class Node : def __init__ ( self x ): self . data = x self . left = None self . right = None # Insert a new Node in Binary Search Tree def insertNode ( root x ): current = root parent = None # Traverse to the correct position for insertion while current is not None : parent = current if x < current . data : current = current . left else : current = current . right # Insert new Node at the correct position if parent is None : root = Node ( x ) elif x < parent . data : parent . left = Node ( x ) else : parent . right = Node ( x ) # Find maximum element in the path from an # ancestor to a node def maxInPath ( root x ): maxElement = float ( '-inf' ) current = root # Traverse the path from root to the # target node 'x' while current is not None and current . data != x : maxElement = max ( maxElement current . data ) if x < current . data : current = current . left else : current = current . right return max ( maxElement x ) # Find maximum element in the path between # two nodes in BST def findMaxElement ( root x y ): current = root # Find Lowest Common Ancestor (LCA) of x and y while ( x < current . data and y < current . data ) or ( x > current . data and y > current . data ): if x < current . data and y < current . data : current = current . left elif x > current . data and y > current . data : current = current . right # Find maximum elements in paths from LCA to # x and LCA to y return max ( maxInPath ( current x ) maxInPath ( current y )) if __name__ == '__main__' : arr = [ 18 36 9 6 12 10 1 8 ] a b = 1 10 root = Node ( arr [ 0 ]) for i in range ( 1 len ( arr )): insertNode ( root arr [ i ]) print ( findMaxElement ( root a b ))
C# // C# program to find maximum element in the path // between two Nodes of Binary Search Tree. using System ; class Node { public int data ; public Node left right ; public Node ( int x ) { data = x ; left = right = null ; } } class GfG { // Insert a new Node in Binary Search Tree static void insertNode ( Node root int x ) { Node current = root parent = null ; // Traverse to the correct position // for insertion while ( current != null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct position if ( parent == null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // Find maximum element in the path from an // ancestor to a node static int maxInPath ( Node root int x ) { int maxElement = int . MinValue ; Node current = root ; // Traverse the path from root to the target node 'x' while ( current != null && current . data != x ) { maxElement = Math . Max ( maxElement current . data ); if ( x < current . data ) current = current . left ; else current = current . right ; } return Math . Max ( maxElement x ); } // Find maximum element in the path between two nodes in BST static int findMaxElement ( Node root int x int y ) { Node current = root ; // Find Lowest Common Ancestor (LCA) of x and y while (( x < current . data && y < current . data ) || ( x > current . data && y > current . data )) { if ( x < current . data && y < current . data ) current = current . left ; else if ( x > current . data && y > current . data ) current = current . right ; } // Find maximum elements in paths from // LCA to x and LCA to y return Math . Max ( maxInPath ( current x ) maxInPath ( current y )); } static void Main () { int [] arr = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; Node root = new Node ( arr [ 0 ]); for ( int i = 1 ; i < arr . Length ; i ++ ) insertNode ( root arr [ i ]); Console . WriteLine ( findMaxElement ( root a b )); } }
JavaScript // JavaScript program to find maximum element in the path // between two Nodes of Binary Search Tree. class Node { constructor ( x ) { this . data = x ; this . left = null ; this . right = null ; } } // Insert a new Node in Binary Search Tree function insertNode ( root x ) { let current = root parent = null ; // Traverse to the correct position for insertion while ( current !== null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct position if ( parent === null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // Find maximum element in the path from an // ancestor to a node function maxInPath ( root x ) { let maxElement = - Infinity ; let current = root ; // Traverse the path from root to the target node 'x' while ( current !== null && current . data !== x ) { maxElement = Math . max ( maxElement current . data ); if ( x < current . data ) current = current . left ; else current = current . right ; } return Math . max ( maxElement x ); } // Find maximum element in the path between // two nodes in BST function findMaxElement ( root x y ) { let current = root ; // Find Lowest Common Ancestor (LCA) of x and y while (( x < current . data && y < current . data ) || ( x > current . data && y > current . data )) { if ( x < current . data && y < current . data ) current = current . left ; else if ( x > current . data && y > current . data ) current = current . right ; } // Find maximum elements in paths from LCA to // x and LCA to y return Math . max ( maxInPath ( current x ) maxInPath ( current y )); } const arr = [ 18 36 9 6 12 10 1 8 ]; const a = 1 b = 10 ; const root = new Node ( arr [ 0 ]); for ( let i = 1 ; i < arr . length ; i ++ ) { insertNode ( root arr [ i ]); } console . log ( findMaxElement ( root a b ));
Uitvoer
12Quiz maken







![Hond vastgeketend aan de voorkant van een huis in Texas Het water loopt tot aan haar hoofd [RESCUE VIDEO]](https://techcodeview.com/img/trending/65/dog-chained-to-front-of-house-in-texas-flood-waters-up-to-her-head-rescue-video.webp)