Deze tutorial is een beginnersvriendelijke gids voor het leren van datastructuren en algoritmen met behulp van Python. In dit artikel bespreken we de ingebouwde datastructuren zoals lijsten, tupels, woordenboeken, enz., en enkele door de gebruiker gedefinieerde datastructuren zoals gekoppelde lijsten , bomen , grafieken , etc, en doorloop-, zoek- en sorteeralgoritmen met behulp van goede en goed uitgelegde voorbeelden en oefenvragen.

Lijsten

Python-lijsten zijn geordende gegevensverzamelingen, net als arrays in andere programmeertalen. Het maakt verschillende soorten elementen in de lijst mogelijk. De implementatie van Python List is vergelijkbaar met vectoren in C++ of ArrayList in JAVA. De kostbare operatie is het invoegen of verwijderen van het element vanaf het begin van de lijst, omdat alle elementen moeten worden verschoven. Het invoegen en verwijderen aan het einde van de lijst kan ook kostbaar worden in het geval dat het vooraf toegewezen geheugen vol raakt.

Voorbeeld: Python-lijst maken

List = [1, 2, 3, 'GFG', 2.3] print(List) 

[1, 2, 3, 'GFG', 2.3] 

Lijstelementen zijn toegankelijk via de toegewezen index. In de startindex van Python van de lijst is een reeks 0 en de eindindex is (als er N elementen zijn) N-1.

Voorbeeld: Python-lijstbewerkingen

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3]) 

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks 

Tupel

Python-tupels zijn vergelijkbaar met lijsten, maar Tupels zijn dat wel onveranderlijk in de natuur, d.w.z. eenmaal gecreëerd, kan het niet meer worden gewijzigd. Net als een lijst kan een Tuple ook elementen van verschillende typen bevatten.

In Python worden tupels gemaakt door een reeks waarden te plaatsen, gescheiden door ‘komma’, met of zonder het gebruik van haakjes voor het groeperen van de gegevensreeks.

Opmerking: Om een ​​tuple van één element te maken, moet er een afsluitende komma staan. Met (8,) wordt bijvoorbeeld een tupel gemaakt die 8 als element bevat.

Voorbeeld: Python Tuple-bewerkingen

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3]) 

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 

Set

Python-set is een veranderlijke verzameling gegevens die geen enkele duplicatie toestaat. Sets worden in principe gebruikt om lidmaatschapstests uit te voeren en dubbele vermeldingen te elimineren. De datastructuur die hierbij wordt gebruikt is Hashing, een populaire techniek om gemiddeld invoeging, verwijdering en traversal in O(1) uit te voeren.

Als er meerdere waarden aanwezig zijn op dezelfde indexpositie, wordt de waarde aan die indexpositie toegevoegd om een ​​gekoppelde lijst te vormen. Hierin worden CPython-sets geïmplementeerd met behulp van een woordenboek met dummyvariabelen, waarbij sleutelwezens door de leden worden ingesteld met grotere optimalisaties van de tijdscomplexiteit.

Implementatie instellen:

Sets met talloze bewerkingen op één enkele hashtabel:

Voorbeeld: Python Set-bewerkingen

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set) 

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True 

Bevroren sets

Bevroren sets in Python zijn onveranderlijke objecten die alleen methoden en operatoren ondersteunen die een resultaat opleveren zonder de bevroren set of sets waarop ze worden toegepast te beïnvloeden. Hoewel elementen van een set op elk moment kunnen worden gewijzigd, blijven elementen van de bevroren set na het maken hetzelfde.

Voorbeeld: Python Frozen-set

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h') 

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'}) 

Snaar

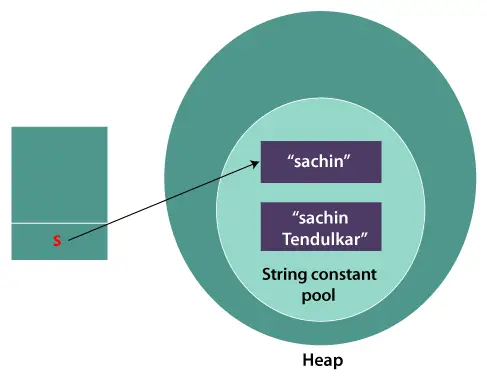
Python-snaren is de onveranderlijke reeks bytes die Unicode-tekens vertegenwoordigen. Python heeft geen tekengegevenstype, een enkel teken is eenvoudigweg een string met een lengte van 1.

Opmerking: Omdat strings onveranderlijk zijn, zal het wijzigen van een string resulteren in het maken van een nieuwe kopie.

Voorbeeld: Python Strings-bewerkingen

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1]) 

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s 

Woordenboek

Python-woordenboek is een ongeordende verzameling gegevens waarin gegevens worden opgeslagen in de indeling sleutel:waardepaar. Het is net als hashtabellen in elke andere taal met de tijdscomplexiteit van O(1). Het indexeren van Python Dictionary gebeurt met behulp van sleutels. Deze zijn van elk hashbaar type, dat wil zeggen een object dat nooit kan veranderen, zoals tekenreeksen, getallen, tupels, enz. We kunnen een woordenboek maken door accolades ({}) of woordenboekbegrip te gebruiken.

Voorbeeld: Python-woordenboekbewerkingen

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict) 

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} 

Matrix

Een matrix is ​​een 2D-array waarbij elk element strikt dezelfde grootte heeft. Om een ​​matrix te maken, gebruiken we de NumPy-pakket .

Voorbeeld: Python NumPy-matrixbewerkingen

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m) 

Uitvoer

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] 

Bytearray

Python Bytearray geeft een veranderlijke reeks gehele getallen in het bereik 0 <= x < 256.

Voorbeeld: Python Bytearray-bewerkingen

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a) 

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e') 

Gekoppelde lijst

A gekoppelde lijst is een lineaire datastructuur, waarbij de elementen niet op aangrenzende geheugenlocaties worden opgeslagen. De elementen in een gekoppelde lijst zijn gekoppeld met behulp van verwijzingen, zoals weergegeven in de onderstaande afbeelding:

Een gekoppelde lijst wordt weergegeven door een verwijzing naar het eerste knooppunt van de gekoppelde lijst. Het eerste knooppunt wordt het hoofd genoemd. Als de gekoppelde lijst leeg is, is de waarde van het hoofd NULL. Elk knooppunt in een lijst bestaat uit minimaal twee delen:

• Gegevens
• Wijzer (of referentie) naar het volgende knooppunt

Voorbeeld: gekoppelde lijst definiëren in Python

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None 

Laten we een eenvoudige gekoppelde lijst maken met 3 knooppunten.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | nul | | 3 | nul |  +----+------+ +----+------+ +----+-----+ ''' tweede.volgende = derde ; # Koppel het tweede knooppunt met het derde knooppunt ''' Nu verwijst het volgende van het tweede knooppunt naar het derde knooppunt. Alle drie de knooppunten zijn dus met elkaar verbonden.  llist.head tweede derde | | |  | | |  +----+------+ +----+------+ +----+-----+ | 1 | o-------->| 2 | o-------->| 3 | nul |  +----+------+ +----+------+ +----+------+ ''' 

Gekoppelde lijstdoorgang

In het vorige programma hebben we een eenvoudige gekoppelde lijst met drie knooppunten gemaakt. Laten we de gemaakte lijst doorkruisen en de gegevens van elk knooppunt afdrukken. Laten we voor het doorlopen een algemene functie printList() schrijven die een bepaalde lijst afdrukt.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList() 

1 2 3 

Meer artikelen op gelinkte lijst

• Gekoppelde lijstinvoeging
• Gekoppelde lijst verwijderen (een bepaalde sleutel verwijderen)
• Gekoppelde lijst verwijderen (een sleutel op een bepaalde positie verwijderen)
• Zoek de lengte van een gekoppelde lijst (iteratief en recursief)
• Een element zoeken in een gekoppelde lijst (iteratief en recursief)
• N-de knooppunt vanaf het einde van een gekoppelde lijst
• Een gekoppelde lijst omkeren

A stapel is een lineaire datastructuur die items opslaat op een Last-In/First-Out (LIFO) of First-In/Last-Out (FILO) manier. Bij stapelen wordt aan één uiteinde een nieuw element toegevoegd en alleen aan dat uiteinde wordt een element verwijderd. De invoeg- en verwijderbewerkingen worden vaak push en pop genoemd.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty 

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: [] 

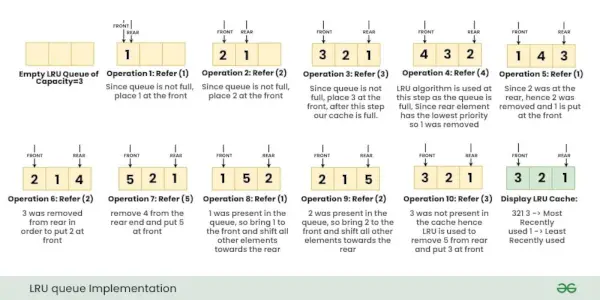
Als stapel wordt de wachtrij is een lineaire datastructuur waarin items op een First In First Out (FIFO) manier worden opgeslagen. Bij een wachtrij wordt het minst recent toegevoegde item als eerste verwijderd. Een goed voorbeeld van de wachtrij is elke wachtrij van consumenten voor een hulpbron waarbij de consument die als eerste kwam, als eerste wordt bediend.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty 

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements [] 

Prioritaire wachtrijen zijn abstracte datastructuren waarbij elke data/waarde in de wachtrij een bepaalde prioriteit heeft. Bij luchtvaartmaatschappijen komt bagage met de titel Business of First Class bijvoorbeeld eerder aan dan de rest. Prioriteitswachtrij is een uitbreiding van de wachtrij met de volgende eigenschappen.

• Een element met hoge prioriteit wordt uit de wachtrij gehaald vóór een element met lage prioriteit.
• Als twee elementen dezelfde prioriteit hebben, worden ze geserveerd volgens hun volgorde in de wachtrij.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] retourneert item behalve IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) terwijl niet myQueue.isEmpty(): print(myQueue.delete()) 

12 1 14 7 14 12 7 1 

Hoop

heapq-module in Python biedt de heap-gegevensstructuur die voornamelijk wordt gebruikt om een ​​prioriteitswachtrij weer te geven. De eigenschap van deze datastructuur is dat deze altijd het kleinste element (min heap) oplevert wanneer het element wordt gepopt. Telkens wanneer elementen worden geduwd of gepoft, blijft de heap-structuur behouden. Het element heap[0] retourneert ook elke keer het kleinste element. Het ondersteunt de extractie en invoeging van het kleinste element in de O(log n) tijden.

Over het algemeen kunnen Heaps uit twee typen bestaan:

• Max-hoop: In een Max-Heap moet de sleutel die aanwezig is op het hoofdknooppunt de grootste zijn van de sleutels die aanwezig zijn bij alle onderliggende knooppunten. Dezelfde eigenschap moet recursief waar zijn voor alle subbomen in die binaire boom.
• Min-hoop: In een Min-Heap moet de sleutel die aanwezig is op het hoofdknooppunt minimaal zijn onder de sleutels die aanwezig zijn bij alle onderliggende knooppunten. Dezelfde eigenschap moet recursief waar zijn voor alle subbomen in die binaire boom.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li)) 

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1 

Meer artikelen over Heap

• Binaire hoop
• K'th grootste element in een array
• K'th Kleinste/grootste element in ongesorteerde array
• Sorteer een bijna gesorteerde array
• K-de grootste som aaneengesloten subarray
• Minimale som van twee getallen gevormd uit cijfers van een array

Een boom is een hiërarchische gegevensstructuur die eruitziet als de onderstaande afbeelding:

 tree  ----  j  <-- root  /   f k  /   a h z  <-- leaves 

Het bovenste knooppunt van de boom wordt de wortel genoemd, terwijl de onderste knooppunten of de knooppunten zonder kinderen de bladknooppunten worden genoemd. De knooppunten die zich direct onder een knooppunt bevinden, worden de onderliggende knooppunten genoemd, en de knooppunten die zich direct boven iets bevinden, worden de ouder genoemd.

A binaire boom is een boom waarvan de elementen bijna twee kinderen kunnen hebben. Omdat elk element in een binaire boom slechts twee kinderen kan hebben, noemen we ze doorgaans de linker- en rechterkinderen. Een Binary Tree-knooppunt bevat de volgende onderdelen.

• Gegevens
• Wijzer naar het linkerkind
• Wijzer naar het juiste kind

Voorbeeld: knooppuntklasse definiëren

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key 

Laten we nu een boom maken met 4 knooppunten in Python. Laten we aannemen dat de boomstructuur er als volgt uitziet:

 tree  ----  1  <-- root  /   2 3   /  4 

Voorbeeld: gegevens aan de boom toevoegen

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None''' 

Boomdoortocht

Bomen kunnen worden doorkruist op verschillende manieren. Hieronder volgen de algemeen gebruikte manieren om bomen te doorkruisen. Laten we de onderstaande boom bekijken -

 tree  ----  1  <-- root  /   2 3   /  4 5 

Diepte Eerste Traversals:

• In volgorde (links, wortel, rechts): 4 2 5 1 3
• Voorbestelling (Root, Links, Rechts): 1 2 4 5 3
• Postorder (links, rechts, root): 4 5 2 3 1

Algoritme in volgorde(boom)

• Doorloop de linker deelboom, d.w.z. roep Inorder(linker-subboom) aan
• Bezoek de wortel.
• Doorloop de rechter deelboom, d.w.z. roep Inorder(rechter-subboom) aan

Algoritme vooraf bestellen(boom)

• Bezoek de wortel.
• Doorloop de linker subboom, d.w.z. roep Preorder(linker-subboom) aan
• Doorloop de rechter subboom, d.w.z. roep Preorder(rechter-subboom) aan

Algoritme Postwissel(boom)

• Doorloop de linker subboom, d.w.z. roep Postorder(linker-subboom) aan
• Doorloop de rechter subboom, d.w.z. roep Postorder(rechter-subboom) aan
• Bezoek de wortel.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root) 

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1 

Tijdcomplexiteit – O(n)

Breedte-eerste of niveau-ordertransactie

Niveauvolgorde doorlopen van een boom is de breedte-eerste doorgang voor de boom. De niveauvolgorde van de bovenstaande boom is 1 2 3 4 5.

Voor elk knooppunt wordt het knooppunt eerst bezocht en vervolgens worden de onderliggende knooppunten in een FIFO-wachtrij geplaatst. Hieronder staat het algoritme voor hetzelfde -

• Maak een lege wachtrij q
• temp_node = root /*start vanaf root*/
• Loop terwijl temp_node niet NULL is
  • print temp_node->gegevens.
  • Plaats de kinderen van temp_node (eerst links en dan rechts) in de wachtrij voor q
  • Haal een knooppunt uit q uit de wachtrij

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Druk de voorkant van de wachtrij af en # verwijder deze uit de wachtrij print (queue[0].data) node = wachtrij.pop(0) # Zet het linker kind in de wachtrij als node.left niet Geen is: wachtrij.append(node.left ) # Rechts kind in wachtrij plaatsen als node.right niet Geen is: wachtrij.append(node.right) # Stuurprogramma om bovenstaande functie te testen root = Knooppunt(1) root.left = Knooppunt(2) root.right = Knooppunt(3) root.left.left = Knooppunt(4) root.left.right = Knooppunt(5) print ('Niveauvolgorde Traversal van binaire boom is -') printLevelOrder(root) 

Level Order Traversal of binary tree is - 1 2 3 4 5 

Tijdcomplexiteit: O(n)

Meer artikelen over binaire boom

• Invoeging in een binaire boom
• Verwijdering in een binaire boom
• Inorder Tree Traversal zonder recursie
• Inorder Tree Traversal zonder recursie en zonder stapel!
• Postorder-traversal afdrukken van bepaalde Inorder- en Pre-order-traversals
• Zoek postorder-traversal van BST uit pre-order-traversal

Binaire zoekboom is een op knooppunten gebaseerde binaire boomgegevensstructuur met de volgende eigenschappen:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val  < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key) 

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val  < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r) 

20 30 40 50 60 70 80 

A grafiek is een niet-lineaire datastructuur bestaande uit knooppunten en randen. De knooppunten worden ook wel hoekpunten genoemd en de randen zijn lijnen of bogen die twee willekeurige knooppunten in de grafiek met elkaar verbinden. Formeel kan een grafiek worden gedefinieerd als een grafiek die bestaat uit een eindige reeks hoekpunten (of knooppunten) en een reeks randen die een paar knooppunten verbinden.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0 <=vtx <=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix()) 

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Stuurprogramma voor de bovenstaande grafiekklasse als __name__ == '__main__' : V = 5 grafiek = Grafiek(V) grafiek.add_edge(0, 1) grafiek.add_edge(0, 4) grafiek.add_edge(1, 2) grafiek.add_edge(1, 3) grafiek.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph() 

Adjacency list of vertex 0 head ->4 -> 1 Aangrenzende lijst van hoekpunt 1 hoofd -> 4 -> 3 -> 2 -> 0 Aangrenzende lijst van hoekpunt 2 hoofd -> 3 -> 1 Aangrenzende lijst van hoekpunt 3 hoofd -> 4 -> 2 -> 1 Aangrenzende lijst lijst van hoekpunt 4 hoofd -> 3 -> 1 -> 0 

Breedte-eerste doorgang want een grafiek is vergelijkbaar met de breedte-eerste doorgang van een boom. Het enige probleem hier is dat grafieken, in tegenstelling tot bomen, cycli kunnen bevatten, waardoor we mogelijk weer op hetzelfde knooppunt terechtkomen. Om te voorkomen dat een knooppunt meerdere keren wordt verwerkt, gebruiken we een Booleaanse bezochte array. Voor de eenvoud wordt aangenomen dat alle hoekpunten bereikbaar zijn vanaf het startpunt.

In de volgende grafiek beginnen we bijvoorbeeld met het doorlopen van hoekpunt 2. Wanneer we bij hoekpunt 0 komen, zoeken we naar alle aangrenzende hoekpunten ervan. 2 is ook een aangrenzend hoekpunt van 0. Als we de bezochte hoekpunten niet markeren, wordt 2 opnieuw verwerkt en wordt het een niet-beëindigend proces. Een breedte-eerste doorgang van de volgende grafiek is 2, 0, 3, 1.

# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2) 

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1 

Tijdcomplexiteit: O(V+E) waarbij V het aantal hoekpunten in de grafiek is en E het aantal randen in de grafiek.

Diepte eerst zoeken of DFS

Diepte Eerste Traversal voor een grafiek is vergelijkbaar met Diepte Eerste Traversal van een boom. Het enige probleem hier is dat grafieken, in tegenstelling tot bomen, cycli kunnen bevatten en dat een knooppunt twee keer kan worden bezocht. Om te voorkomen dat een knooppunt meerdere keren wordt verwerkt, gebruikt u een Booleaanse bezochte array.

Algoritme:

• Maak een recursieve functie die de index van het knooppunt en een bezochte array overneemt.
• Markeer het huidige knooppunt als bezocht en druk het knooppunt af.
• Doorloop alle aangrenzende en ongemarkeerde knooppunten en roep de recursieve functie aan met de index van het aangrenzende knooppunt.

# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2) 

Following is DFS from (starting from vertex 2) 2 0 1 3 

Meer artikelen over grafiek

• Grafiekweergaven met behulp van set en hash
• Vind moederhoekpunt in een grafiek
• Iteratieve diepte eerste zoekopdracht
• Tel het aantal knooppunten op een bepaald niveau in een boom met behulp van BFS
• Tel alle mogelijke paden tussen twee hoekpunten

Het proces waarin een functie zichzelf direct of indirect aanroept, wordt recursie genoemd en de overeenkomstige functie wordt a genoemd recursieve functie . Met behulp van de recursieve algoritmen kunnen bepaalde problemen vrij eenvoudig worden opgelost. Voorbeelden van dergelijke problemen zijn Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, enz.

def fact(n):  # base case  if (n  <= 1)   return 1  else   return n*fact(n-1) 

# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test  < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test) 

3 2 1 1 2 3 

• Herhaling
• Recursie in Python
• Oefenvragen voor recursie | Set 1
• Oefenvragen voor recursie | Stel 2 in
• Oefenvragen voor recursie | Set 3
• Oefenvragen voor recursie | Set 4
• Oefenvragen voor recursie | Stel 5 in
• Oefenvragen voor recursie | Stel 6 in
• Oefenvragen voor recursie | Stel 7 in

>>> Meer

Dynamisch programmeren

Dynamisch programmeren is voornamelijk een optimalisatie via gewone recursie. Overal waar we een recursieve oplossing zien die herhaaldelijk om dezelfde invoer vraagt, kunnen we deze optimaliseren met behulp van dynamisch programmeren. Het idee is om de resultaten van deelproblemen eenvoudigweg op te slaan, zodat we ze later niet opnieuw hoeven te berekenen als dat nodig is. Deze eenvoudige optimalisatie reduceert de tijdscomplexiteit van exponentieel naar polynoom. Als we bijvoorbeeld een eenvoudige recursieve oplossing voor Fibonacci-getallen schrijven, krijgen we exponentiële tijdscomplexiteit en als we deze optimaliseren door oplossingen van deelproblemen op te slaan, wordt de tijdscomplexiteit teruggebracht tot lineair.

Tabelleren versus memoriseren

Er zijn twee verschillende manieren om de waarden op te slaan, zodat de waarden van een deelprobleem opnieuw kunnen worden gebruikt. Hier worden twee patronen voor het oplossen van dynamische programmeerproblemen (DP) besproken:

• Tabel: Onderkant boven
• Memoriseren: Ondersteboven

Tabel

Zoals de naam zelf suggereert, beginnend vanaf de onderkant en het verzamelen van antwoorden naar de top. Laten we het hebben over de staatstransitie.

Laten we een toestand voor ons DP-probleem beschrijven als dp[x] met dp[0] als basistoestand en dp[n] als onze bestemmingstoestand. We moeten dus de waarde van de bestemmingsstatus vinden, d.w.z. dp[n].

Als we onze transitie starten vanuit onze basistoestand, d.w.z. dp[0] en onze toestandstransitierelatie volgen om onze bestemmingstoestand dp[n] te bereiken, noemen we dit de Bottom-Up-benadering, omdat het vrij duidelijk is dat we onze transitie begonnen vanuit de onderste basisstatus en bereikte de bovenste gewenste staat.

Waarom noemen we dit de tabelleringsmethode?

Om dit te weten, gaan we eerst wat code schrijven om de faculteit van een getal te berekenen met behulp van een bottom-up benadering. Nogmaals, als algemene procedure om een ​​DP op te lossen, definiëren we eerst een staat. In dit geval definiëren we een toestand als dp[x], waarbij dp[x] de faculteit van x moet vinden.

Het is nu heel duidelijk dat dp[x+1] = dp[x] * (x+1)

# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i 

Memoriseren

Laten we het nogmaals beschrijven in termen van staatstransitie. Als we de waarde voor een bepaalde toestand moeten vinden, zeg dan dp[n] en in plaats van te vertrekken vanuit de basistoestand, d.w.z. dp[0], vragen we ons antwoord aan de toestanden die de bestemmingstoestand dp[n] kunnen bereiken na de toestandsovergang relatie, dan is het de top-down-mode van DP.

Hier beginnen we onze reis vanuit de bovenste bestemmingsstaat en berekenen het antwoord door de waarden te tellen van staten die de bestemmingsstaat kunnen bereiken, totdat we de onderste basisstaat bereiken.

Laten we de code voor het faculteitsprobleem nogmaals van bovenaf schrijven

# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1)) 

Meer artikelen over dynamisch programmeren

• Optimale onderbouweigenschap
• Overlappende deelproblemen Eigenschap
• Fibonacci-getallen
• Deelverzameling waarvan de som deelbaar is door m
• Maximale som toenemende vervolgvolgorde
• Langste gemeenschappelijke subtekenreeks

>>> Meer

Algoritmen zoeken

Lineair zoeken

• Begin met het meest linkse element van arr[] en vergelijk x één voor één met elk element van arr[]
• Als x overeenkomt met een element, retourneert u de index.
• Als x niet overeenkomt met een van de elementen, retourneert u -1.

# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result) 

Element is present at index 3 

De tijdscomplexiteit van het bovenstaande algoritme is O(n).

Voor meer informatie, zie Lineair zoeken .

Binaire zoekopdracht

Doorzoek een gesorteerde array door het zoekinterval herhaaldelijk doormidden te delen. Begin met een interval dat de hele array bestrijkt. Als de waarde van de zoeksleutel kleiner is dan het item in het midden van het interval, verkleint u het interval tot de onderste helft. Anders beperkt u het tot de bovenste helft. Controleer herhaaldelijk totdat de waarde is gevonden of het interval leeg is.

# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Als element aanwezig is in het midden zelf if arr[mid] == x: return mid # Als element kleiner is dan mid, dan kan het # alleen aanwezig zijn in linker subarray elif arr[mid]> x: return binarySearch(arr, l, mid-1, x) # Anders kan het element alleen aanwezig zijn # in rechter subarray else: return binarySearch(arr, mid + 1, r, x ) else: # Element is niet aanwezig in de array-retour -1 # Stuurprogrammacode arr = [ 2, 3, 4, 10, 40 ] x = 10 # Functieaanroepresultaat = binarySearch(arr, 0, len(arr)-1 , x) if resultaat != -1: print ('Element is aanwezig in index % d' % resultaat) else: print ('Element is niet aanwezig in array') 

Element is present at index 3 

De tijdscomplexiteit van het bovenstaande algoritme is O(log(n)).

Voor meer informatie, zie Binaire zoekopdracht .

Sorteeralgoritmen

Selectie Sorteren

De selectie sorteren algoritme sorteert een array door herhaaldelijk het minimumelement (rekening houdend met oplopende volgorde) uit het ongesorteerde deel te vinden en dit aan het begin te plaatsen. Bij elke iteratie van selectiesortering wordt het minimumelement (rekening houdend met de oplopende volgorde) uit de ongesorteerde subarray gekozen en verplaatst naar de gesorteerde subarray.

Stroomdiagram van de selectiesortering:

# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Verwissel het gevonden minimumelement met # het eerste element A[i], A[min_idx] = A[min_idx], A[i] # Stuurprogrammacode om te testen hierboven print ('Gesorteerde array ') voor i binnen bereik(len(A)): print('%d' %A[i]), 

Sorted array 11 12 22 25 64 

Tijdcomplexiteit: Op ² ) omdat er twee geneste lussen zijn.

Hulpruimte: O(1)

Bellen sorteren

Bellen sorteren is het eenvoudigste sorteeralgoritme dat werkt door de aangrenzende elementen herhaaldelijk om te wisselen als ze in de verkeerde volgorde staan.

Illustratie:

# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Stuurprogrammacode om hierboven te testen arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Gesorteerde array is:') voor i binnen bereik(len(arr)): print ('%d' %arr[i]), 

Sorted array is: 11 12 22 25 34 64 90 

Tijdcomplexiteit: Op ² )

Invoegsortering

Om een ​​array met grootte n in oplopende volgorde te sorteren met behulp van invoegsoort :

• Herhaal van arr[1] naar arr[n] over de array.
• Vergelijk het huidige element (sleutel) met zijn voorganger.
• Als het sleutelelement kleiner is dan zijn voorganger, vergelijk het dan met de voorgaande elementen. Verplaats de grotere elementen één positie naar boven om ruimte te maken voor het verwisselde element.

Illustratie:

# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 en sleutel < arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i]) 

 5 6 11 12 13 

Tijdcomplexiteit: Op ² ))

Sortering samenvoegen

Net als QuickSort, Sortering samenvoegen is een verdeel en heers-algoritme. Het verdeelt de invoerarray in twee helften, roept zichzelf op voor de twee helften en voegt vervolgens de twee gesorteerde helften samen. De merge() functie wordt gebruikt voor het samenvoegen van twee helften. De merge(arr, l, m, r) is een sleutelproces dat ervan uitgaat dat arr[l..m] en arr[m+1..r] zijn gesorteerd en de twee gesorteerde subarrays samenvoegt tot één.

MergeSort(arr[], l, r) If r>l 1. Zoek het middelpunt om de array in twee helften te verdelen: middelste m = l+ (r-l)/2 2. Roep mergeSort aan voor de eerste helft: Roep mergeSort(arr, l, m) aan 3. Roep mergeSort aan voor de tweede helft: Roep mergeSort(arr, m+1, r) 4. Voeg de twee helften samen, gesorteerd in stap 2 en 3: Roep merge(arr, l, m, r)>'> aan   
     
Python3   
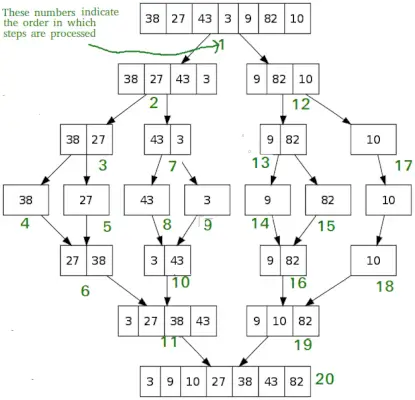
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Het midden van de array vinden mid = len(arr)//2 # De array-elementen verdelen L = arr[:mid] # in 2 helften R = arr[mid:] # De eerste helft sorteren mergeSort(L) # Sorteren van de tweede helft mergeSort(R) i = j = k = 0 # Kopieer gegevens naar tijdelijke arrays L[] en R[] terwijl i < len(L) and j  < len(R): if L[i]  < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i  < len(L): arr[k] = L[i] i += 1 k += 1 while j  < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr) 
    
  Uitvoer       Tijdcomplexiteit:     O(n(log))  
  
 Snel sorteren  
 
 Zoals samenvoegen en sorteren,    Snel sorteren    is een verdeel en heers-algoritme. Het kiest een element als draaipunt en verdeelt de gegeven array rond het gekozen draaipunt. Er zijn veel verschillende versies van quickSort die op verschillende manieren een draaipunt kiezen.  
  
 Kies altijd het eerste element als draaipunt.  
  
 
 Kies altijd het laatste element als spil (hieronder geïmplementeerd)  
 
 Kies een willekeurig element als draaipunt.  
 
 Kies de mediaan als draaipunt.  
 
 
 Het belangrijkste proces in quickSort is partitie(). Het doel van partities is, gegeven een array en een element x van array als draaipunt, x op de juiste positie in de gesorteerde array plaatsen en alle kleinere elementen (kleiner dan x) vóór x plaatsen, en alle grotere elementen (groter dan x) erna plaatsen X. Dit alles zou in lineaire tijd moeten gebeuren.  
  
/* low -->Startindex, hoog --> Eindindex */ quickSort(arr[], low, high) { if (low { /* pi is de partitie-index, arr[pi] staat nu op de juiste plaats */ pi = partitie(arr, laag, hoog); quickSort(arr, laag, pi - 1); // Vóór pi quickSort(arr, pi + 1, hoog);  
  
  
    Partitie-algoritme     
  
 Er kunnen veel manieren zijn om partities uit te voeren, als volgt    pseudo-code    hanteert de methode uit het CLRS-boek. De logica is eenvoudig: we beginnen met het meest linkse element en houden de index van kleinere (of gelijk aan) elementen bij als i. Als we tijdens het doorkruisen een kleiner element vinden, wisselen we het huidige element om met arr[i]. Anders negeren we het huidige element.  
  pivot: end -= 1 # Als begin en einde elkaar niet hebben gekruist, # verwissel de getallen bij begin en einde if(start < end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start  < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}') 
    
  Uitvoer   
Sorted array: [1, 5, 7, 8, 9, 10] 
  
    Tijdcomplexiteit:     O(n(log))  
  
 ShellSort  
 
  ShellSort   is voornamelijk een variant van Insertion Sort. Bij invoegsortering verplaatsen we elementen slechts één positie vooruit. Wanneer een element ver vooruit moet worden bewogen, zijn er veel bewegingen nodig. Het idee van shellSort is om de uitwisseling van verre items mogelijk te maken. In shellSort maken we de array h-gesorteerd voor een grote waarde van h. We blijven de waarde van h verlagen totdat deze 1 wordt. Er wordt gezegd dat een array h-gesorteerd is als alle sublijsten van elke h   e   element is gesorteerd.  
Python3   
# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = gap # controleer de array van links naar rechts # tot de laatst mogelijke index van j terwijl j < len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # nu kijken we terug van de i-de index naar links # we wisselen de waarden om die staan ​​niet in de juiste volgorde. k = i terwijl k - tussenruimte> -1: als arr[k - tussenruimte]> arr[k]: arr[k-tussenruimte],arr[k] = arr[k],arr[k-tussenruimte] k -= 1 gap //= 2 # driver om de code te controleren arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2) 
    
  Uitvoer   
input array: [12, 34, 54, 2, 3] sorted array [2, 3, 12, 34, 54] 
  
    Tijdcomplexiteit:     Op   2   ).