INORDER TRAVERSAL VAN BINAIRE BOOM

In volgorde doorkruisen wordt gedefinieerd als een soort techniek van het doorkruisen van bomen die het links-wortel-rechts-patroon volgt, zodat:

De linker deelboom wordt als eerste doorlopen

Vervolgens wordt het hoofdknooppunt voor die subboom doorlopen

Ten slotte wordt de rechter deelboom doorlopen

In volgorde doorkruisen

Algoritme voor ongeordende doorgang van binaire boom

Het algoritme voor inorder-traversal wordt als volgt weergegeven:

In volgorde(wortel):

Volg stap 2 tot en met 4 tot root != NULL

In volgorde (wortel -> links)

Schrijf root -> gegevens

In volgorde (wortel -> rechts)

Einde lus

Hoe werkt Inorder Traversal of Binary Tree?

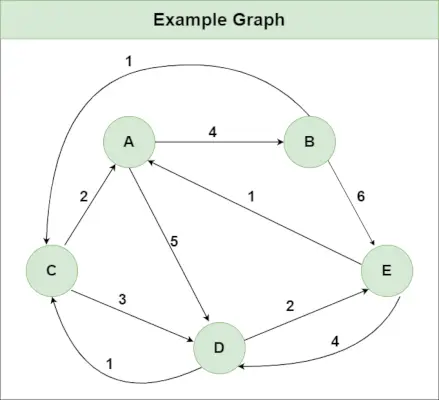
Beschouw de volgende boom:

Voorbeeld van binaire boom

Als we een niet-geordende verplaatsing in deze binaire boom uitvoeren, zal de verplaatsing als volgt zijn:

Stap 1: De verplaatsing gaat van 1 naar de linker deelboom, d.w.z. 2, en vervolgens van 2 naar de wortel van de linker deelboom, d.w.z. 4. Nu heeft 4 geen linker deelboom, dus deze zal worden bezocht. Het heeft ook geen juiste subboom. Dus geen verplaatsing meer vanaf 4

Knooppunt 4 wordt bezocht

Stap 2: Omdat de linker subboom van 2 volledig is bezocht, leest het nu de gegevens van knooppunt 2 voordat het naar de rechter subboom gaat.

Knooppunt 2 wordt bezocht

Stap 3: Nu zal de rechter deelboom van 2 worden doorlopen, d.w.z. ga naar knooppunt 5. Voor knooppunt 5 is er geen linker deelboom, dus deze wordt bezocht en daarna komt de doorgang terug omdat er geen rechter deelboom van knooppunt 5 is.

Knooppunt 5 wordt bezocht

Stap 4: Zoals de linker subboom van knooppunt 1 is, zal de wortel zelf, d.w.z. knooppunt 1, worden bezocht.

Knooppunt 1 wordt bezocht

Stap 5: Linker deelboom van knooppunt 1 en het knooppunt zelf worden bezocht. Dus nu zal de rechter deelboom van 1 worden doorlopen, d.w.z. ga naar knooppunt 3. Omdat knooppunt 3 geen linker deelboom heeft, wordt deze bezocht.

Knooppunt 3 wordt bezocht

Stap 6: De linker deelboom van knooppunt 3 en het knooppunt zelf worden bezocht. Ga dus naar de rechter subboom en bezoek knooppunt 6. Nu eindigt de verplaatsing omdat alle knooppunten zijn doorlopen.

De volledige boom wordt doorkruist

De volgorde van het doorlopen van knooppunten is dus 4 -> 2 -> 5 -> 1 -> 3 -> 6 .

Programma om Inorder Traversal of Binary Tree te implementeren:

Hieronder vindt u de code-implementatie van de inorder-traversal:

C++

// C++ program for inorder traversals> #include> using> namespace> std;> // Structure of a Binary Tree Node> struct> Node {> > int> data;> > struct> Node *left, *right;> > Node(> int> v)> > {> > data = v;> > left = right = NULL;> > }> };> // Function to print inorder traversal> void> printInorder(> struct> Node* node)> {> > if> (node == NULL)> > return> ;> > // First recur on left subtree> > printInorder(node->links);> > // Now deal with the node> >

cout ' ';  // Then recur on right subtree  printInorder(node->rechts); } // Stuurprogrammacode int main() { struct Node* root = new Node(1);  root->left = nieuw knooppunt(2);  root->right = nieuw knooppunt(3);  root->left->left = nieuw knooppunt(4);  root->links->rechts = nieuw knooppunt(5);  root->right->right = nieuw knooppunt(6);  // Functieoproep cout < < 'Inorder traversal of binary tree is: 
';  printInorder(root);  return 0; }>

Java

// Java program for inorder traversals> import> java.util.*;> // Structure of a Binary Tree Node> class> Node {> > int> data;> > Node left, right;> > Node(> int> v)> > {> > data = v;> > left = right => null> ;> > }> }> // Main class> class> GFG {> > // Function to print inorder traversal> > public> static> void> printInorder(Node node)> > {> > if> (node ==> null> )> > return> ;> > // First recur on left subtree> > printInorder(node.left);> > // Now deal with the node> > System.out.print(node.data +> ' '> );> > // Then recur on right subtree> > printInorder(node.right);> > }> > // Driver code> > public> static> void> main(String[] args)> > {> > Node root => new> Node(> 1> );> > root.left => new> Node(> 2> );> > root.right => new> Node(> 3> );> > root.left.left => new> Node(> 4> );> > root.left.right => new> Node(> 5> );> > root.right.right => new> Node(> 6> );> > // Function call> > System.out.println(> > 'Inorder traversal of binary tree is: '> );> > printInorder(root);> > }> }> // This code is contributed by prasad264>

Python3

# Structure of a Binary Tree Node> class> Node:> > def> __init__(> self> , v):> > self> .data> => v> > self> .left> => None> > self> .right> => None> # Function to print inorder traversal> def> printInorder(node):> > if> node> is> None> :> > return> > # First recur on left subtree> > printInorder(node.left)> > # Now deal with the node> > print> (node.data, end> => ' '> )> > # Then recur on right subtree> > printInorder(node.right)> # Driver code> if> __name__> => => '__main__'> :> > root> => Node(> 1> )> > root.left> => Node(> 2> )> > root.right> => Node(> 3> )> > root.left.left> => Node(> 4> )> > root.left.right> => Node(> 5> )> > root.right.right> => Node(> 6> )> > # Function call> > print> (> 'Inorder traversal of binary tree is:'> )> > printInorder(root)>

C#

// C# program for inorder traversals> using> System;> // Structure of a Binary Tree Node> public> class> Node {> > public> int> data;> > public> Node left, right;> > public> Node(> int> v)> > {> > data = v;> > left = right => null> ;> > }> }> // Class to store and print inorder traversal> public> class> BinaryTree {> > // Function to print inorder traversal> > public> static> void> printInorder(Node node)> > {> > if> (node ==> null> )> > return> ;> > // First recur on left subtree> > printInorder(node.left);> > // Now deal with the node> > Console.Write(node.data +> ' '> );> > // Then recur on right subtree> > printInorder(node.right);> > }> > // Driver code> > public> static> void> Main()> > {> > Node root => new> Node(1);> > root.left => new> Node(2);> > root.right => new> Node(3);> > root.left.left => new> Node(4);> > root.left.right => new> Node(5);> > root.right.right => new> Node(6);> > // Function call> > Console.WriteLine(> > 'Inorder traversal of binary tree is: '> );> > printInorder(root);> > }> }>

Javascript

// JavaScript program for inorder traversals> // Structure of a Binary Tree Node> class Node {> > constructor(v) {> > this> .data = v;> > this> .left => null> ;> > this> .right => null> ;> > }> }> // Function to print inorder traversal> function> printInorder(node) {> > if> (node ===> null> ) {> > return> ;> > }> > > // First recur on left subtree> > printInorder(node.left);> > > // Now deal with the node> > console.log(node.data);> > > // Then recur on right subtree> > printInorder(node.right);> }> // Driver code> const root => new> Node(1);> root.left => new> Node(2);> root.right => new> Node(3);> root.left.left => new> Node(4);> root.left.right => new> Node(5);> root.right.right => new> Node(6);> // Function call> console.log(> 'Inorder traversal of binary tree is: '> );> printInorder(root);>

Uitvoer

Inorder traversal of binary tree is: 4 2 5 1 3 6

Uitleg:

Hoe inorder traversal werkt

Complexiteitsanalyse:

Tijdcomplexiteit: O(N) waarbij N het totale aantal knooppunten is. Omdat het alle knooppunten minstens één keer doorkruist.
Hulpruimte: O(1) als er geen rekening wordt gehouden met recursiestapelruimte. Anders is O(h) waarbij h de hoogte van de boom is

In het slechtste geval, H kan hetzelfde zijn als N (als de boom een scheve boom is)
In het beste geval, H kan hetzelfde zijn als kalm (als de boom een complete boom is)

Gebruiksscenario's van Inorder Traversal:

In het geval van BST (Binary Search Tree), als het nodig is om de knooppunten in een niet-aflopende volgorde te krijgen, is de beste manier om een in-order-traversal te implementeren.

Gerelateerde artikelen: