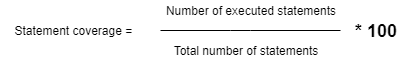TRIE DATU STRUKTŪRA | IEVIETOŠANA UN MEKLĒŠANA

The Izmēģiniet datu struktūru ir kokam līdzīga datu struktūra, ko izmanto dinamiskas virkņu kopas glabāšanai. To parasti izmanto efektīvai izguve un uzglabāšana atslēgām lielā datu kopā. Struktūra atbalsta tādas darbības kā ievietošana , Meklēt , un dzēšana atslēgām, padarot to par vērtīgu rīku tādās jomās kā datorzinātne un informācijas izguve. Šajā rakstā mēs izpētīsim ievietošana un meklēšana darbība Trie datu struktūrā.

Izmēģiniet datu struktūru

Satura rādītājs

Trie mezgla attēlojums
Trie mezgla attēlojums:
A Izmēģiniet datu struktūru sastāv no mezgliem, kas savienoti ar malām. Katrs mezgls apzīmē rakstzīmi vai virknes daļu. Saknes mezgls, Trie sākuma punkts, ir tukša virkne. Katra mala, kas nāk no mezgla, apzīmē noteiktu rakstzīmi. Ceļš no saknes uz mezglu apzīmē Trie saglabātās virknes prefiksu.

Vienkārša struktūra, kas attēlo angļu alfabēta mezglus, var būt šāda.
C++ struct TrieNode { // pointer array for child nodes of each node TrieNode* childNode[26]; // Used for indicating ending of string bool wordEnd; TrieNode() { // constructor // initialize the wordEnd variable with false // initialize every index of childNode array with // NULL wordEnd = false; for (int i = 0; i < 26; i++) { childNode[i] = NULL; } } };Java public class TrieNode { // Array for child nodes of each node TrieNode[] childNode; // Used for indicating the end of a string boolean wordEnd; // Constructor public TrieNode() { // Initialize the wordEnd variable with false wordEnd = false; // Initialize every index of the childNode array with null childNode = new TrieNode[26]; for (int i = 0; i < 26; i++) { childNode[i] = null; } } }
Apskatīsim vārdu ievietošanas procesu Trie datu struktūrā. Mēs jau esam apskatījuši Trie pamatus un tā mezglu struktūru.

Šeit ir vārdu ievietošanas vizuāls attēlojums un un ieslēgts Trie datu struktūrā:
Ievietot operāciju Trie datu struktūrā

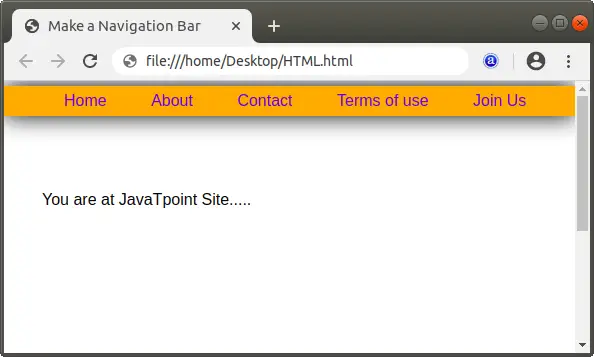
Ievietošana un Trie datu struktūra:
- Sāciet ar saknes mezglu: Saknes mezglam nav ar to un tā saistīta rakstzīme vārda beigas vērtība ir 0 , kas norāda, ka šajā brīdī pilns vārds nebeidzas.
- Pirmā rakstzīme a: Aprēķiniet indeksu, izmantojot ' a' - 'a' = 0 . Pārbaudiet, vai bērnsNode[0] ir null . Tā kā tas ir, izveidojiet jaunu TrieNode ar rakstzīmi a , vārda beigas iestatīts uz 0 un tukšu rādītāju masīvu. Pārvietojieties uz šo jauno mezglu.
- Otrā rakstzīme n: Aprēķiniet indeksu, izmantojot “n” — “a” = 13 . Pārbaudiet, vai bērnsNode[13] ir null . Tā ir, tāpēc izveidojiet jaunu TrieNode ar rakstzīmi n , vārda beigas iestatīts uz 0 un tukšu rādītāju masīvu. Pārvietojieties uz šo jauno mezglu.
- Trešā rakstzīme d: Aprēķiniet indeksu, izmantojot ' d' — 'a' = 3 . Pārbaudiet, vai bērnsNode[3 ] ir null . Tā ir, tāpēc izveidojiet jaunu TrieNode ar rakstzīmi d , vārda beigas iestatīts uz 1 (norādot vārdu un beidzas šeit).
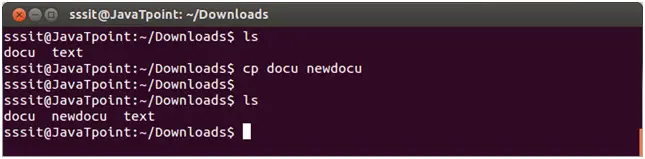
Skudras ievietošana Trie datu struktūrā:
- Sāciet ar saknes mezglu: Saknes mezglā nav datu, taču tas seko katras ievietotās virknes katrai pirmajai rakstzīmei.
- Pirmā rakstzīme a: Aprēķiniet indeksu, izmantojot ' a' - 'a' = 0 . Pārbaudiet, vai bērnsNode[0] ir null . Mums jau ir a mezgls, kas izveidots no iepriekšējās ievietošanas. tāpēc pāriet uz esošo a mezgls.
- Pirmā rakstzīme n: Aprēķiniet indeksu, izmantojot ' n — 'a' = 13 . Pārbaudiet, vai bērnsNode [13] ir null . Tā nav, tāpēc pārejiet uz esošo n mezgls.
- Otrā rakstzīme t: Aprēķiniet indeksu, izmantojot “t” — “a” = 19 . Pārbaudiet, vai bērnsNode [19] ir null . Tā ir, tāpēc izveidojiet jaunu TrieNode ar rakstzīmi t , vārda beigas iestatīts uz 1 (norādot, ka vārds skudra beidzas šeit).
Tālāk ir parādīta virkņu ievietošanas ieviešana Trie datu struktūrā:
C++ #include using namespace std; struct TrieNode { // pointer array for child nodes of each node TrieNode* childNode[26]; // Used for indicating ending of string bool wordEnd; TrieNode() { // constructor // initialize the wordEnd variable with false // initialize every index of childNode array with // NULL wordEnd = false; for (int i = 0; i < 26; i++) { childNode[i] = NULL; } } }; void insert_key(TrieNode* root, string& key) { // Initialize the currentNode pointer // with the root node TrieNode* currentNode = root; // Iterate across the length of the string for (auto c : key) { // Check if the node exist for the current // character in the Trie. if (currentNode->childNode[c - 'a'] == NULL) { // Ja mezgls pašreizējai rakstzīmei neeksistē // tad izveidojiet jaunu mezglu TrieNode* newNode = new TrieNode(); // Saglabājiet atsauci uz jaunizveidoto // mezglu. currentNode->childNode[c - 'a'] = jaunsMezgls; } // Tagad pārvietojiet pašreizējā mezgla rādītāju uz jaunizveidoto mezglu //. pašreizējaisNode = pašreizējaisNode->bērnmezgls[c - 'a']; } // Palieliniet wordEndCount pēdējam currentNode // rādītājam, tas nozīmē, ka ir virkne, kas beidzas ar // currentNode. pašreizējaisNode->wordEnd = 1; }
Laika sarežģītība: O(vārdu skaits * maxLengthOfWord)
Palīgtelpa: O(vārdu skaits * maxLengthOfWord)
Atslēgas meklēšana Trie datu struktūrā ir līdzīga tās ievietošanas darbībai. Tomēr Tas tikai salīdzina rakstzīmes un virzās uz leju . Meklēšana var beigties virknes beigu vai atslēgas trūkuma dēļ mēģinājumā.

Soli pa solim pieeja meklēšanai Trie Data struktūrā:
- Sāciet ar saknes mezglu. Tas ir sākumpunkts visiem meklējumiem Trie.
- Pārejiet pa Trie, pamatojoties uz meklētā vārda rakstzīmēm. Katrai rakstzīmei izpildiet atbilstošo zaru Trie. Ja filiāle neeksistē, vārda Trie nav.
- Ja sasniedzat vārda beigas un vārda beigas karodziņš ir iestatīts uz 1, vārds ir atrasts.
- Ja sasniedzat vārda beigas un vārda beigas karodziņš ir 0, vārda Trie nav, lai gan tam ir kopīgs prefikss ar esošu vārdu.
Šeit ir vizuāls meklēšanas vārda attēlojums tētis Trie datu struktūrā:
Pieņemsim, ka esam veiksmīgi ievietojuši vārdus un , ieslēgts , un tētis mūsu Trie, un mums ir jāmeklē konkrēti vārdi Trie datu struktūrā. Mēģināsim meklēt vārdu tētis :

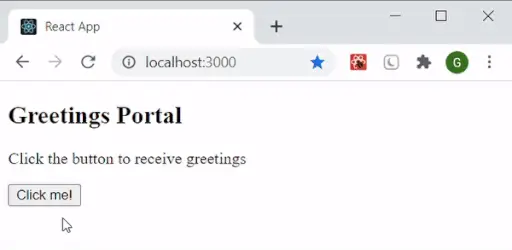
Meklēšanas darbība Trie datu struktūrā
- Mēs sākam no saknes mezgla.
- Mēs sekojam zaram, kas atbilst rakstzīmei “d”.
- Mēs sekojam zaram, kas atbilst rakstzīmei a’.
- Mēs sekojam zaram, kas atbilst rakstzīmei “d”.
- Mēs sasniedzam vārda beigas un vārda beigas karogs ir 1 . Tas nozīmē ka tētis ir klāt Trie.
Tālāk ir norādīta meklēšanas virkņu ieviešana Trie Data Structure:
C++ #include using namespace std; struct TrieNode { // pointer array for child nodes of each node TrieNode* childNode[26]; // Used for indicating ending of string bool wordEnd; TrieNode() { // constructor // initialize the wordEnd variable with false // initialize every index of childNode array with // NULL wordEnd = false; for (int i = 0; i < 26; i++) { childNode[i] = NULL; } } }; bool search_key(TrieNode* root, string& key) { // Initialize the currentNode pointer // with the root node TrieNode* currentNode = root; // Iterate across the length of the string for (auto c : key) { // Check if the node exist for the current // character in the Trie. if (currentNode->childNode[c - 'a'] == NULL) { // Dotais vārds neeksistē Trie return false; } // Pārvietojiet currentNode rādītāju uz jau esošo // esošās rakstzīmes mezglu. pašreizējaisNode = pašreizējaisNode->bērnmezgls[c - 'a']; } return (currentNode->wordEnd == true); }
Laika sarežģītība: O(vārdu skaits * maxLengthOfWord)
Palīgtelpa: O(vārdu skaits * maxLengthOfWord)
Izveidojiet saknes mezglu ar palīdzību TrieNode() konstruktors.
Saglabājiet virkņu kolekciju, kas jāievieto trie, virkņu vektorā, piemēram, arr .
Visu virkņu ievietošana Trie ar palīdzību insert_key() funkcija,
Meklēt virknes ar palīdzību search_key() funkciju.

Tālāk ir aprakstīta iepriekš minētās pieejas īstenošana.

C++

  #include  using namespace std; struct TrieNode {  // pointer array for child nodes of each node  TrieNode* childNode[26];  // Used for indicating ending of string  bool wordEnd;  TrieNode()  {  // constructor  // initialize the wordEnd variable with false  // initialize every index of childNode array with  // NULL  wordEnd = false;  for (int i = 0; i  < 26; i++) {  childNode[i] = NULL;  }  } }; void insert_key(TrieNode* root, string& key) {  // Initialize the currentNode pointer  // with the root node  TrieNode* currentNode = root;  // Iterate across the length of the string  for (auto c : key) {  // Check if the node exist for the current  // character in the Trie.  if (currentNode->childNode[c - 'a'] == NULL) { // Ja mezgls pašreizējai rakstzīmei neeksistē // tad izveidojiet jaunu mezglu TrieNode* newNode = new TrieNode();  // Saglabājiet atsauci uz jaunizveidoto // mezglu.  currentNode->childNode[c - 'a'] = jaunsMezgls;  } // Tagad pārvietojiet pašreizējā mezgla rādītāju uz jaunizveidoto mezglu //.  pašreizējaisNode = pašreizējaisNode->bērnmezgls[c - 'a'];  } // Palieliniet wordEndCount pēdējam currentNode // rādītājam, tas nozīmē, ka ir virkne, kas beidzas ar // currentNode.  pašreizējaisNode->wordEnd = 1; } bool search_key(TrieNode* root, string& key) { // Inicializēt currentNode rādītāju // ar saknes mezglu TrieNode* currentNode = root;  // Atkārtojiet visā virknes garumā (auto c : taustiņš) { // Pārbaudiet, vai Trie pašreizējai // rakstzīmei eksistē mezgls.  if (currentNode->childNode[c - 'a'] == NULL) { // Dotais vārds Trie neeksistē return false;  } // Pārvietojiet currentNode rādītāju uz jau esošo // esošās rakstzīmes mezglu.  pašreizējaisNode = pašreizējaisNode->bērnmezgls[c - 'a'];  } return (currentNode->wordEnd == true); } // Draivera kods int main() { // Izveidojiet Trie TrieNode saknes mezglu* root = new TrieNode();  // Saglabā virknes, kuras vēlamies ievietot // Trie vektorā inputStrings = { 'un', 'ant', 'do', 'geek', 'tētis', 'bumba'};  // ievietošanas operāciju skaits laukā Trie int n = inputStrings.size();  for (int i = 0; i < n; i++) {  insert_key(root, inputStrings[i]);  }  // Stores the strings that we want to search in the Trie  vector searchQueryStrings = { 'do', 'geek', 'bat' };  // meklēšanas operāciju skaits laukā Izmēģiniet int searchQueries = searchQueryStrings.size();  for (int i = 0; i < searchQueries; i++) {  cout  < < 'Query String: '  < < searchQueryStrings[i]   < < '
';  if (search_key(root, searchQueryStrings[i])) {  // the queryString is present in the Trie  cout  < < 'The query string is present in the '  'Trie
';  }  else {  // the queryString is not present in the Trie  cout  < < 'The query string is not present in '  'the Trie
';  }  }  return 0; }

Java

  class TrieNode {  TrieNode[] childNode;  boolean wordEnd;  TrieNode()  {  childNode = new TrieNode[26];  wordEnd = false;  } } class Trie {  TrieNode root;  Trie() { root = new TrieNode(); }  // Function to insert a key into the Trie  void insert(String key)  {  TrieNode currentNode = root;  for (int i = 0; i  < key.length(); i++) {  int index = key.charAt(i) - 'a';  if (currentNode.childNode[index] == null) {  currentNode.childNode[index]  = new TrieNode();  }  currentNode = currentNode.childNode[index];  }  currentNode.wordEnd = true;  }  // Function to search for a key in the Trie  boolean search(String key)  {  TrieNode currentNode = root;  for (int i = 0; i  < key.length(); i++) {  int index = key.charAt(i) - 'a';  if (currentNode.childNode[index] == null) {  return false;  }  currentNode = currentNode.childNode[index];  }  return currentNode.wordEnd;  } } public class Main {  public static void main(String[] args)  {  Trie trie = new Trie();  String[] inputStrings  = { 'and', 'ant', 'do', 'geek', 'dad', 'ball' };  // Insert each string into the Trie  for (String str : inputStrings) {  trie.insert(str);  }  String[] searchQueryStrings  = { 'do', 'geek', 'bat' };  // Search for each string and print whether it is  // found in the Trie  for (String query : searchQueryStrings) {  System.out.println('Query String: ' + query);  if (trie.search(query)) {  System.out.println(  'The query string is present in the Trie');  }  else {  System.out.println(  'The query string is not present in the Trie');  }  }  } }

Python

  class TrieNode: def __init__(self): self.childNode = [None] * 26 self.wordEnd = False class Trie: def __init__(self): self.root = TrieNode() # Function to insert a key into the Trie def insert(self, key): currentNode = self.root for char in key: index = ord(char) - ord('a') if not currentNode.childNode[index]: currentNode.childNode[index] = TrieNode() currentNode = currentNode.childNode[index] currentNode.wordEnd = True # Function to search for a key in the Trie def search(self, key): currentNode = self.root for char in key: index = ord(char) - ord('a') if not currentNode.childNode[index]: return False currentNode = currentNode.childNode[index] return currentNode.wordEnd if __name__ == '__main__': trie = Trie() inputStrings = ['and', 'ant', 'do', 'geek', 'dad', 'ball'] # Insert each string into the Trie for word in inputStrings: trie.insert(word) searchQueryStrings = ['do', 'geek', 'bat'] # Search for each string and print whether it is found in the Trie for query in searchQueryStrings: print('Query String:', query) if trie.search(query): print('The query string is present in the Trie') else: print('The query string is not present in the Trie')

JavaScript

class TrieNode {  constructor() {  // Initialize the childNode array with 26 nulls  this.childNode = Array(26).fill(null);  // Initialize wordEnd to the false indicating that no word ends here yet  this.wordEnd = false;  } } class Trie {  constructor() {  // Initialize the root node of the Trie  this.root = new TrieNode();  }  // Function to insert a key into the Trie  insert(key) {  // Start from the root node  let currentNode = this.root;  for (let i = 0; i  < key.length; i++) {  const index = key.charCodeAt(i) - 'a'.charCodeAt(0);  if (currentNode.childNode[index] === null) {  currentNode.childNode[index] = new TrieNode();  }  // Move to the next node in the Trie  currentNode = currentNode.childNode[index];  }  // Mark the end of the word  currentNode.wordEnd = true;  }  // Function to search for a key in the Trie  search(key) {  // Start from the root node  let currentNode = this.root;  // Iterate through each character in the key  for (let i = 0; i  < key.length; i++) {  const index = key.charCodeAt(i) - 'a'.charCodeAt(0);  if (currentNode.childNode[index] === null) {  return false;  }  // Move to the next node in the Trie  currentNode = currentNode.childNode[index];  }  // Return true if the end of the word is marked otherwise false  return currentNode.wordEnd;  } } // Driver code const trie = new Trie(); const inputStrings = ['and', 'ant', 'do', 'geek', 'dad', 'ball']; // Insert each string into the Trie inputStrings.forEach((str) =>trie.insert(str)); const searchQueryStrings = ['do', 'geek', 'bat']; // Meklējiet katru virkni un izdrukājiet, vai tā ir atrodama laukā Trie searchQueryStrings.forEach((query) => { console.log(`Query String: ${query}`); if (trie.search(query)) { console.log('Vaicājuma virkne ir klāt Trie' } else { console.log('Vaicājuma virkne nav atrodama Trie'});>>   
  Izvade       Saistītie raksti:        
      Mēģiniet dzēst    
      Tiek rādīts Trie saturs    
       Automātiskās pabeigšanas funkcija, izmantojot Trie    
    Rakstu meklēšana, izmantojot visu sufiksu izmēģināšanu    
      Prakses problēmas:      
      Minimālais vārdu pārtraukums   
   Unikālas rindas binārā matricā   
   Atšķirīgu apakšvirkņu skaits   
   Vārdu satraukums   
   Virkņu (vai vārdu) masīva kārtošana, izmantojot Trie