Sapludināšanas kārtošanas laika un telpas sarežģītības analīze
The Laika sarežģītība no sapludināšanas kārtošanas ir O(n log n) abās vidēji un sliktākie gadījumi . Telpas sarežģītība Sapludināt kārtošanu ir O(n) . 
| Aspekts | Sarežģītība |
|---|---|
| Laika sarežģītība | O(n log n) |
| Kosmosa sarežģītība | O(n) |
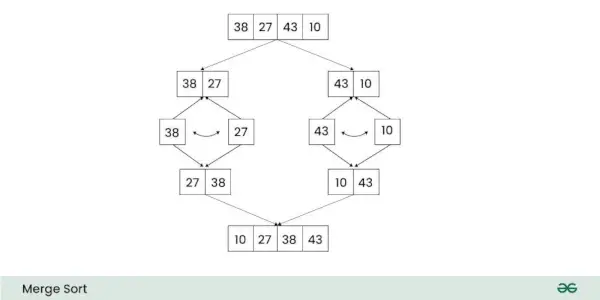
Sapludināšanas kārtošanas laika sarežģītības analīze:
Apsveriet šādu terminoloģiju:
T(k) = laiks, kas nepieciešams k elementu kārtošanai
M(k) = laiks, kas nepieciešams k elementu sapludināšanai
Tātad, tā var uzrakstīt
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + konstante * N
Šie N/2 elementi ir sadalīti divās daļās. Tātad,
T(N) = 2 * [2 * T(N/4) + konstante * N/2] + konstante * N
= 4 * T(N/4) + 2 * N * konstante
. . .
= 2 k * T(N/2 k ) + k * N * konstante
To var sadalīt maksimāli, līdz paliek viens elements. Tātad, tad N/2 k = 1. k = log 2 N
T(N) = N * T(1) + N * log 2 N * konstante
= N + N * log 2 N
Tāpēc laika sarežģītība ir O(N * log 2 N) .
Tātad labākajā, sliktākajā un vidējā gadījumā laika sarežģītība ir vienāda.
Telpas sarežģītības analīze sapludināšanas kārtošanai:
Apvienot kārtošanu ir telpas sarežģītība no O(n) . Tas ir tāpēc, ka tas izmanto papildu izmēru masīvu n lai sapludinātu ievades masīva sakārtotās puses. Papildu masīvs tiek izmantots, lai saglabātu apvienoto rezultātu, un ievades masīvs tiek pārrakstīts ar sakārtoto rezultātu.