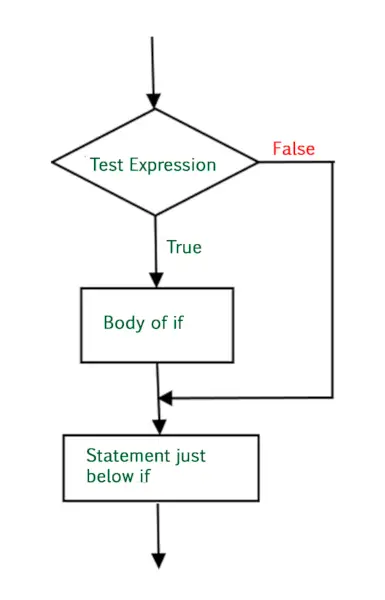
PYTHON PROGRAMMA BINĀRAJAI MEKLĒŠANAI (REKURSĪVAI UN ITERATĪVAI) — TECHCODEVIEW.COM

Īsumā, šis meklēšanas algoritms izmanto elementu kolekcijas priekšrocības, kas jau ir sakārtotas, ignorējot pusi elementu tikai pēc viena salīdzinājuma.

Salīdziniet x ar vidējo elementu.
Ja x sakrīt ar vidējo elementu, mēs atgriežam vidējo indeksu.
Citādi, ja x ir lielāks par vidējo elementu, tad x var atrasties tikai labajā (lielākajā) apakšgrupā aiz vidus elementa. Tad mēs atkal piemērojam algoritmu labajai pusei.
Ja x ir mazāks, mērķim x jāatrodas kreisajā (apakšējā) pusē. Tātad mēs izmantojam algoritmu kreisajai pusei.

Python programma binārajai meklēšanai, izmantojot rekursīvu

Python3

# Python 3 program for recursive binary search.> # Modifications needed for the older Python 2 are found in comments.> # Returns index of x in arr if present, else -1> def> binary_search(arr, low, high, x):> > # Check base case> > if> high>>> ,> str> (result))> else> :> > print> (> 'Element is not present in array'> )>

Izvade

Element is present at index 3

Laika sarežģītība : O(log n)

Palīgtelpa : O(pieteikties) [PIEZĪME: Rekursija izveido zvanu steku]

Python programma binārajai meklēšanai, izmantojot iteratīvu

Python3

# Iterative Binary Search Function> # It returns index of x in given array arr if present,> # else returns -1> def> binary_search(arr, x):> > low> => 0> > high> => len> (arr)> -> 1> > mid> => 0> > while> low <> => high:> > mid> => (high> +> low)> /> /> 2> > # If x is greater, ignore left half> > if>

arr[mid]   low = mid + 1  # If x is smaller, ignore right half  elif arr[mid]>x: high = mid - 1 # nozīmē x ir vidum else: return mid # Ja mēs sasniedzam šeit, tad elements neatradās return -1 # Testa masīvs arr = [ 2, 3, 4, 10, 40 ] x = 10 # Funkcijas izsaukuma rezultāts = binary_search(arr, x) if rezultāts != -1: print('Elements atrodas indeksā', str(rezultāts)) else: print('Elements nav masīvā ')>>

>    
      
      Palīgtelpa     : O(1)  
      Python programma binārajai meklēšanai, izmantojot iebūvēto bisect moduli     
      Soli pa solim pieeja:     
     Kods importē bisect moduli, kas nodrošina atbalstu binārajai meklēšanai.  
   Ir definēta funkcija binary_search_bisect(), kas kā ievadi izmanto masīvu arr un elementu, lai meklētu x.  
   Funkcija izsauc bisect_left() funkciju bisect modulim, kas atrod elementa pozīciju sakārtotajā masīvā arr, kur x jāievieto, lai saglabātu sakārtoto secību. Ja elements jau atrodas masīvā, šī funkcija atgriezīs savu pozīciju.  
   Pēc tam funkcija pārbauda, vai atgrieztais indekss i atrodas masīva diapazonā un vai šī indeksa elements ir vienāds ar x.  
   Ja nosacījums ir patiess, funkcija atgriež indeksu i kā elementa pozīciju masīvā.  
   Ja nosacījums ir nepatiess, funkcija atgriež -1, norādot, ka elements masīvā nav.  
   Pēc tam kods definē masīvu arr un elementu x, ko meklēt.  
   Funkcija binary_search_bisect() tiek izsaukta ar arr un x kā ievadi, un atgrieztais rezultāts tiek saglabāts rezultāta mainīgajā.  
   Pēc tam kods pārbauda, vai rezultāts nav vienāds ar -1, norādot, ka elements atrodas masīvā. Ja patiess, tas izdrukā elementa pozīciju masīvā.  
   Ja rezultāts ir vienāds ar -1, kods izdrukā ziņojumu, ka elements masīvā nav.  
  
  Python3 
      
       
   
       
       
     
     
   
          import>   bisect>   >   def>   binary_search_bisect(arr, x):>   >  i>  =>   bisect.bisect_left(arr, x)>   >  if>   i !>  =>   len>  (arr)>  and>   arr[i]>  =>  =>   x:>   >  return>   i>   >  else>  :>   >  return>   ->  1>   >   >   # Test array>   arr>  =>   [>  2>  ,>  3>  ,>  4>  ,>  10>  ,>  40>  ]>   x>  =>   10>   >   # Function call>   result>  =>   binary_search_bisect(arr, x)>   >   if>   result !>  =>   ->  1>  :>   >  print>  (>  'Element is present at index'>  ,>  str>  (result))>   else>  :>   >  print>  (>  'Element is not present in array'>  )>     
  
  
   
      
    
      
    
  Izvade    
  Element is present at index 3 
      Laika sarežģītība     : O(log n)  
      Palīgtelpa     : O(1)